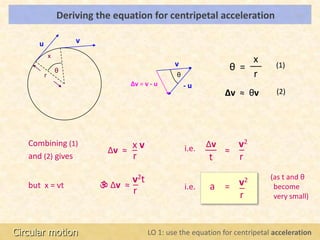
This document provides an overview of a physics lesson on centripetal force and acceleration. It introduces the key equations for centripetal acceleration (a = v2/r) and centripetal force (F = mv2/r). The learning objectives are to use these two equations and solve basic problems using them. The document then derives the equations step-by-step, showing the relationship between centripetal acceleration and the change in velocity of an object moving in circular motion.

1. A-level Physics
Unit G484:
The Newtonian
World
Centripetal force &
acceleration
Circular motion

2. Lesson focus
• Centripetal acceleration and force
Learning objectives
At the end of the lesson you will be able to:
• use the equation for centripetal acceleration a = v2/r ;
• use the equation for centripetal force F = ma = mv2/r .
Circular motion

3. Learning outcomes
All of you should be able to
• recall the equation for centripetal acceleration;
• recall the equation for centripetal force;
• solve basic problems using these equations.
Most of you will be able to
• solve more complex problems using these equations.
Circular motion

4. Deriving the equation for centripetal acceleration LOs
u v
x
x - arc length
θ x
r
θ = (1) r - radius
r
θ - angle (in radians)
subtended by
arc length x
v
θ Δv (2)
Δv = v - u θ ≈ i.e. Δv ≈ θv
-u v
Circular motion LO 1: use the equation for centripetal acceleration

5. Deriving the equation for centripetal acceleration LOs
u v
x
v x (1)
θ θ =
r θ r
Δv = v - u -u
Δv ≈ θv (2)
Combining (1) xv i.e. Δv v2
Δv ≈ ≈
and (2) gives r t r
v2t (as t and θ
but x = vt  Δv ≈ i.e. a = v2 become
r r very small)
Circular motion LO 1: use the equation for centripetal acceleration

6. Deriving the equation for centripetal acceleration LOs
u v
x
v
θ
r θ
Δv = v - u -u
a = v2
r
 F = mv2 since F = ma
r
Circular motion LO 1: use the equation for centripetal acceleration