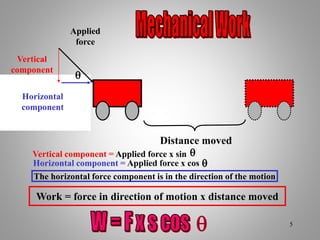
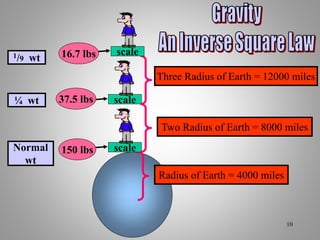
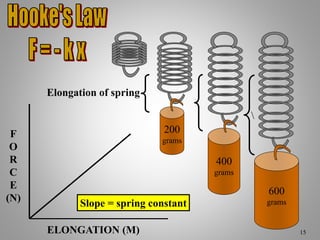
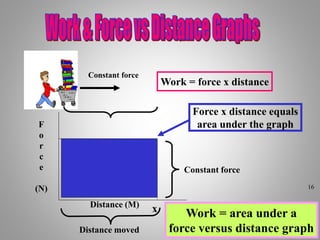
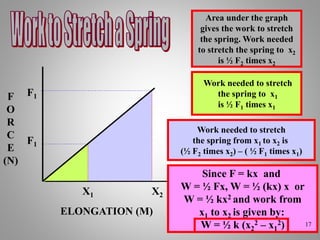
The document provides an overview of work and energy in physics, defining work as the product of force and distance moved in the direction of the applied force. It explains different types of mechanical energy, including gravitational potential energy, kinetic energy, and elastic potential energy, along with their formulas. Additionally, it covers the concept of measuring energy relative to gravitational fields and different conditions affecting the work done.

1. Copyright Sautter 2015

2. WORK & ENERGY
• Work, in a physics sense, has a precise definition,
unlike the common use of the word. When you do
your home “work” you probably, from a physics stand
point, did no work at all !
• Work is defined as force applied in the direction of the
motion multiplied times the distance moved.
• When work is done by moving an object in a
horizontal direction, work equals the applied force
times the cosine of the angle of the applied force times
the distance the object is moved.
• W = F (cos ) x s, (s stands for distance)
• Work is a scalar quantity (it has no direction). The
sign of a work quantity (positive or negative) indicates
the direction of energy flow as into or out of a system
but does not give it a direction as in a vector quantity.
2

3. 3

4. WORK & ENERGY
• The terms work and energy are interchangeable.
Energy is defined as the ability to do work.
• Kinds of work and energy
• (1) mechanical work – work done by applying a
force over a distance
• (2) work of friction – work required to overcome
friction
• (3) gravitational potential energy – energy needed to
lift an object against the force of gravity
• (4) elastic potential energy – the energy stored in a
compressed or stretched spring
• (5) kinetic energy – energy an object has because of
its motion (velocity)
4

5. Distance moved
Applied
force
Vertical
component
Horizontal
component

Vertical component = Applied force x sin 
Horizontal component = Applied force x cos 

Work = force in direction of motion x distance moved
The horizontal force component is in the direction of the motion
5

6. FORCE OF FRICTION = 0
WORK DONE = 0
FORCE OF FRICTION > 0
WORK DONE = FFRICTION x DISTANCE
Recall: Ffriction = coefficient of friction x Fnormal
and on a horizontal surface:
Fnormal = weight of object = mass x gravity
6

7. GRAVITATIONAL POTENTIAL ENERGY
• When an object is lifted, work is done against the
force of gravity (the weight of the object).
• Since weight is a force and the height to which an
object is lifted is a distance, then force times
distance equals work done.
• Weight of an object can be calculated using mass
time gravity. When objects are lifted near the
surface of the earth, gravity is assumed to be
constant at 9.8 m/s2 (32 ft/s2).
• If object are lifted well beyond the earth’s surface
gravity diminishes to progressively smaller values
and the work done in the lifting becomes less and
less. 7

8. GRAVITATIONAL POTENTIAL ENERGY
• Potential energy change equals weight times
change in height.
• Weight equals mass times gravity
• Potential energy change equals mass times
gravity times height (distance lifted)
 
8

9. MEASUREMENT OF POTENTIAL ENERGY IS RELATIVE
Boy Two!
You’re at a
High potential
I sure am !
Who are they
kidding ??
One
Two
Three
Two is at a higher potential
energy than One but lower than
Three. Two’s potential energy is
negative relative to Three’s and
positive relative to One’s.
If this point was used as reference,
One, Two and Three would all have
negative potential energies.
9

10. Radius of Earth = 4000 miles
scale150 lbs
Two Radius of Earth = 8000 miles
scale37.5 lbs
Three Radius of Earth = 12000 miles
scale16.7 lbs
¼ wt
1/9 wt
Normal
wt
10

11. Calculating Work in Different
Gravitational Fields
• Potential energy changes are different in different gravitational
field because the value of g changes.
• As seen in the previous slide, at an altitude of one earth radii
above the earth (4000 miles) gravity is ¼ of normal gravity (1/4 x
9.8 m/s2 = 2.45 m/s2). At two earth radii altitude, gravity is 1.09
m/s2.
• An object of mass 10 kg is lifted 5 meters on earth. The work done
(potential energy increase) is (P.E. = mgh) 10 kg x 9.8 m/s2 x 5 m =
490 joules.
• At one earth radii, work done is 10 kg x 2.45 m/s2 x 5 m = 122.5
joules (1/4 of the work done in lifting the same object on earth)
• At two earth radii above the earth (8000 miles altitude) the work
done on the same object is 10 kg x 1.09 m/s2 x 5 m = 54.4 joules
(1/9 of the work required to lift the object on earth)
11

12. KINETIC ENERGY
• Kinetic energy is the energy of motion. In order to possess
kinetic energy an object must be moving.
• As the speed (velocity) of an object increases its kinetic energy
increases. The kinetic energy content of a body is also related to
its mass. The most massive objects at the same speed contain the
most kinetic energy.
• Work = force x distance (W = F x s )
• Recall that F = mass x acceleration (F = m x a)
• Therefore: Work = m x a x s
• Also, for an object initially at rest, recall that acceleration equals
the final velocity squared divided by twice the distance traveled:
a = v2 / (2 s)
• Work = m (v2 / (2 s)) s, canceling out the distance term (s) gives,
Work = (m v2 ) / 2 or 1/2 m v2
• Since the object is in motion, the work content is called kinetic
energy and therefore: K.E. = 1/2 m v2 12

13. High kinetic energy.
High velocity !
Kinetic energy = 0
No motion !
13

14. ELASTIC POTENTIAL ENERGY
• Elastic potential energy refers to the energy which is stored
in stretched of compressed items such as springs or rubber
bands.
• The elongation or compression of elastic bodies is described
by Hooke’s Law. This law relates the force applied to the
elongation or compression experienced by the body.
• In plain words, Hooke’s Law says, “the harder you pull on a
spring, the more it stretches”. This relationship is given by
the equation: F = k x.
• F is the applied force, k is a constant called the spring
constant or Hooke’s constant and x is the elongation of the
spring.
• Springs with large k values are hard to stretch or compress
such as a car spring. Those with small constants are easy of
stretch or compress such as a slinky spring. 14

15. 400
grams
200
grams
F
O
R
C
E
(N)
ELONGATION (M)
Slope = spring constant
600
grams
Elongation of spring
15

16. F
o
r
c
e
(N)
Distance (M)
x
Constant force
Work = force x distance
Constant force
Distance moved
Force x distance equals
area under the graph
Work = area under a
force versus distance graph
16

17. F
O
R
C
E
(N)
ELONGATION (M)
X1 X2
F1
F1
Area under the graph
gives the work to stretch
the spring. Work needed
to stretch the spring to x2
is ½ F2 times x2
Work needed to stretch
the spring to x1
is ½ F1 times x1
Work needed to stretch
the spring from x1 to x2 is
(½ F2 times x2) – ( ½ F1 times x1)
Since F = kx and
W = ½ Fx, W = ½ (kx) x or
W = ½ kx2 and work from
x1 to x2 is given by:
W = ½ k (x2
2 – x1
2) 17

18. 
18

19. F
O
R
C
E
(N)
DISPLACEMENT (M)
X1 X2
WORK = AREA UNDER THE CURVE
W =  F  X (SUM OF THE BOXES)
WIDTH OF EACH BOX =  X
AREA MISSED - INCREASING
THE NUMBER BOXES WILL
REDUCE THIS ERROR!
AS THE NUMBER OF BOXES
INCREASES, THE ERROR
DECREASES!
BOX METHOD
19

20. Finding Area Under Curves Mathematically
• Areas under force versus distance graphs (work)
can be found mathematically. The process
requires that the equation for the graph be
known and integral calculus be used.
• Recall that integration is also referred to as
finding the antiderivative of a function.
• The next slide reviews the steps in finding the
integral of the basic function, y = kxn.
20

21. 21
Click Here