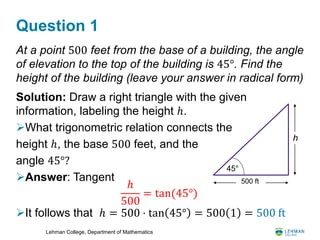
This document contains a 10 question review for a trigonometry midterm examination. It reviews concepts like using trigonometric functions to solve for unknown sides and angles of right triangles, evaluating trig functions for special angles, finding arc lengths and sector areas of circles, graphing trig functions involving amplitude, period and phase shift, and using trigonometric identities. The problems are worked out step-by-step showing the reasoning and math steps to arrive at the solutions, often leaving final answers in radical or pi form.

1. Trigonometry – MAT 108
Midterm Examination Review
Spring
2020

2. Lehman College, Department of Mathematics
Question 1
At a point 500 feet from the base of a building, the angle
of elevation to the top of the building is 45°. Find the
height of the building (leave your answer in radical form)
Solution: Draw a right triangle with the given
information, labeling the height ℎ.
What trigonometric relation connects the
height ℎ, the base 500 feet, and the
angle 45°?
Answer: Tangent
It follows that ℎ = 500 ⋅ tan 45° = 500 1 = 500 ft
h
500 ft
45°
ℎ
500
= tan(45°)

3. Lehman College, Department of Mathematics
Question 2 (1 of 2)
For the acute angle 𝜃, with cos 𝜃 = 1
3, use the
trigonometric identities only to determine the values
of: (a) sin 𝜃 and (b) tan 𝜃.
Solution: The Pythagorean trigonometric identity
sin2 𝜃 + cos2 𝜃 = 1 connects sin 𝜃 with cos 𝜃. It
follows that
sin2
𝜃 = 1 − cos2
𝜃
sin2
𝜃 = 1 − 1
3
2
sin2
𝜃 = 1 −
1
9
sin2
𝜃 = 9
9
− 1
9
=
8
9

4. Lehman College, Department of Mathematics
Question 2 (2 of 2)
Taking square roots of both sides, we obtain
Now that we know the values of sin 𝜃 and cos 𝜃,
what trigonometric identity connects tan 𝜃 to sin 𝜃
and cos 𝜃?
It follows that,
sin 𝜃 =
8
9
=
8
9
=
2 2
3
tan 𝜃 =
sin 𝜃
cos 𝜃
tan 𝜃 = sin 𝜃 ÷ cos 𝜃 =
2 2
3
÷
1
3
=
2 2
3
⋅
3
1
= 2 2

5. Lehman College, Department of Mathematics
Question 3(a)
Evaluate, without using a calculator, the sine, cosine
and tangent of: (a) 135°[5 points], and (b)
5𝜋
3
[5 points],
Solution: (a) Since 135° is greater than 90° but less
than 180° (quadrant II), its reference angle is given by:
It follows that
Note: You must use the reference angle method.
Above we used the fact that in quadrant II, sine is
positive and both cosine and tangent are negative. A
diagram may also be useful.
sin 135° = + sin 45° = 2
2
180° − 135° = 45°
cos 135° = − cos 45° = − 2
2
tan 135° = − tan 45° = −1

6. Lehman College, Department of Mathematics
Question 3(b)
Solution: (b) Since
5𝜋
3
is greater than
3𝜋
2
but less than 2𝜋
(quadrant IV), its reference angle is given by:
It follows that
Note: You must use the reference angle method. Above we
used the fact that in quadrant III, cosine is positive and both
sine and tangent are negative. A diagram may also be useful.
.
sin
5𝜋
3
= − sin
𝜋
3
= − 3
2
cos
5𝜋
3
= + cos
𝜋
3
= + 1
2
tan
5𝜋
3
= − tan
𝜋
3
= − 3
2𝜋 −
5𝜋
3
=
6𝜋
3
−
5𝜋
3
=
𝜋
3

7. Lehman College, Department of Mathematics
Question 4
If 𝑠𝑒𝑐 𝑥 = − 13
5, and 𝑥 is an angle in quadrant III, find the
values of the other five trigonometric functions.
Solution: Express the given information in terms of a more familiar
trigonometric function: cos 𝑥 =
1
sec 𝑥
= − 5
13 with 𝑥 in quadrant III. Next,
sketch a diagram of the situation. Where does the 13 go? What about the 5?
Answer: the 13 goes on the hypotenuse and the 5 on the adjacent.
 What is the length of the third side of the triangle?
Answer: 12 units. This is a 5-12-13 triangle.
 Now, compute the values of the other four
trigonometric functions, using the coordinates or ASTC:
sin 𝑥 = −
12
13
; csc 𝑥 = 1
sin 𝑥
= −
13
12
tan 𝑥 = 12
5
; cot 𝑥 = 1
tan 𝑥
=
5
12
13
5
12

8. Lehman College, Department of Mathematics
Question 5
(a) Find the length of the arc of a circle of radius 3 cm that
subtends a central angle of 150°[5 points]. (b) Determine the
area of the corresponding sector [5 points] (leave all
answers in terms of 𝜋).
Solution: (a) If 𝜃 is given in degrees, then the arc length 𝑙 is
given by the formula:
So,
(a) Area of sector 𝑆 is given by the formula:
It follows that
𝑙 =
𝜃
360°
⋅ 2𝜋𝑟
𝑙 =
150°
360°
⋅ 2𝜋 3 =
5
12
⋅ 6𝜋 =
5𝜋
2
cm
𝑆 =
𝜃
360°
⋅ 𝜋𝑟2
𝑆 =
150°
360°
⋅ 𝜋 3 2
=
5
12
⋅ 9𝜋 =
15𝜋
4
cm2

9. Lehman College, Department of Mathematics
Question 6
(a) Find the length of the arc of a circle of radius 3 cm
that subtends a central angle of
2𝜋
5
[5 points].
(b) Determine the area of the corresponding sector
[5 points] (leave all answers in terms of 𝜋).
Solution: (a) If 𝜃 is given in radians, then the arc length
𝑙 is given by the formula:
So
(a) Area of sector 𝑆 is given by the formula:
It follows that
𝑙 = 3
2𝜋
5
=
6𝜋
5
cm
𝑙 = 𝑟𝜃
𝑆 =
1
2
⋅
2𝜋
5
3 2
=
𝜋
5
9 =
9𝜋
5
cm2
𝑆 =
1
2
𝜃𝑟2

10. Lehman College, Department of Mathematics
Question 7 (1 of 2)
Determine the amplitude, period and phase shift of the
function y = 3 sin(2𝑥 −
𝜋
3
). Hence or otherwise, sketch
exactly one period of the graph of y = 3 sin(2𝑥 −
𝜋
3
).
Solution: Amplitude = 3 = 3. There is no reflection
over the x-axis. To determine the period and phase
shift, let
Add
𝜋
3
to each side of the above inequality:
Divide by 2
0 ≤ 2𝑥 −
𝜋
3
≤ 2𝜋
0 +
𝜋
3
≤ 2𝑥 ≤ 2𝜋 +
𝜋
3
𝜋
3
≤ 2𝑥 ≤
7𝜋
3
𝜋
6
≤ 𝑥 ≤
7𝜋
6

11. Lehman College, Department of Mathematics
Question 7 (2 of 2)
It follows that the phase shift =
𝜋
6
; the period =
7𝜋
6
−
𝜋
6
= 𝜋
Graph one period of the function y = sin(𝑥)
Finally, to graph the given function, put
𝜋
6
at the
position where 0 is on the sine graph and replace 2𝜋
by
7𝜋
6

12. Lehman College, Department of Mathematics
Question 8
In triangle ABC, side a = 7 in, side b = 4 in, and ∠C =
60°. Find the area of the triangle (leave your answer in
radical form) [10 points].
Solution: Draw a scalene triangle ABC and label the
vertices and side lengths as given in the problem.
The formula for the area of an SAS
triangle is
For the given problem: A
B
C
𝑎 = 7 in
𝑏 = 4 in
60°
𝐴𝑟𝑒𝑎 =
1
2
(7)(4) sin 60° = 14 3
2
= 7 3 in2
𝐴𝑟𝑒𝑎 =
1
2
𝑎𝑏 sin(∠C)

13. Lehman College, Department of Mathematics
Question 9 (1 of 2)
In triangle ABC, side a = 2 in, ∠𝐴 = 60°, and
∠𝐵 = 45°. Find the length of side b (leave your
answer in radical form) [10 points].
Solution: Draw a scalene triangle ABC and label
the vertices and side lengths as given in the
problem.
This is an application of the Rule of Sines:
A
B
C
𝑎 = 2 in
𝑏 = ?
60°
45°
𝑏
sin(∠𝐵)
=
𝑎
sin(∠𝐴)

14. Lehman College, Department of Mathematics
Question 9 (2 of 2)
For the given problem:
It follows that
Converting the division to multiplication by
reciprocal, we obtain:
𝑏
sin(45°)
=
2
sin(60°)
𝑏 =
2 ⋅ sin(45°)
sin(60°)
= 2 sin 45° ÷ sin(60°)
𝑏 =
2 2
3
3
3
=
2 6
3
in
= 2
2
2
÷
3
2
= 2 ⋅
2
3

15. Lehman College, Department of Mathematics
Question 10 (1 of 2)
In triangle ABC, side b = 4 in, side c = 5 in, and
∠𝐴 = 45°. Find the length of side a (leave your
answer in radical form).
Solution: Draw a scalene triangle ABC and label
the vertices and side lengths as given in the
problem.
This is an application of the Rule of Cosines:
A
B
C
𝑎 = ?
𝑏 = 4 in
45°
𝑐 = 5 in
𝑎2
= 𝑏2
+ 𝑐2
− 2𝑏𝑐 cos(∠𝐴)

16. Lehman College, Department of Mathematics
Question 10 (2 of 2)
For the given problem:
Taking square roots, we obtain:
Note: the answer cannot be simplified further.
𝑎2 = 42 + 52 − 2(4)(5) cos(45°)
𝑎2 = 16 + 25 − 2(20)
2
2
𝑎2
= 41 − 20 2
𝑎 = 41 − 20 2 in