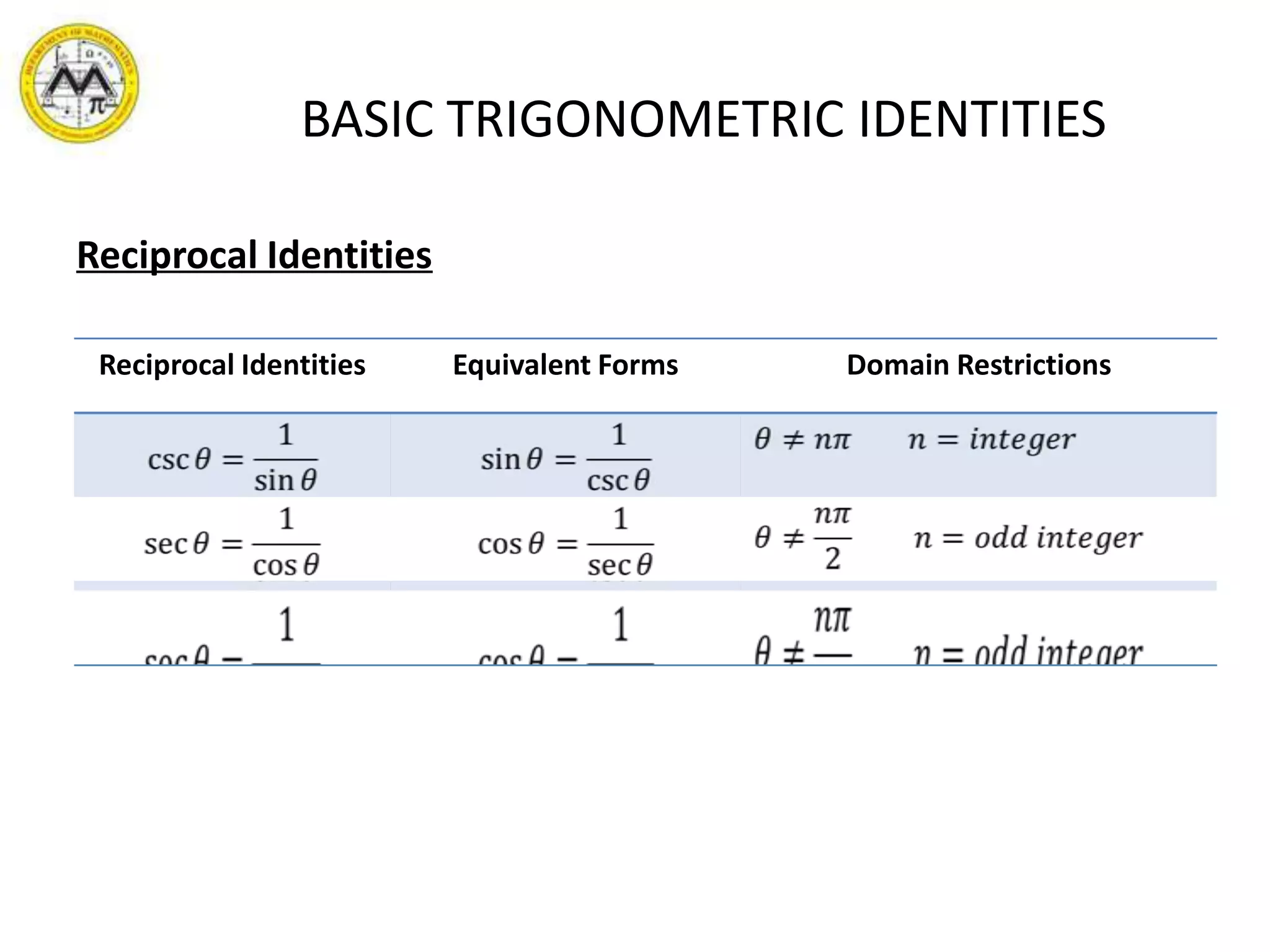
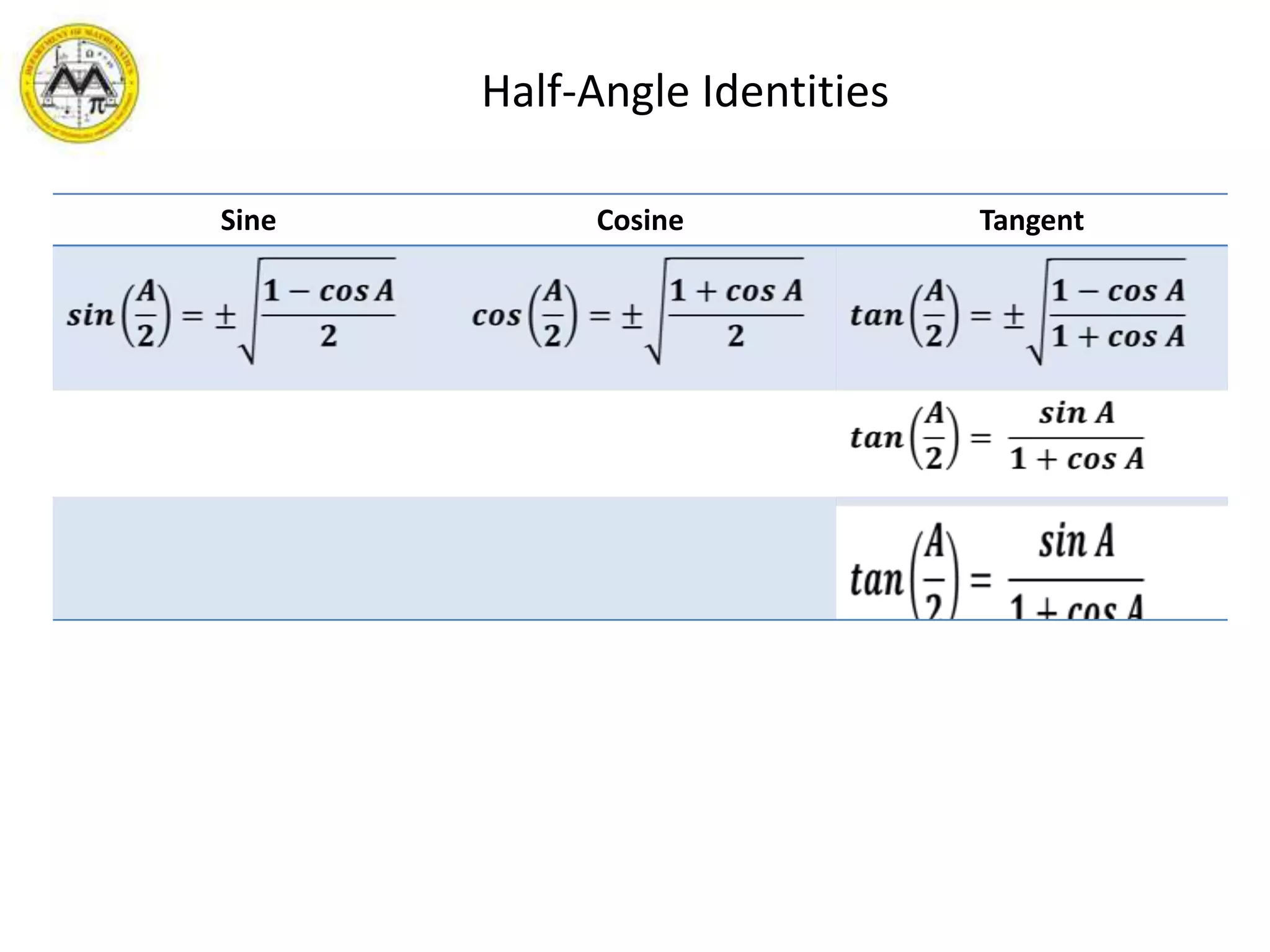
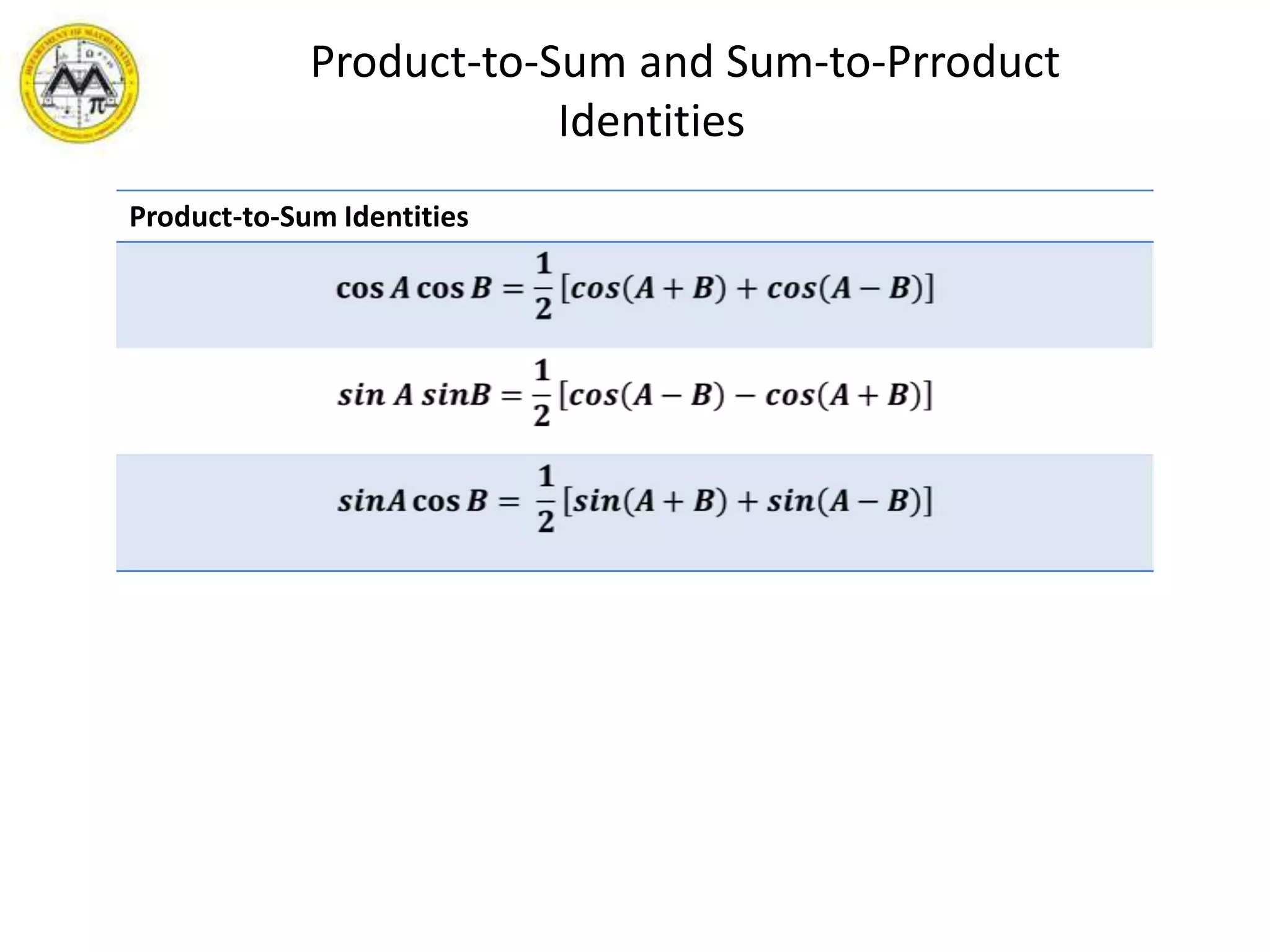
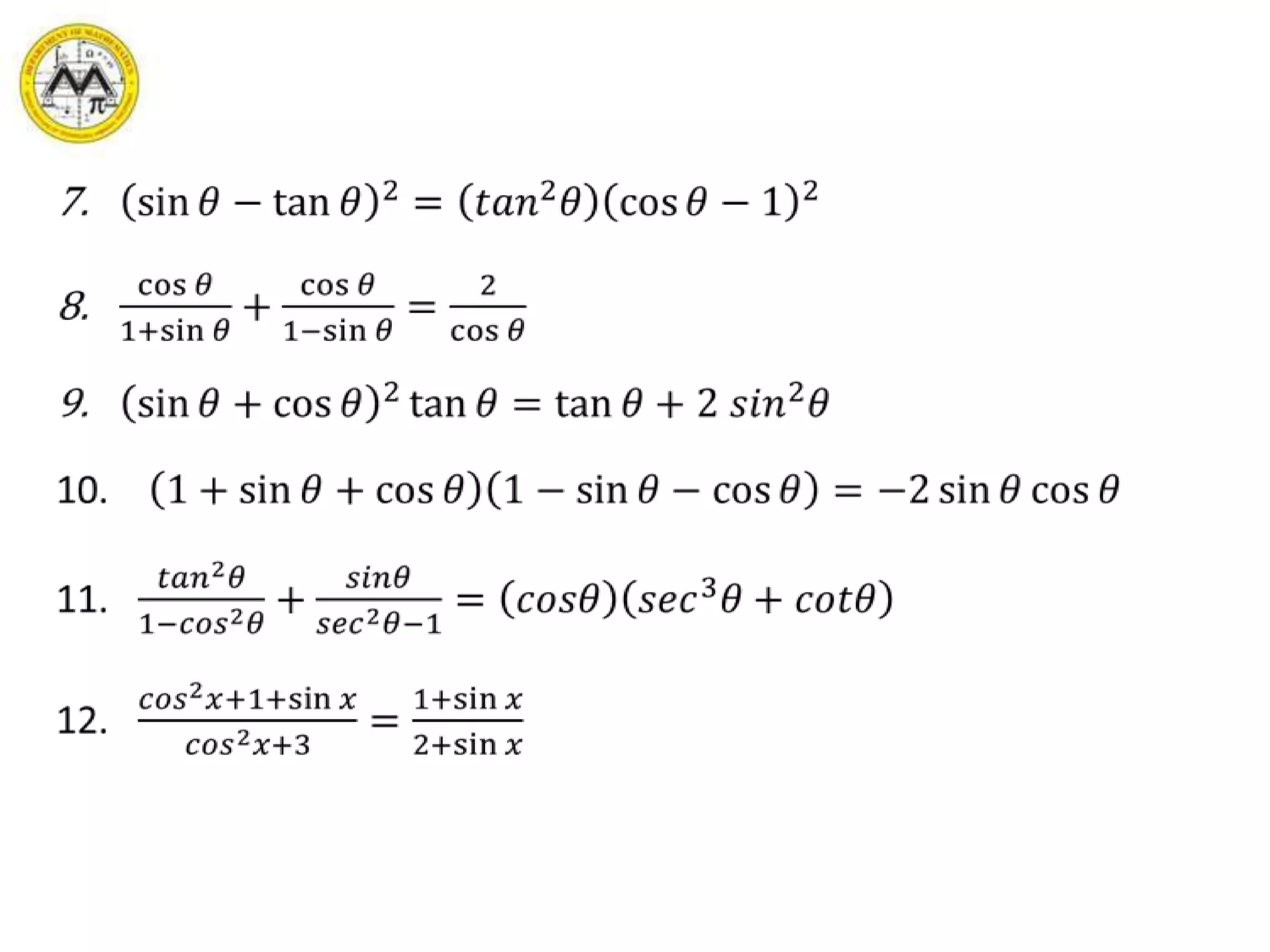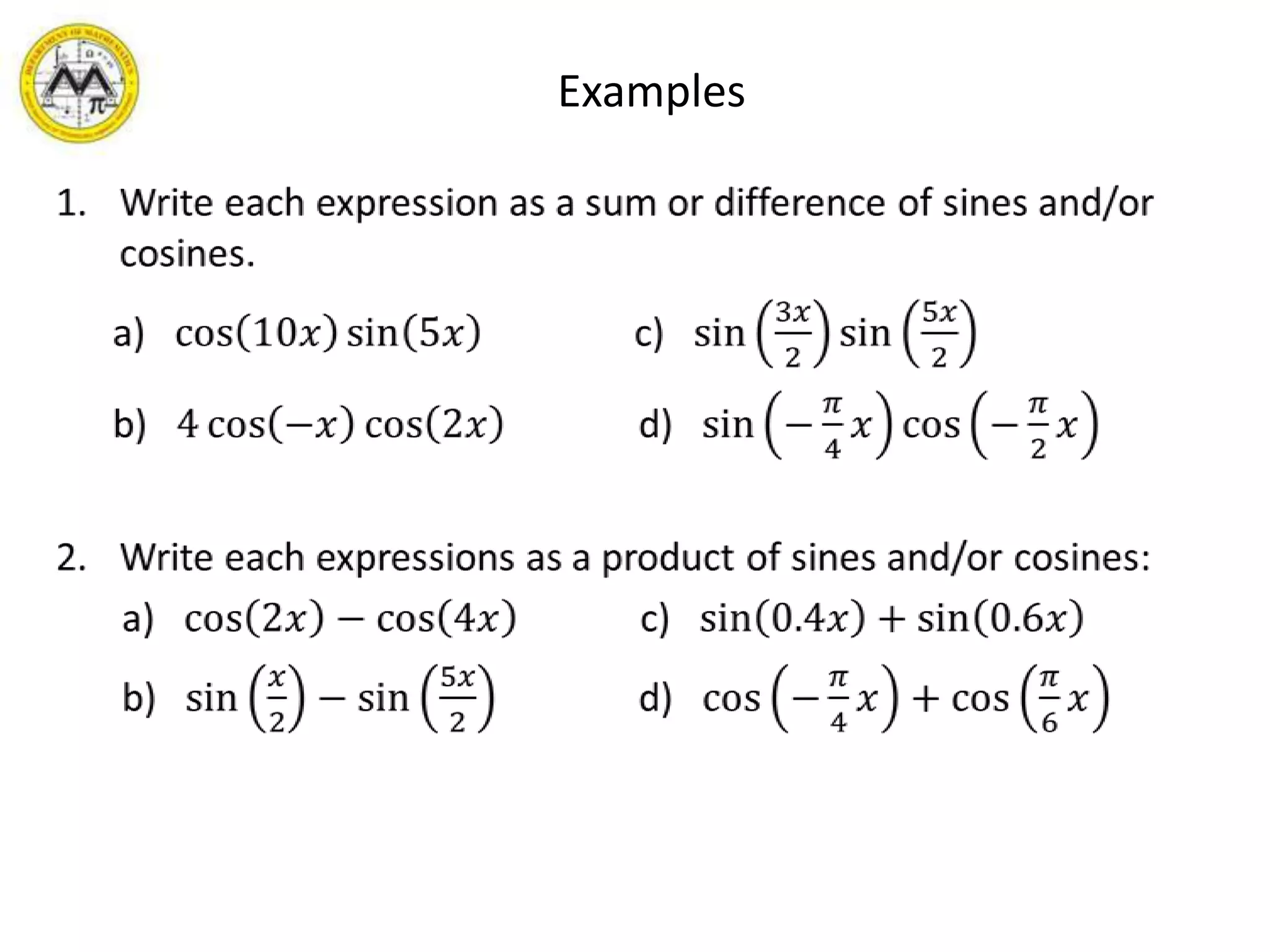This document provides an overview of trigonometric identities and examples of their applications. It discusses basic identities, verifying identities, and advanced identities involving sums, differences, doubles angles, and half angles. Examples are provided for applying product-to-sum and sum-to-product identities. The objectives are to review and apply various trigonometric identities to simplify expressions and evaluate functions.

1. Lesson 6: TRIGONOMETRIC IDENTITIESMath 12 Plane and Spherical Trigonometry

2. OBJECTIVESAt the end of the lesson the students are expected to:Review basic identities.Simplify a trigonometric expression using identities.Verify a trigonometric identity.Apply the sum and difference identities.Apply the double-angle and half-angle identities.Apply the product-to-sum and sum-to-product identities.

3. TRIGONOMETRIC IDENTITIESA trigonometric identity is an equation involving trigonometric functions that hold for all values of the argument, typically chosen to be 𝜃.

4. BASIC TRIGONOMETRIC IDENTITIESReciprocal Identities

5. Quotient (or Ratio) Identities

6. Pythagorean IdentitiesNegative Arguments Identities

7. Guidelines for Verifying Trigonometric IdentitiesThe following suggestions help guide the way to verifying trigonometric identities:Start with the more complicated side of the equation.Combine all sums and differences of fractions (quotients) into a single fraction (quotient).Use basic trigonometric identities.Use algebraic techniques to manipulate one side of the other side of the equation is achieved.Sometimes it is helpful to convert all trigonometric functions into sines and cosines. Note:Trigonometric identities must be valid for all values of the independent variable for which the expressions in the equation are defined (domain of the equation).

8. Examples Verify the following identities:2𝑠𝑒𝑐2𝜃=11−sin𝜃+11+sin𝜃1+cos𝜃cos𝜃=sec𝜃+1cos𝜃sec𝜃+tan𝜃=1−sin𝜃1tan𝜃+cot𝜃=sin𝜃 cos𝜃2𝑐𝑜𝑠2𝜃−1=𝑐𝑜𝑠4𝜃−𝑠𝑖𝑛4𝜃tan𝑥+cot𝑥=csc𝑥sec𝑥

9. sin𝜃−tan𝜃2=𝑡𝑎𝑛2𝜃cos𝜃−12cos𝜃1+sin𝜃+cos𝜃1−sin𝜃=2cos𝜃sin𝜃+cos𝜃2tan𝜃=tan𝜃+2 𝑠𝑖𝑛2𝜃1+sin𝜃+cos𝜃1−sin𝜃−cos𝜃=−2sin𝜃cos𝜃𝑡𝑎𝑛2𝜃1−𝑐𝑜𝑠2𝜃+𝑠𝑖𝑛𝜃𝑠𝑒𝑐2𝜃−1=𝑐𝑜𝑠𝜃𝑠𝑒𝑐3𝜃+𝑐𝑜𝑡𝜃𝑐𝑜𝑠2𝑥+1+sin𝑥𝑐𝑜𝑠2𝑥+3=1+sin𝑥2+sin𝑥

10. Sum and Difference Identities

11. Examples 1. Find the exact value for each trigonometric expression. a) sin𝜋12 b) sin105° c) tan165°2. Write each expression as a single trigonometric function. a) sin2𝑥sin3𝑥+cos2𝑥cos3𝑥 b) cos𝜋−𝑥sin𝑥+sin𝜋−𝑥cos𝑥 c) tan49°+tan23°1−tan49°tan23°Find the exact value of a) sin𝛼−𝛽 and b) 𝑡𝑎𝑛𝛼+𝛽 if sin𝛼=−35 and sin𝛽=15; the terminal side of 𝛼 lies in Q3 and the terminal side of 𝛽 lies in Q1.Verify: sin𝑥−𝜋2=cos𝑥+𝜋2

12. Double-Angle Identities

13. ExamplesIf cos𝑥=513 and sin𝑥<0, find a) tan2𝑥 b) cos2𝑥If csc𝑥=−25 and 𝜋<𝑥<3𝜋2, find sin2𝑥.Simplify each expression and evaluate the resulting expression exactly, if possible. a) 2tan15°1−𝑡𝑎𝑛215° b) 𝑐𝑜𝑠2𝑥+2−𝑠𝑖𝑛2𝑥+2Verify each identity. a) sin𝑥+cos𝑥2=1+sin2𝑥 b) sin3𝑥 =sin𝑥4𝑐𝑜𝑠2𝑥−1

14. Half-Angle Identities

15. ExamplesUse half-angle identities to find the exact values of the following: a) cos22.5° b) cot7𝜋8 c) sin75°2. If csc𝑥=−3 and cos𝑥>0, find cos𝑥2.If cot𝑥=−245 and 𝜋2<𝑥<𝜋, find sin𝑥2.Verify the following: a) sin−𝑥=−2sin𝑥2cos𝑥2.

16. Product-to-Sum and Sum-to-Prroduct Identities

17. Product-to-Sum and Sum-to-Product Identities

18. ExamplesWrite each expression as a sum or difference of sines and/or cosines. a) cos10𝑥sin5𝑥 c) sin3𝑥2sin5𝑥2 b) 4cos−𝑥cos2𝑥 d) sin−𝜋4𝑥cos−𝜋2𝑥Write each expressions as a product of sines and/or cosines: a) cos2𝑥−cos4𝑥 c) sin0.4𝑥+sin0.6𝑥 b) sin𝑥2−sin5𝑥2 d) cos−𝜋4𝑥+cos𝜋6𝑥

19. ExamplesSimplify the following trigonometric expressions: a) cos3𝑥−cos𝑥sin3𝑥+sin𝑥 b) cos5𝑥+cos2𝑥sin5𝑥−sin2𝑥Verify the following: a) 𝑠𝑖𝑛 𝐴+sin𝐵cos𝐴+cos𝐵=𝑡𝑎𝑛𝐴+𝐵2 b) sin𝐴−sin𝐵𝑐𝑜𝑠𝐴+𝑐𝑜𝑠𝐵=𝑡𝑎𝑛𝐴−𝐵2

20. ReferencesAlgebra and Trigonometry by Cynthia YoungTrigonometry by Jerome Hayden and Bettye HallTrigonometry by Academe/Scott, ForesmanPlane and Spherical Trigonometry by Paul Rider