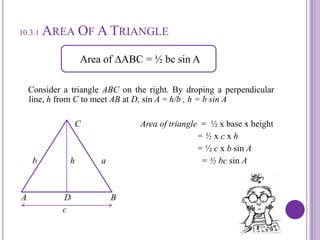
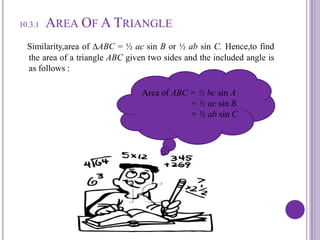
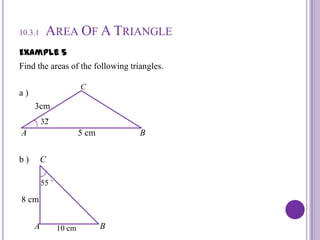
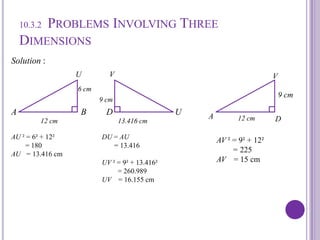
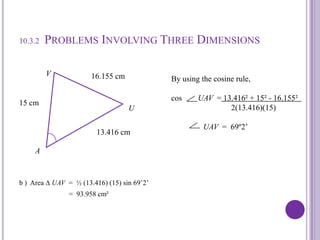
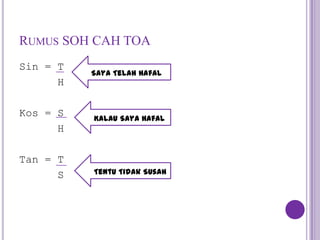
This document discusses calculating the area of triangles. It explains that the area of a triangle is 1/2 * base * height. It provides formulas to calculate the area using two sides and the included angle. Examples are given to demonstrate calculating areas when given side lengths and angles. The document also discusses a problem involving finding the area of a triangle within a three-dimensional pyramid structure. Formulas for trigonometric functions are reviewed.

1. 10.3 The Area Of A TrianglePrepared By,AsnitaMapasisiNurulHanisahHalbaniSharmizaAdlinaJunaidi

2. 10.3.1 Area Of A Triangle Consider a triangle ABC on the right. By dropinga perpendicular line, h from C to meet AB at D, sin A = h/b , h = b sin A CArea of triangle = ½ x base x height = ½ x c x h = ½ c x b sin A b h a = ½ bcsin A A D B c Area of ∆ABC = ½ bc sin A

3. 10.3.1 Area Of A TriangleSimilarity,area of ∆ABC = ½ ac sin B or ½ absin C. Hence,to find the area of a triangle ABC given two sides and the included angle is as follows :Area of ABC = ½ bcsin A = ½ ac sin B = ½ absin C

4. 10.3.1 Area Of A TriangleExample 5Find the areas of the following triangles.a ) 3cm A 5 cm Bb ) C8 cm A BC32̊ 55 ˚10 cm

5. 10.3.1Area Of A TriangleSolution :a ) Area of ∆ ABC = ½ bcsin A = ½ (3)(5) sin 32= 3.97 cm²b ) By using the sine rule b = c b = 40˚ 57’ sin b sin c = 180˚ - 55˚- 40˚57’8 = 10 = 84˚3’sin bsin 55˚ sin b = 8 ( sin 55˚ ) ABC = ½ bcsin A 10 = ½ (8)(10) sin 84˚3’ = 39.78 cm²

6. 10.3.2Problems Involving Three DimensionsExample 6 The diagram on the right shows a pyramid of height 9 cm and stands on a square base of 12 cm.The vertex V is vertically above the point D and U is the midpoint of BC.Calculate,A ) UAV B ) the area of ∆UAV 9 cmVDCUA12 cm12 cmB

7. 10.3.2 Problems Involving Three DimensionsSolution :U VA B D UV6 cm9 cm9 cmAD12 cm12 cm13.416 cmAU ² = 6² + 12² = 180AU = 13.416 cmDU = AU = 13.416UV ² = 9² + 13.416² = 260.989UV = 16.155 cmAV ² = 9² + 12² = 225AV = 15 cm

8. 10.3.2 Problems Involving Three Dimensionsb ) Area ∆ UAV = ½ (13.416) (15) sin 69˚2’ = 93.958 cm²V16.155 cmBy using the cosine rule,cosUAV = 13.416² + 15² - 16.155² 2(13.416)(15)UAV = 69º2’15 cmU13.416 cmA

9. Rumus SOH CAH TOASin = T HKos = S HTan = T SSayaTelahHafalKalauSayaHafalTentuTidak Susah

10. Prepared By,NurulHanisahHalbaniAsnitaMapasisiSharmizaAdlinaJunaidi