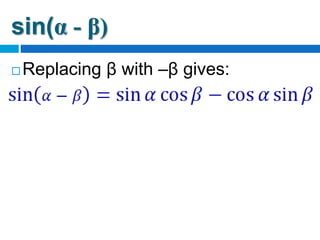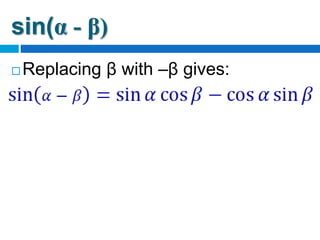
1. The document derives sum and difference formulas for sine and cosine using the law of cosines, distance formula, and cofunction relationships. 2. These formulas allow rewriting angles as sums or differences of special angles from the unit circle, which can be used to find exact values of trigonometric functions. 3. Examples are provided to demonstrate applying the formulas to find exact trigonometric values or prove trigonometric identities. Practice problems are also included.

1. 10-1 Sum and Difference
Formulas for Sine and
Cosine
Objectives:
1. Derive and apply sum and
difference formulas for sine and
cosine.

2. Investigation
 Evaluate each expression:
 cos (45° - 30°) =
 cos 45° - cos 30° =
 sin (60° - 45°) =
 sin 60° - sin 45° =
 What do you notice?

3. Deriving cos(α - β)
 By law of cosines:

4.  By the distance formula:
 Therefore:

5. cos(α + β)
 Remember:
 cos (-β) = cos β
 sin (- β) = - sin β
 So:

6. Deriving sin(α + β)
 Using the cofunction relationship
 Then:

7. sin(α - β)
 Replacing β with –β gives:

8. Formula Recap

9. Rewriting
 Rewrite each angle as a sum or
difference using special angles from
the unit circle:
 285°
 75°
 -15°
 -165°

10. Example 1:
 Find the exact value of sin 15°.

11. Example 2:
 Find the exact value of:

12. You Try!
 Find the exact value of each:
 cos 15°


13. Example 3:
 Show that

14. Example 4:
 Prove that

15. You Try!
 Prove that

16. Example 5:
 Suppose that and

17. You Try!
 Suppose that and