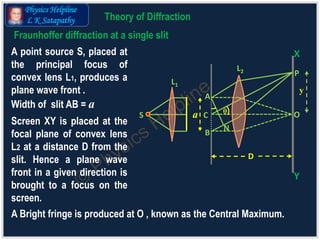
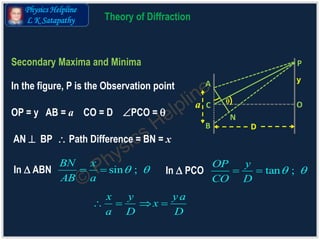
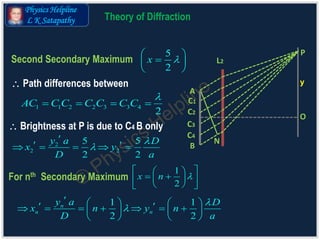
The document explains the theory of diffraction, detailing how light bends around obstacles and the phenomena of bright and dark fringes produced in diffraction patterns. It discusses two main types of diffraction: Fresnel (with finite distances) and Fraunhofer (with infinite distances), including the formation of plane wave fronts. Additionally, it covers concepts such as secondary maxima and minima, calculations for path differences, and the width of fringes.

1. Physics Helpline
L K Satapathy Theory of Diffraction
Diffraction
Maxima and Minima
Fringe Width
Central Maximum

2. Physics Helpline
L K Satapathy
Diffraction is the phenomenon of bending of light around sharp
corners and spreading into regions of geometrical shadow. This takes
place at narrow slits and apertures, whose size is comparable to the
wavelength of light used.
Fresnel Diffraction : In this type of diffraction, the source of light and
the screen are at finite distance from the slit.
Fraunhoffer Diffraction : In this type of diffraction, the source of light
and the screen are at infinite distance from the slit. Hence , a plane
wave front is incident on the slit and the diffracted wave front is also
plane.
Theory of Diffraction

3. Physics Helpline
L K Satapathy
CONCEPTS
A wave front is the locus of the particles of the medium
which are in the same phase of vibration
S
A
B
C
 For a point source of light S , the rays are radial
For points A , B and C , SA = SB = SC
 Particles at A , B and C are vibrating in phase
 ABC is a spherical wave front with source S as the centre.
 Rays of light are perpendicular to the wave front
For a light source at infinity, the rays are parallel
 A Plane wave front is produced
Theory of Diffraction

4. Physics Helpline
L K Satapathy Theory of Diffraction
To obtain a plane wave front with source of light at a finite distance
S
A
B
A'
B'f
 A point source S is placed at the principal focus
of a convex lens.  The refracted rays are parallel.
A plane wave front is produced from a point source at
finite distance by using a convex lens, which is equivalent to
placing the source at infinity.
AB is the spherical wave front incident on the lens
A'B' is the plane wave front produced by the lens

5. Physics Helpline
L K Satapathy Theory of Diffraction
A point source S, placed at
the principal focus of
convex lens L1, produces a
plane wave front .
Width of slit AB = a 
a
D
S
A
B
C
N
O
P
y
L1
L2
X
Y
Screen XY is placed at the
focal plane of convex lens
L2 at a distance D from the
slit. Hence a plane wave
front in a given direction is
brought to a focus on the
screen.
A Bright fringe is produced at O , known as the Central Maximum.
Fraunhoffer diffraction at a single slit

6. Physics Helpline
L K Satapathy Theory of Diffraction
Secondary Maxima and Minima
sin
BN x
AB a
   ;

a
D
A
B
C
N
O
P
y
In the figure, P is the Observation point
OP = y AB = a CO = D PCO = 
AN  BP  Path Difference = BN = x
In  ABN tan
OP y
CO D
   ;In  PCO
x y ya
x
a D D
   

7. Physics Helpline
L K Satapathy Theory of Diffraction
A
B
C
N
P
y
M
O
L2
Secondary minima: when path difference x is an even multiple of /2
First Secondary Minimum
2
BN CM

  
1 1( )We x x and ypu yt   
1
1 1
y a D
x y
D a

    

8. Physics Helpline
L K Satapathy Theory of Diffraction
Second Secondary Minimum  2x 
1 1 2 2 3 3
2
AC C C C C C B

   
2 2( 2 )x x and y y   
2
2 22 2
y a D
x y
D a

    
 Path differences between
In general , for nth Secondary Minimum  x n
n
n n
y a D
x n y n
D a

    
A
B N
O
P
y
C1
C2
L2
C3

9. Physics Helpline
L K Satapathy Theory of Diffraction
Secondary maxima: when path difference x is an odd multiple of /2
First Secondary Maximum
3
2
x 
 
 
 
1 1 2 (
2
)destroyeC C C dA

 
1 1x x and y y  
1
1 1
3 3
2 2
y a D
x y
D a



     
A
B N
O
P
y
C1
C2
L2
 Path differences between
 Brightness at P is due to C2 B only

10. Physics Helpline
L K Satapathy Theory of Diffraction
Second Secondary Maximum
5
2
x 
 
 
 
1 1 2 2 3 3 4
2
AC C C C C C C

   
2
2 2
5 5
2 2
y a D
x y
D a



     
 Path differences between
 Brightness at P is due to C4 B only
For nth Secondary Maximum
1
2
x n 
  
   
  
1 1
2 2
n
n n
y a D
x n y n
D a


              
   
A
B
N
O
P
y
C1
C2
L2
C3
C4

11. Physics Helpline
L K Satapathy Theory of Diffraction
Width of Secondary Bright Fringe = Distance between positions of two
successive dark fringes.
1 ( 1)n n
D D D
y y n n
a a a
  
       
Width of Secondary Dark Fringe = Distance between positions of two
successive bright fringes.
1
1
( )
1
2 2
n n
D D D
y y n n
a a a


 
 
   
            
 

 
Width of Central Bright Fringe = Distance between positions of two first
secondary dark fringes on either side of the centre of screen.
( 2 2 )2o
D D D
a a a
 


 
 
     
 
 

12. Physics Helpline
L K Satapathy
For More details:
www.physics-helpline.com
Subscribe our channel:
youtube.com/physics-helpline
Follow us on Facebook and Twitter:
facebook.com/physics-helpline
twitter.com/physics-helpline