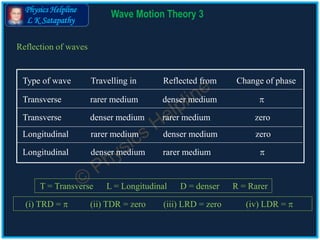
The document discusses wave motion theory, focusing on the reflection of waves and stationary waves. It explains the formation of stationary waves through the interference of two identical waves traveling in opposite directions, detailing nodes and antinodes along a stretched string. Additionally, it outlines laws governing the frequencies and vibrations of strings, including the relationship between frequency, tension, length, and mass per unit length.

1. Physics Helpline
L K Satapathy
Wave Motion Theory 3
Reflection of waves
Travelling and Stationary waves
Nodes and Anti-nodes
Stationary waves in strings
Laws of vibrations of strings

2. Physics Helpline
L K Satapathy
Wave Motion Theory 3
Reflection of waves
Type of wave Travelling in Reflected from Change of phase
Transverse rarer medium denser medium 
Transverse denser medium rarer medium zero
Longitudinal rarer medium denser medium zero
Longitudinal denser medium rarer medium 
(i) TRD =  (ii) TDR = zero (iii) LRD = zero (iv) LDR = 
T = Transverse L = Longitudinal D = denser R = Rarer

3. Physics Helpline
L K Satapathy
Wave Motion Theory 3
Stationary waves : When two identical waves travelling along the same straight
line in opposite directions interfere , stationary waves are formed.
Consider two waves of the same amplitude , frequency and wavelength
travelling in opposite directions along a stretched string , given by
1
2
sin( )
sin( )
y A Kx t
and y A Kx t


 
 
1 2 sin( ) sin( )y y y A Kx t A Kx t      
2 sin cosy A Kx t 
This is the Eqn of a stationary wave of amplitude 2AsinKx
 Resultant displacement
 Amplitude of different particles are different

4. Physics Helpline
L K Satapathy
Wave Motion Theory 3
Antinodes : These are points of maximum amplitude (=2A)
 For antinodes , we have sin 1 (2 1) [ 0,1,2 . . . ]
2
Kx Kx n n

     
2
(2 1) (2 1)
2 4
x n x n
  

     
 Antinodes are obtained at
3 5
, , . . .
4 4 44
oddx
    
 
 

Nodes : These are points of zero amplitude
 For nodes , we have sin 0
2
n
Kx Kx n x

    
 Nodes are obtained at
2 3
0 , , , . . .
2 2 2
x
  

Distance between two successive nodes (or antinodes) =  / 2
As particle at the nodes are always at rest, energy is not transmitted across them

5. Physics Helpline
L K Satapathy
Wave Motion Theory 3
Stationary Wave
Amplitudes of all particles are same
Travelling Wave
Particles at nodes are permanently at restNo particle is permanently at rest
Amplitudes of diff. particles are diff.
All the particles reach mean position
simultaneously
All particles do not reach mean position
simultaneously
Phase of all particles between two successive
nodes are same
Phase of particles in one wavelength are
different
Energy is not transmitted along the waveEnergy is transmitted along the wave
Different particles pass through their mean
positions with different speeds
All particles pass through their mean
positions with the same speed

6. Physics Helpline
L K Satapathy
Wave Motion Theory 3
Stationary waves in stretched strings :
Consider a string stretched between two fixed points. When it is set into vibration,
a transverse wave travels along the string, which is reflected from the other end.
The incident and the reflected waves superpose to produce stationary waves in the
string. Since the two ends of the string are fixed, these are always nodes.
Fundamental frequency ( First harmonic ) :
L
A B
In this mode of vibration, the string vibrates in
one segment with one antinode between the two
nodes at the ends A and B .
Let wavelength = , frequency = and speed of wave1 1f
T
v


1
1 2
2
AB L L

    
1
1
1
2 2
v v T
f
L L 
   

7. Physics Helpline
L K Satapathy
Wave Motion Theory 3
First overtone ( Second harmonic ) :
In this mode of vibration, the string vibrates in
two segments with one node between the two
nodes at the ends A and B .
Let wavelength = , frequency =2 2f 2AB L   
2 1
2
2 2
2
v v v
f f
L L
 
     
 
L
A B
 In general , frequency of the harmonic or overtone isth
n ( 1)th
n 
1
2 2
n
v n T
f n n f
L L 
 
   
 
 For a string fixed at both ends , the frequencies obtained are
[ All members of the harmonic series ]
1 1 1, 2 , 3 . . .f f f
Speed v = constant
 f is doubled
when  is halved

8. Physics Helpline
L K Satapathy
Wave Motion Theory 3
Laws of transverse vibrations of stretched strings :
Fundamental frequency of a stretched string is given by
1
2
T
f
L 

Law of length :
1
f
L

Law of Tension : f T
Law of Mass/unit length :
1
f


Law of Diameter and density : Let diameter of cross-section = D , density = 
Mass / unit length
2
4
D
area density

    2
1 1 1
f f f
DD 
     
Law of Diameter : [ L ,  , T are constants ]
1
f
D

Law of density : [ L , D , T are constants ]
1
f



9. Physics Helpline
L K Satapathy
For More details:
www.physics-helpline.com
Subscribe our channel:
youtube.com/physics-helpline
Follow us on Facebook and Twitter:
facebook.com/physics-helpline
twitter.com/physics-helpline