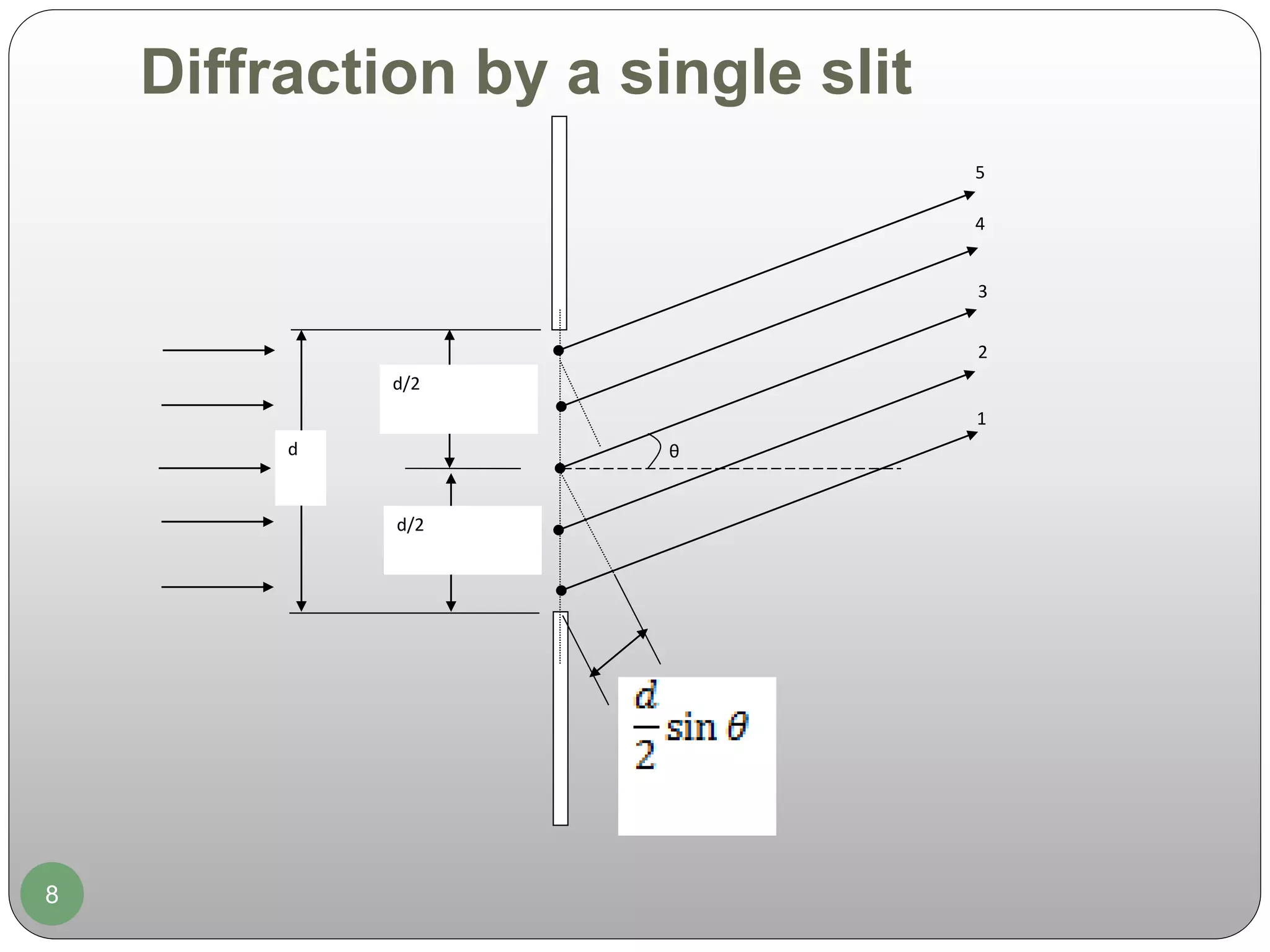
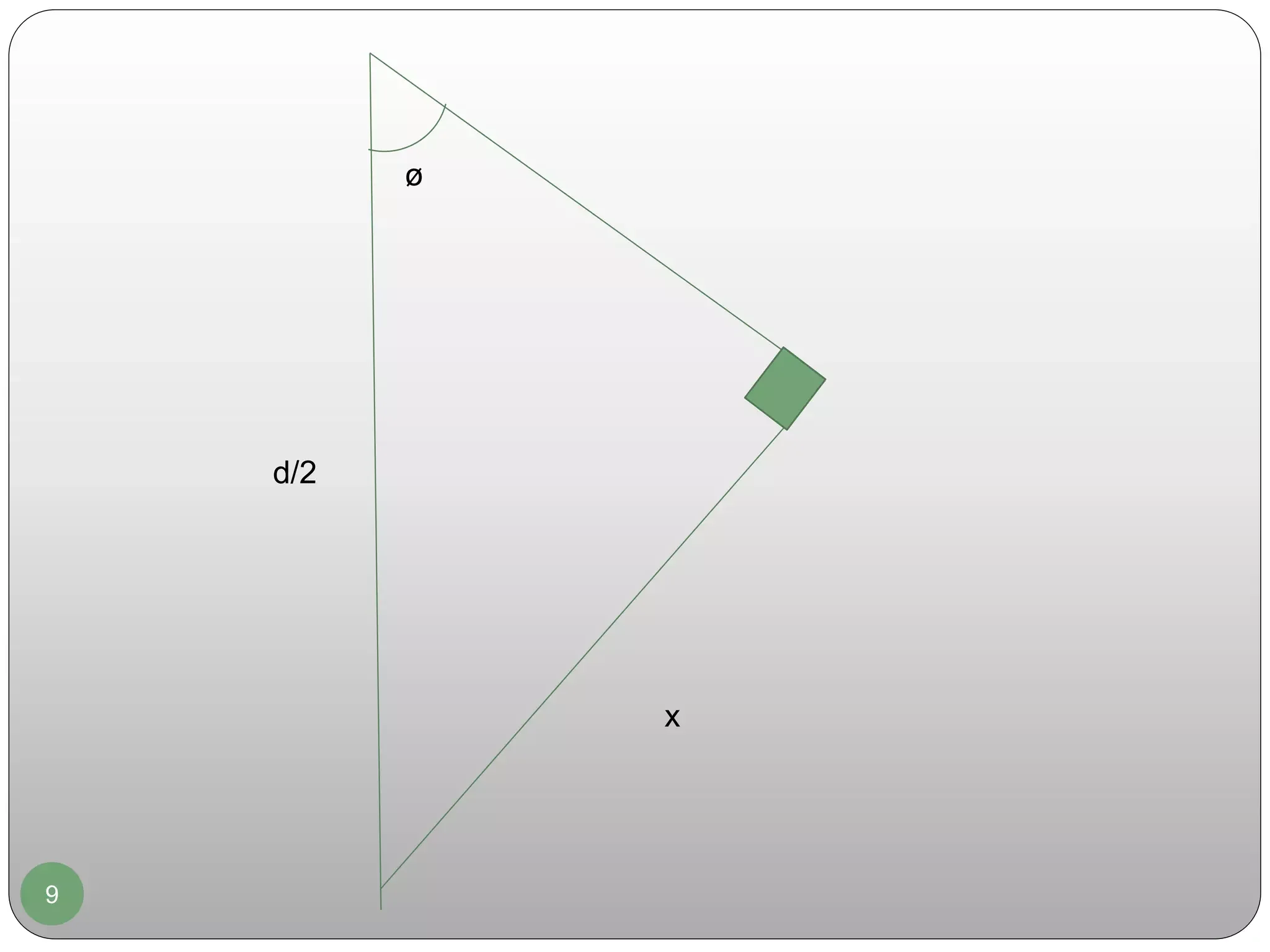
This document discusses the topic of diffraction, which is the spreading or bending of waves as they pass through an aperture or around obstacles. It defines diffraction and provides examples of how it occurs with light, sound waves, and radio signals. The key types of diffraction are Fresnel diffraction, which occurs when the source and screen are not far apart, and Fraunhofer diffraction, which occurs when they are farther apart. The document also examines diffraction patterns produced by single slits and circular apertures, providing equations to calculate dark fringe locations and the radius of the first dark ring.

1. ROBERT ESHUN
S.L.T Department
Accra Polytechnic
Chapter 6
Diffraction

2. 2
 Diffraction
 The spreading or bending of waves as they pass
through an aperture or round the edge of a barrier.
 The change in direction of waves that occurs when
they pass the edge of an obstacle or through a
narrow opening.
 Diffraction of light takes place only if the size of
an obstacle is comparable to the wavelength of
light.

3. 3

4. 4

5. 5
 Examples
 CD or DVDs: closely spaced tracks act as
diffraction grating to form rainbow pattern seen
when looking at a disk.
 Sound waves: Sound can bend around corners.
Sound can be heard even though a listener may not
be in line of sight of the source.
 TV and radio reception (such as mobile phones):
Diffraction around large hills reduces so people
below the hill are unable to receive the signal.
Telcos set up more transmitters for their customers
to receive the service.

6. 6
 In Fraunhoffer diffraction:
 The source and the screen are far away from each
other.
 Incident wave fronts on the diffracting obstacle are
plane.
 Diffracting obstacle give rise to wave fronts which
are also plane.
 Plane diffracting wave fronts are converged by
means of a convex lens to produce diffraction
pattern.

7. 7
 In Fresnel diffraction:
 Source and screen are not far away from each
other.
 Incident wave fronts are spherical.
 Wave fronts leaving the obstacles are also
spherical.
 Convex lens is not needed to converge the
spherical wave fronts.

8. Diffraction by a single slit
8
d
d/2
d/2
θ
1
2
3
4
5

9. 9
d/2
x
ø

10. 10
Therefore the path difference x is:

11. 11
 If this path difference is half of a wavelength,
destructive interference occurs, the waves
annihilate each other and a dark fringe is obtained.

12. 12
 Dividing the slit in 4, a dark fringe is obtained when
 Dividing the slit in 6, a dark fringe is obtained when
 Dividing the slit in 8, a dark fringe is obtained when
 Generally, a dark fringe is obtained when
where

13. Diffraction by a circular aperture
(Circular hole)
13
 Airy’s disc - circular disc surrounded by much
fainter concentric circular rings
 First dark ring is formed an angle θ, such that
 d - diameter of aperture,
 d << l, l being the perpendicular distance from the
screen to the hole

14. 14
 Radius of first dark ring
 If diffracted light is converged with a convex lens
onto screen placed at its focal length, f, radius of
the first dark ring is