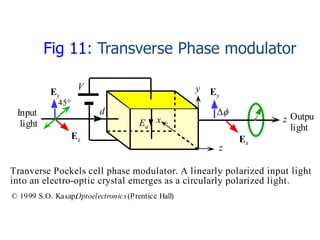
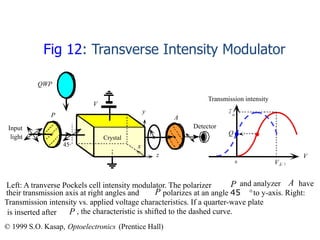
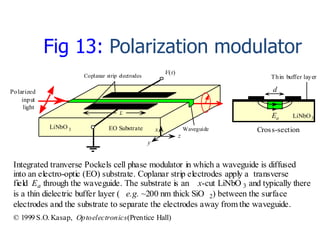
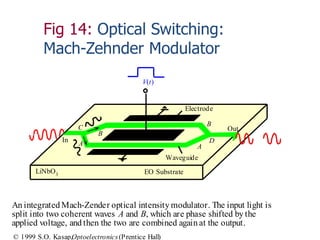
This document defines electro-optic effects and describes how an external electric field can induce changes in the refractive index of a material, modulating its optical properties. It discusses the Pockels effect specifically, where a linear change in refractive index occurs due to an applied electric field. This effect can be used to build integrated optical modulators and switches, such as a transverse Pockels cell that inserts a phase difference between orthogonal field components, acting as a polarization modulator. The phase difference can be converted to an intensity variation using an interferometer such as a Mach-Zehnder configuration.

1. Electro-Optic Effects: definition
• Electro-optic effects refer to changes in the refractive
index of a material induced by the application of an
external electric field
– Which therefore modulates the optical properties
– The applied field is not the electric field of any light wave but a
separate external field
• We can apply an external field by placing electrodes on
opposite faces of a crystal and connecting these
electrodes to a battery
– The presence of the field distorts the electron motions in the
atoms/molecules of the substance
– Distorts the crystal structure resulting in changes in optical
properties

2. Electro-optic effect
• An applied external field can cause an optically
isotropic crystal such as GaAs to become birefringent
– The field induces principal axes and an optic axis
– Typically changes in the refractive index are small
– The frequency of the applied field has to be such that the
field appears static over the time scale it takes for the
medium to change its properties, as well as for any light to
cross the substance
• The electro-optic effect are classified according to first
or second order effects

3. Field induced refractive index
• Take the refractive index n to be a function of the applied E-field,
that is n=n(E), we can expand this as a Taylor series in E. The new
refractive index n’would be:
n’= n + a1E + a2E 2+.…
– where the coefficients are called the linear electro-optic effect and second
order electro-optic effect coefficients.
• The change in n due to the first E term is called the Pockels effect
n = a1E
• The change in n due to the second E 2 term is called the Kerr
effect and a2=K where K is called the Kerr coefficient
n = a2 E 2 = (K) E 2

4. Pockels Effect
• Suppose x, y and z are principal axes of a crystal with
refractive indices n1, n2 and n3 along these directions
– For an optically isotropic crystal, these would be the same
– For a uniaxial crystal n1= n2  n3
• Apply a voltage across a crystal and thereby apply an
external dc field Ea along z-axis
– In Pockels effect, the field will modify the optical indicatrix.
– The exact effect depends on the crystal structure
– GaAs (isotropic) with a spherical indicatrix becomes birefringent
– KDP (potassium dihydrogen phosphate) that is uniaxial becomes
biaxial

5. Pockels Effect: KDP (KH2PO4)
• The field Ea along z rotates the principal axes by 45
about z
• Changes the principal indices as shown in Fig.10(b)
– The new principal indices are now n1’ & n2’, which means the
cross section is now an ellipse
– Propagation along the z-axis under an applied field now
occurs with different refractive indices n1’ & n2’
– The applied field induces new principal axes x’ & y’ for this
crystal

6. x
z Ea
n1 = no
y
(a)
x
n2 = no
n1
n2
z
(b)
x
45
(c)
xz
KDP, LiNbO 3 KDP LiNbO 3
n1
n2
y Ea
y
(a) Cross section of the optical indicatrix with no applied field, n1 = n2 = no (b) The
applied external field modifies the optical indicatrix. In a KDP crystal, it rotates the
principal axes by 45  to x and y and n1 and n2 change to n1 and n2 . (c) Applied
field along y in LiNbO 2 modifies the indicatrix and changes n1 and n2 change to n1
and n2 .
© 1999 S.O. Kasap,Optoelectronics(Prentice Hall)
Fig 10: Pockels Effect

7. Pockels Effect: LiNbO3
• In the case lithium niobate (uniaxial crystal), a field Ea is
applied along the y-direction
– It does not significantly rotate the principal axes
– changes the principal refractive indices n1 & n2 (both equal to
no) to n1’ & n2’ as shown in Fig 10(c)
• Consider a wave propagating along the z-direction
(optic axis) in the crystal
– Before a field Ea is applied, this wave experience n1=n2=no
whatever in the polarization as Fig 10(a)
– In the presence of an applied field Ea, the light propagates as
two orthogonally polarized waves (parallel to x and y)
experiencing different refractive indices n1’ & n2’

8. Pockels Effect: LiNbO3, cont
• The applied field thus induces a birefringence for light
traveling along the z-axis.
• The field induced rotation of principal axes is
neglected.
• The Pockels effect gives the new refractive indices n1’
& n2’ in the presence of Ea as
n1 ’  n1 + ½ n1
3 r22 Ea & n2 ’  n2 – ½ n2
3 r22 Ea
where r22 is a constant, called a Pockels coeffient that depends
on the crystal structure and the material.

9. Phase modulator
• It is clear that the control of the refractive index by
an external applied field is a distinct advantage that
enables the phase change through a Pockels crystal
to be controlled or modulated
– Such a phase modulator is called a Pockels cell
• In the longitudinal Pockels cell phase modulator, the
applied field is in the direction of light propagation ->
Fig 10(b)
• In the transverse phase modulator, the applied field
is transverse to the direction of light propagation ->
Fig 10(c)

11. Transverse Phase Modulator
• The applied field Ea = V/d is applied parallel to the y-direction (normal to the
direction of light propagation along z)
• The incident beam is linearly polarized at 45 to the y-axis.
– It is represented in terms of polarizations (Ex & Ey components) along the x and y
axes
– Ex & Ey experience refractive indices nx & ny.
• When Ex traverses the length distance L, its phase changes by 1.
• When Ey traverses the distance L, its phase changes by 2, given by a similar
expression except that r22 changes sign. Thus, the phase changes between two
components is









d
V
rnn
L
L
n
oo 22
3
2
11
1
22





V
d
L
rno 22
3
21
2


 

12. Polarization modulator
• The applied voltage thus inserts an adjustable phase
different  between the two field components
– The polarization state of the output wave can be controlled
by the applied voltage and the Pockels cell is a polarization
modulator.
• The medium can be changed from a quarter-wave to a
half-wave plate by simply adjusting V.
– The voltage V = V/2 , the half-wave voltage and generate a
half-wave plate ( )

13. Output
light

z
x
Ex
d
Ey
V
z
Ex
Ey
y

Input
light Ea
Tranverse Pockels cell phase modulator. A linearly polarized input light
into an electro-optic crystal emerges as a circularly polarized light.
© 1999 S.O. Kasap,Optoelectronics(Prentice Hall)
Fig 11: Transverse Phase modulator

14. Transverse Intensity Modulator
• From the polarization modulator in Fig.11, an intensity
modulator can be built as shown in Fig.12
– by inserting a polarizer P and an analyzer A before and after the phase
modulator
– P and A have their transmission axes at 90 to each other
• The transmission axis of P is at 45 to the y-axis
– The light entering the crystal has equal Ex and Ey components
• In the absence of applied voltage, two components travel with
the same refractive index and polarization output is the same as
its input
– There is no light detected at the detector as A and P are at the right angle

15. Fig 12: Transverse Intensity Modulator
Left: A tranverse Pockels cell intensity modulator. The polarizer P and analyzer A have
their transmission axis at right angles and P polarizes at an angle 45 °to y-axis. Right:
Transmission intensity vs. applied voltage characteristics. If a quarter-wave plate
is inserted after P , the characteristic is shifted to the dashed curve.
© 1999 S.O. Kasap, Optoelectronics (Prentice Hall)
Transmission intensity
V
Io
Q
0 V/ 2
V
°
Input
light
P A
Detector
Crystal
z
x
y
QWP

16. Transverse Intensity Modulator, 2
• An applied voltage inserts a phase difference  between the
two E-field components
– The light leaving the crystal now has an elliptical polarization and hence
a field components along the transmission axis of A
– A portion of this light will therefore pass through A to the detector
– The transmitted intensity now depends on the applied voltage V.
• Suppose that Eo is the amplitude of the wave incident on the
crystal face
– The amplitude along x- and y-axis will be Eo/2 each.
– Ex is along the –x direction
• The total field E at the analyzer is
     t
E
yt
E
x oo
cos
2
ˆcos
2
ˆE

17. Transverse Intensity Modulator, 3
• A factor cos(45) of each component passes through A.
– We can resolve Ex and Ey along A’s transmission axis
– Then add these components and use trigonometric identity to obtain
the field emerging from A
– The final result is
E = Eo sin( ½ ) sin(t + ½ )
• The intensity I of the detected beam is
I = Io sin2( ½ ) or
I = Io sin2(/2  V/V/2 )
where Io is the light intensity under full transmission
and V/2 is an applied voltage needed to allow full transmission

18. Example: Pockel Cell Modulator
• What should be the aspect ratio d/L for the
transverse LiNiO3 phase modulator in Fig.11 that
will operate at a free-space wavelength of 1.3mm
and will provide a phase shift  of  (half
wavelength) between the two field components
propagating through the crystal for an applied
voltage of 24V?
( no = 2.2, r22 = 3.4 10–12 m/V)

19. Solution
     
device.opticalintegratedangfabricatin
bydimplementebecanpracticein1010ratiosdevice.hethrough tpassingfrom
itpreventt willeffect thandiffractiosufferlight willthesmall,toobecomesthat when
reasonsimplefor thelikeweratioanytosetyarbitrarilcannotWe.10~bewould
ratioaspectingcorrespondtheandgreaterbet wouldcoefficienPockelsrelevantthe
axis,-ythealongelslight travtheandaxis,-zthealongappliedisfieldhein which t
tarrangemenetransverstheusetowereweIfdirection.-zthealongelinglight travand
direction-ythealongappliedfieldthehasmodulatorphaseetransversparticularThis
103.124104.32.2
103.1
2121
2
Letting
andcomponentsfieldebetween thdifferencephasefor theSubstitute
2-3-
2-
3123
62/22
3
2/22
3
2/
















d/L
d
d/L
d/L
Vrn
L
d
V
d
L
rn
VV
EE
o
o
yx













20. Integrated optical modulators

21. Phase and polarization modulation
• Integrated optics refers to the integration of various
optical devices and components on a single substrate
such as lithium niobate.
– In integrated electronics, all necessary devices are integrated
in the same semiconductor crystal substrate
• There is a distinct advantage to implementing various
optical communicated devices on the same substrate
– E.g. laser diodes, waveguides, splitters, modulators,
photodetectors etc in a miniature device

22. Polarization modulator
• Polarization modulator is shown Fig.13
– An embedded waveguide has been fabricated by implanting a
LiNbO3 substrate with Ti atoms which increase the refractive
index
– Two coplanar strip electrodes run along the waveguide and
enable the application of a transverse field Ea to light
propagation direction z
• The external modulating voltage V(t) is applied between
the coplanar to drive electrodes
– By virtue of the Pockels effect, induces a change n in the
refractive index and hence a voltage dependent phase shift
through the device

23. V(t)
Ea
Cross-section
LiNbO3
d
Thin buffer layerCoplanar strip electrodes
EO Substrate
z
y
x
Polarized
input
light
WaveguideLiNbO 3
L
Integrated tranverse Pockels cell phase modulator in which a waveguide is diffused
into an electro-optic (EO) substrate. Coplanar strip electrodes apply a transverse
field Ea through the waveguide. The substrate is an x-cut LiNbO 3 and typically there
is a thin dielectric buffer layer ( e.g. ~200 nm thick SiO 2) between the surface
electrodes and the substrate to separate the electrodes away from the waveguide.
© 1999 S.O. Kasap, Optoelectronics(Prentice Hall)
Fig 13: Polarization modulator

24. Polarization modulator, 2
• The light propagation along the guide can be represented in
terms of two orthogonal modes, Ex along x and Ey along y
– These two modes experience symmetrically opposite phase changes
– The phase shift  between the Ex and Ey polarized waves would normally
be given by Pockels effect
• In the case of the applied field is not uniform between the
electrodes and further not all applied field lines lie inside the
waveguide
– The electro-optic effect takes place over the spatial overlap region
between the applied field & the optical fields
– This spatial overlap efficiency is lumped into a coefficient G and the phase
shift  is written as
  G 2/ (no
3r22)(L/d )V
where G  0.5-0.7 for various integrated polarization modulator of this type

25. Optical Switching:
Mach-Zehnder Modulator
• One potential application of self-phase modulation is
in optical switching to switch the output from low to
high intensity in fs time scale.
• In optical switching, induced phase shift by applied
voltage can be converted to an amplitude variation
by using an interferometer
– Interferometer is a device that interferes two waves of the
same frequency but different phase

26. V(t)
LiNbO3 EO Substrate
A
B
In
OutC
D
A
B
Waveguide
Electrode
An integrated Mach-Zender optical intensity modulator. The input light is
split into two coherent waves A and B, which are phase shifted by the
applied voltage, and then the two are combined again at the output.
© 1999 S.O. Kasap,Optoelectronics(Prentice Hall)
Fig 14: Optical Switching:
Mach-Zehnder Modulator

27. Mach-Zehnder Modulator, 2
• Consider the structure shown in Fig.14, which has implanted
single mode waveguide in a LiNbO3 substrate in the geometry.
– The waveguide at the input braches out at C to two arms A and B
– These arms are later combined at D to constitute the output
– The splitting at C and combining at D involve a simple Y-junction
waveguides
• In the ideal case, the power is equally split at C so that the field
is scaled by a factor 2 going into each arm
– The structure acts as an interferometer because the two waves traveling
through the arm A and B interfere at the output port D
– The output amplitude depends on the phase difference (optical path
difference) between A and B branches

28. Mach-Zehnder Modulator, 3
• Two back-to-back identical phase modulators enable
the phase changes in A and B to be modulated.
– The applied field in branch A is in opposite direction to that
in branch B
– The refractive index changes are opposite and phase
changes in arm A and B are also opposite
• If applied voltage induces a phase change of /2 in
arm A, this will be –/2 in arm B so that A & B would
be out of phase by .
– These two waves will interfere destructively and cancel each
other at D.
– The output intensity would be zero

29. Mach-Zehnder Modulator, 4
• Since the applied voltage controls the phase difference
between the two interfering waves A and B at the
output
– This voltage also control the output light intensity (the
relationship is not linear)
• The relative phase difference between the two waves A
and B is doubled with respect to a phase change  in a
single arm
– The switching intensity can be predicted by adding waves A
and B at D with A as amplitude of wave A & B:
Eoutput  A cos(t+) + A cos(t–) = 2A cos cost

30. Mach-Zehnder Modulator, 5
• The output power is proportional to E2
output which is maximum
when  = 0. Thus,
• The derivation represents approximately the right relationship
between the power transfer and the induced phase change
per modulating arm.
• The power transfer is zero when   /2.
• In practice, the Y-junction losses and uneven splitting results
in less than ideal performance
– A and B do not totally cancel out when   /2
 
 

 2
cos
0out
out
P
P