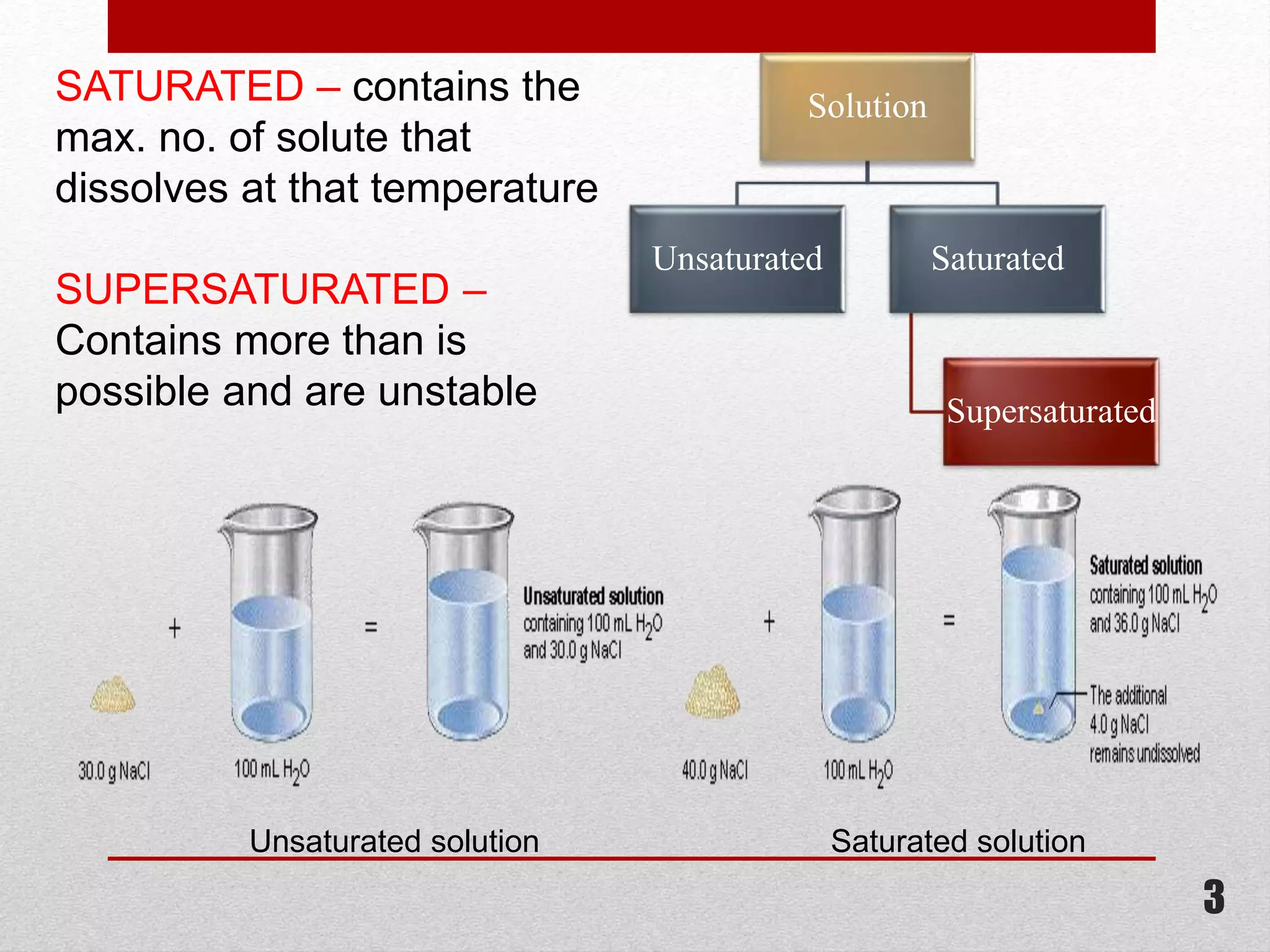
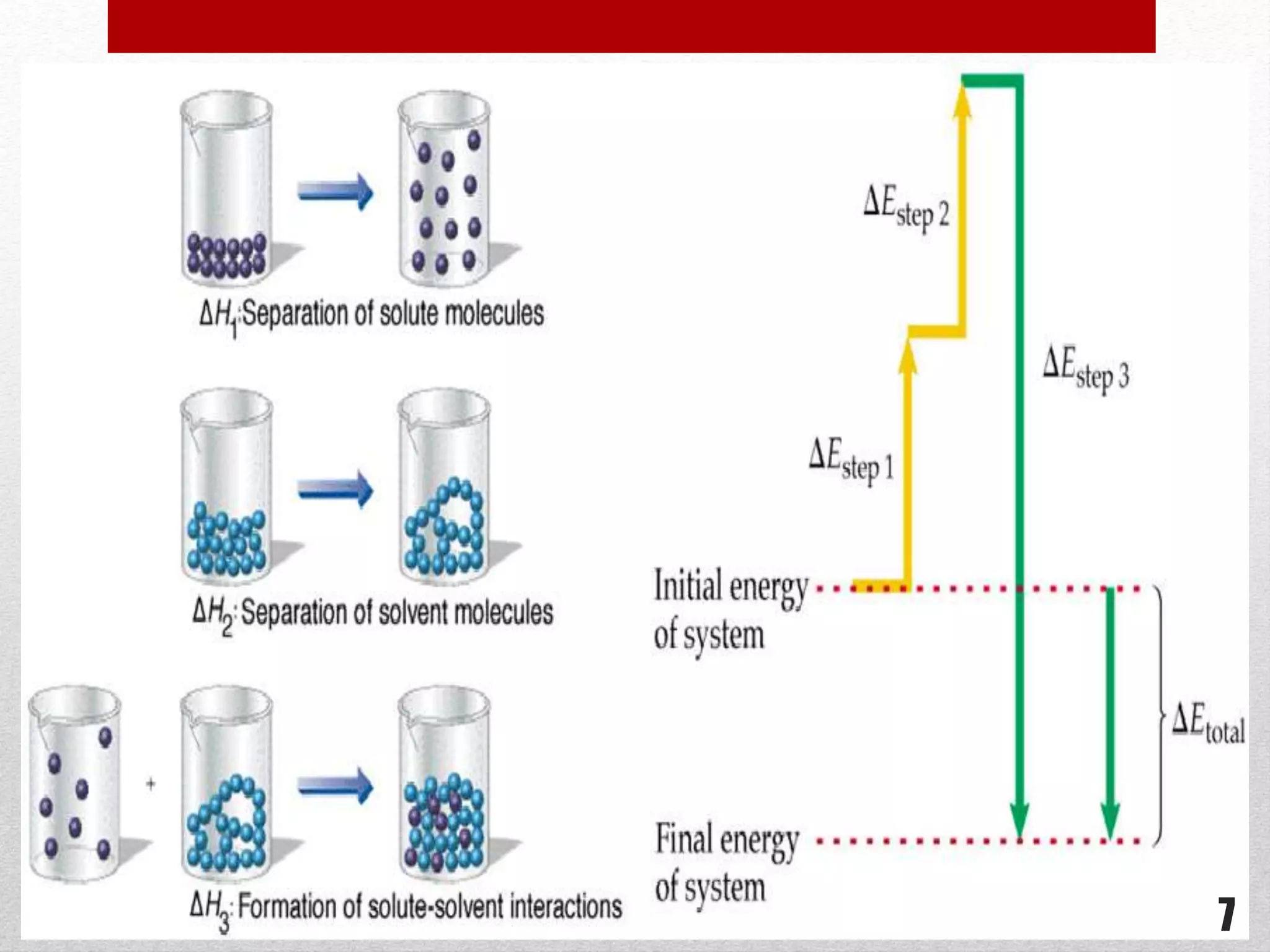
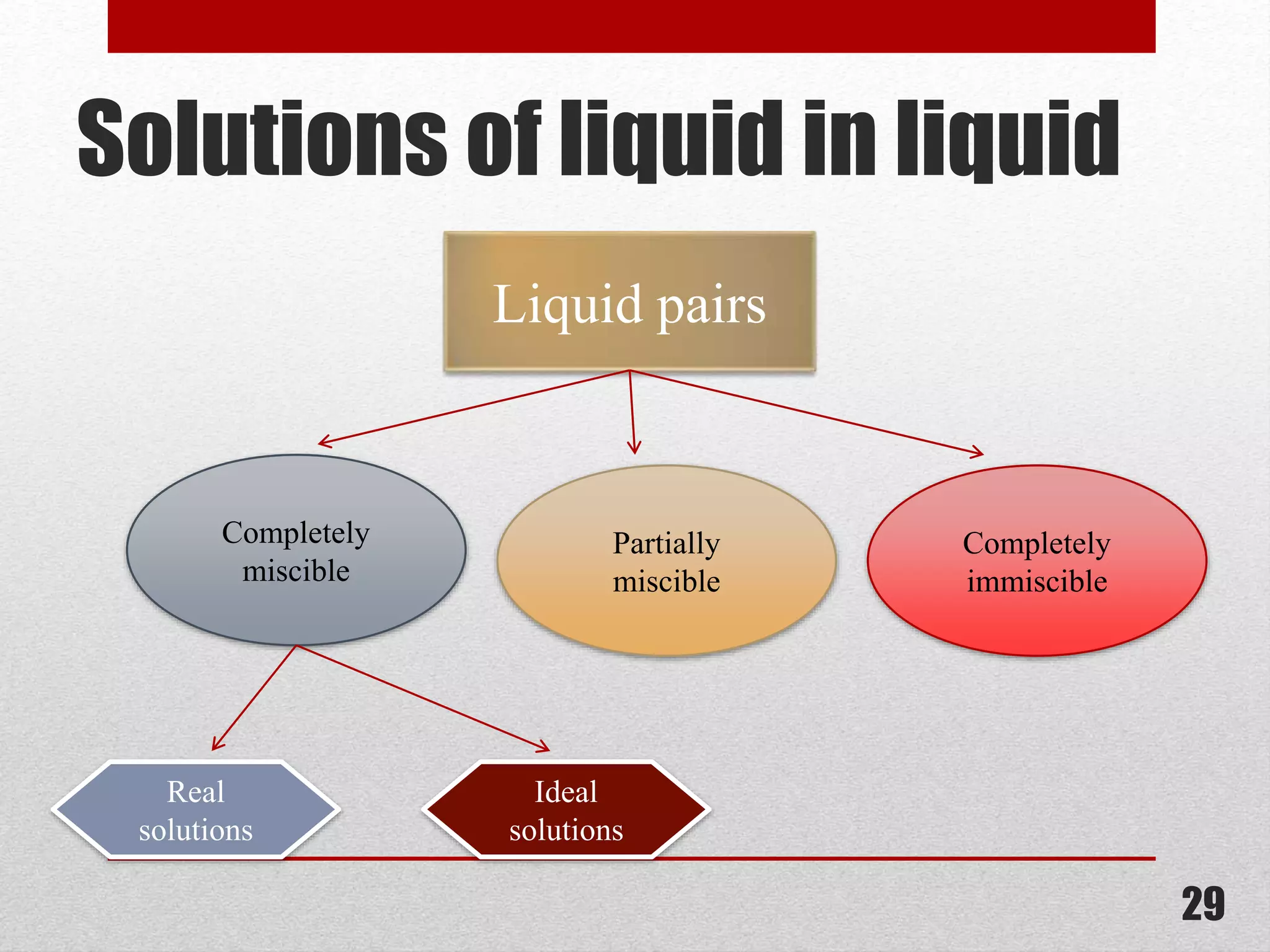
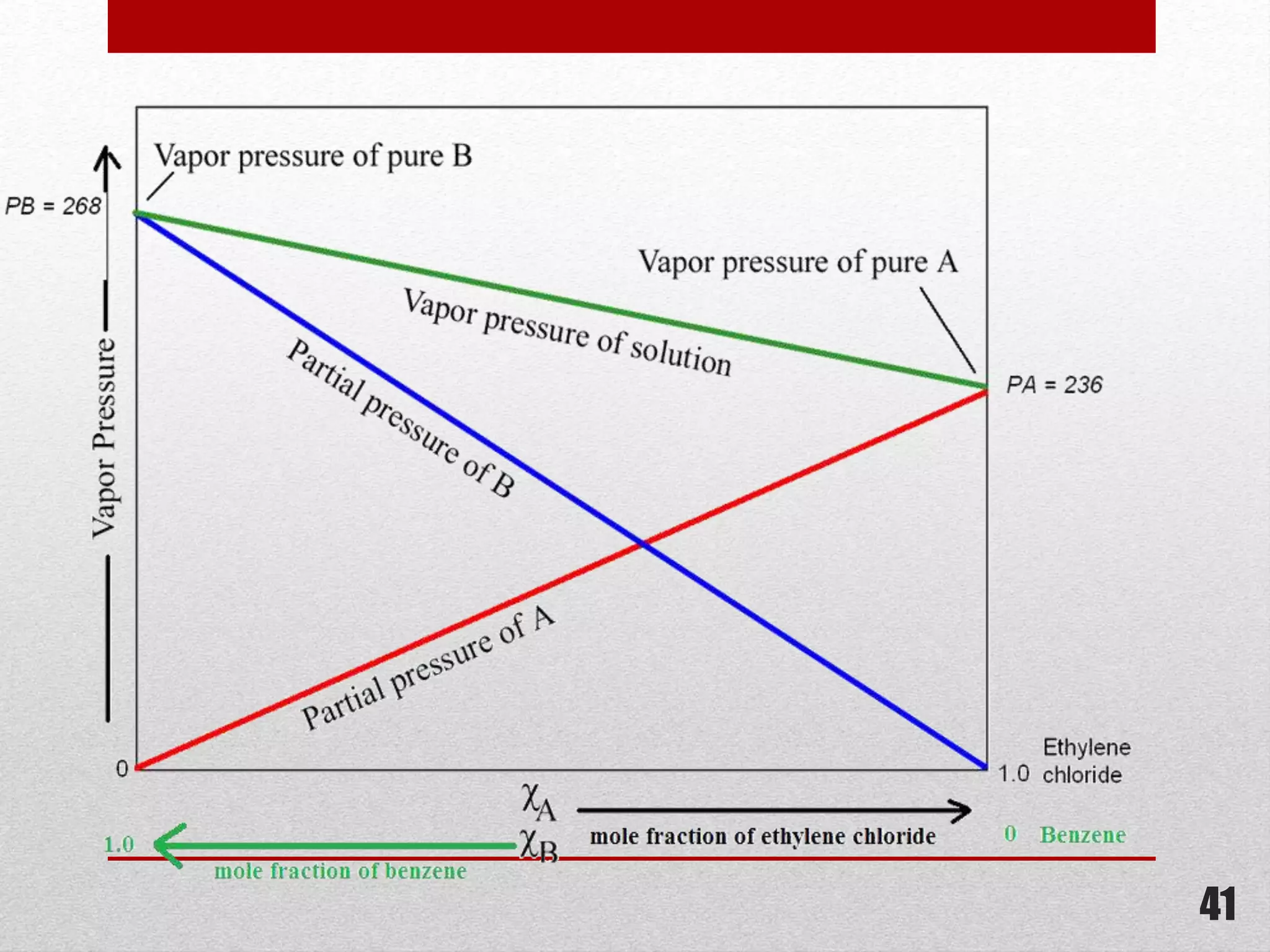
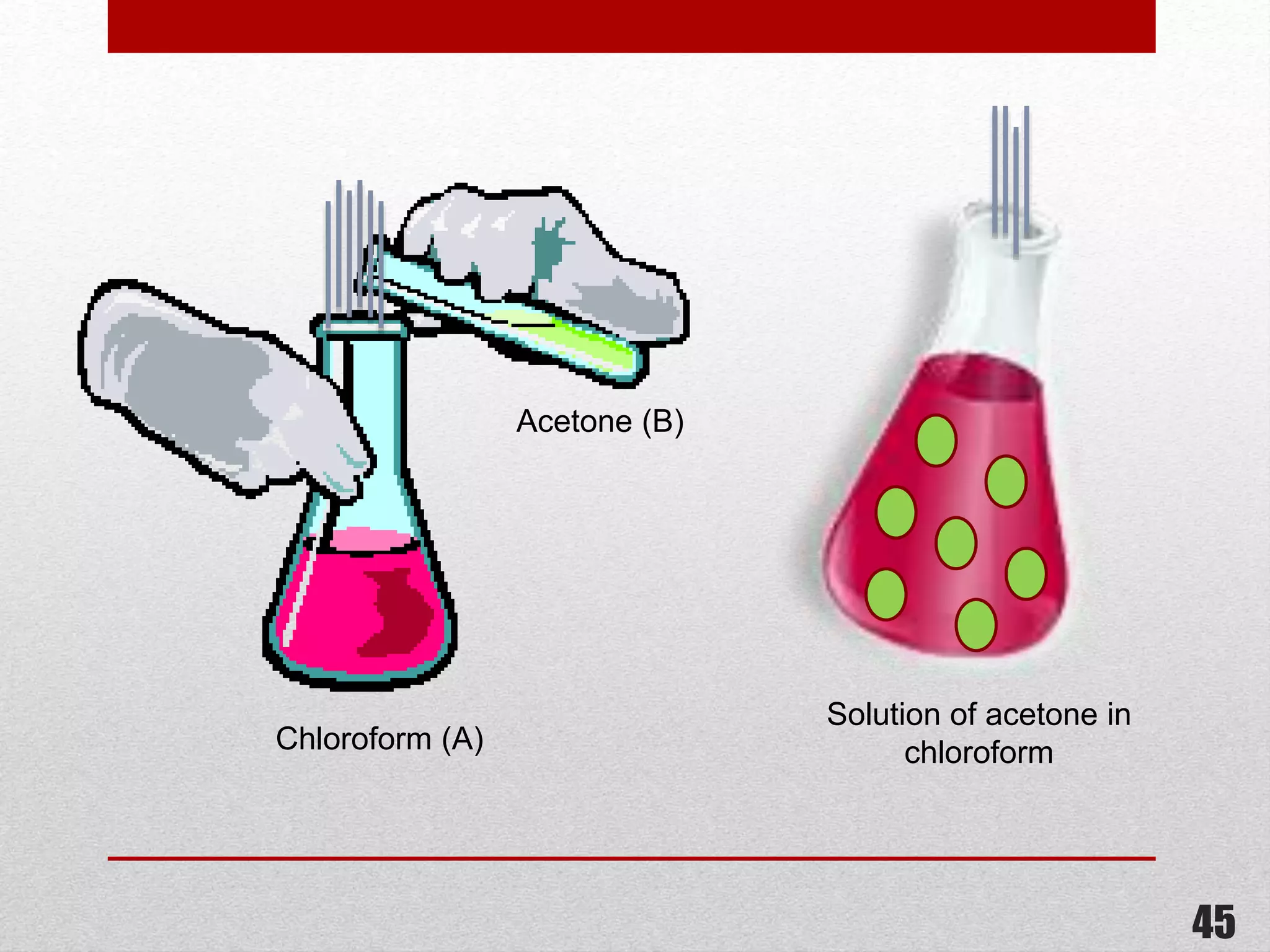
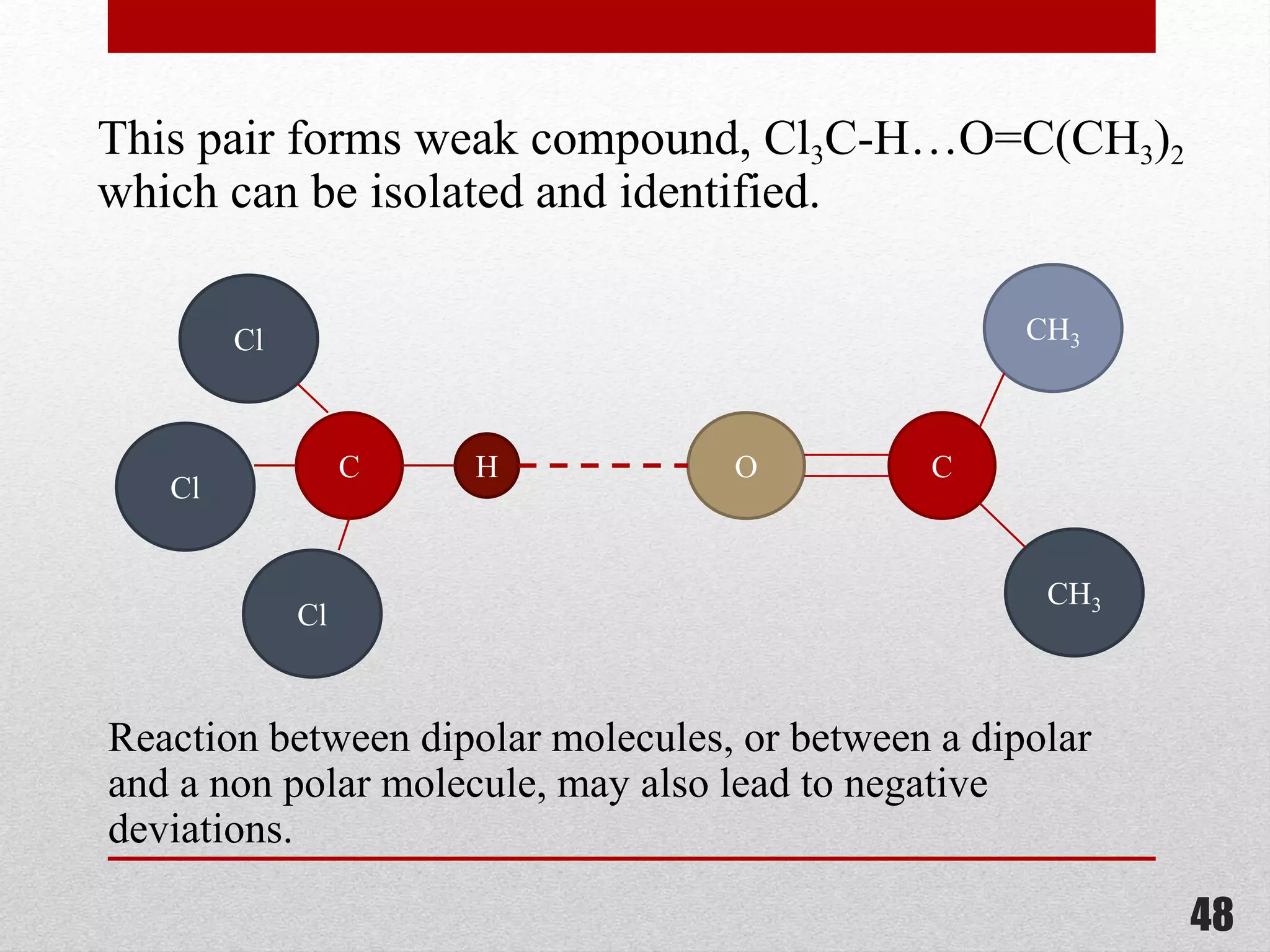
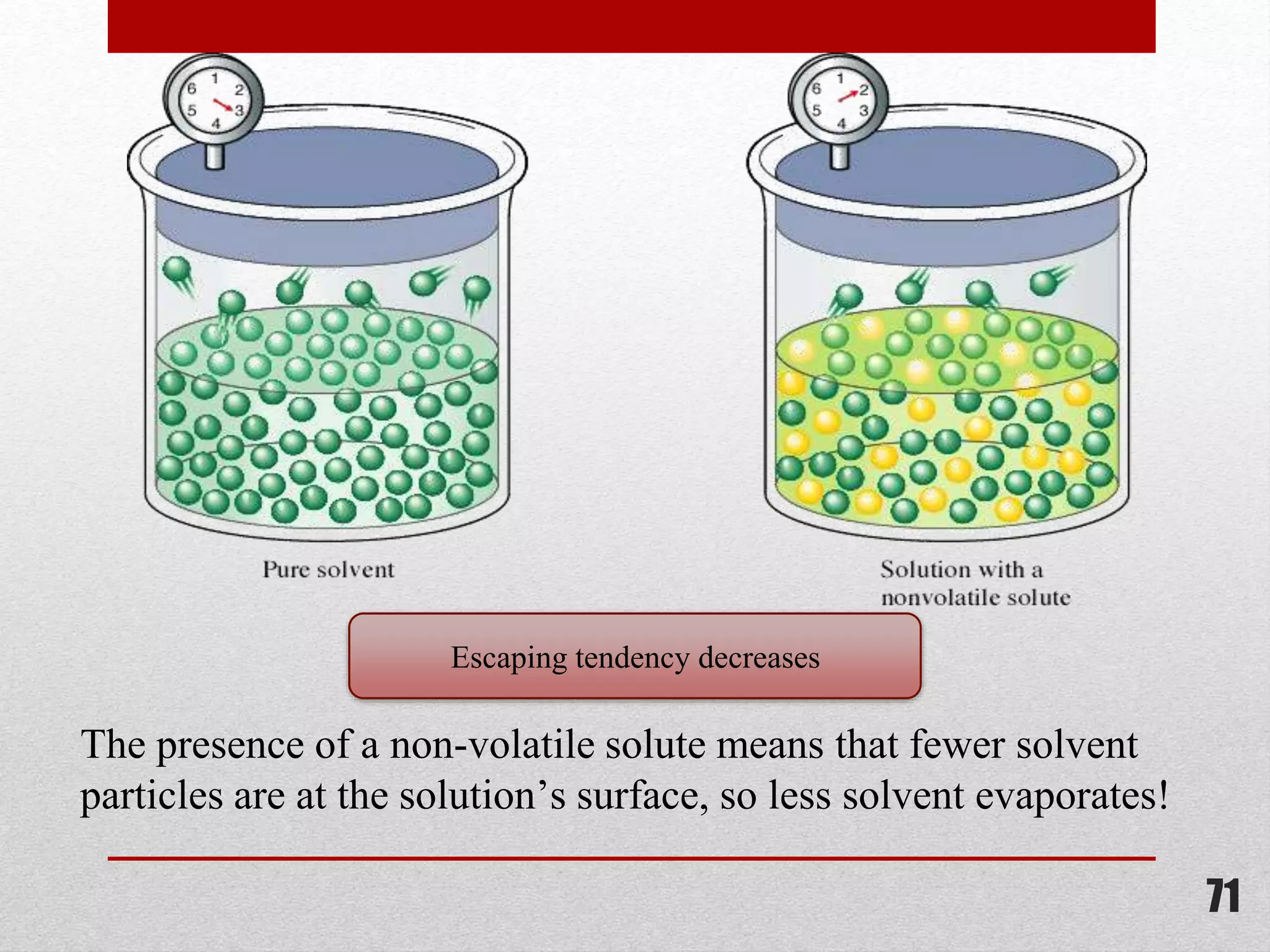
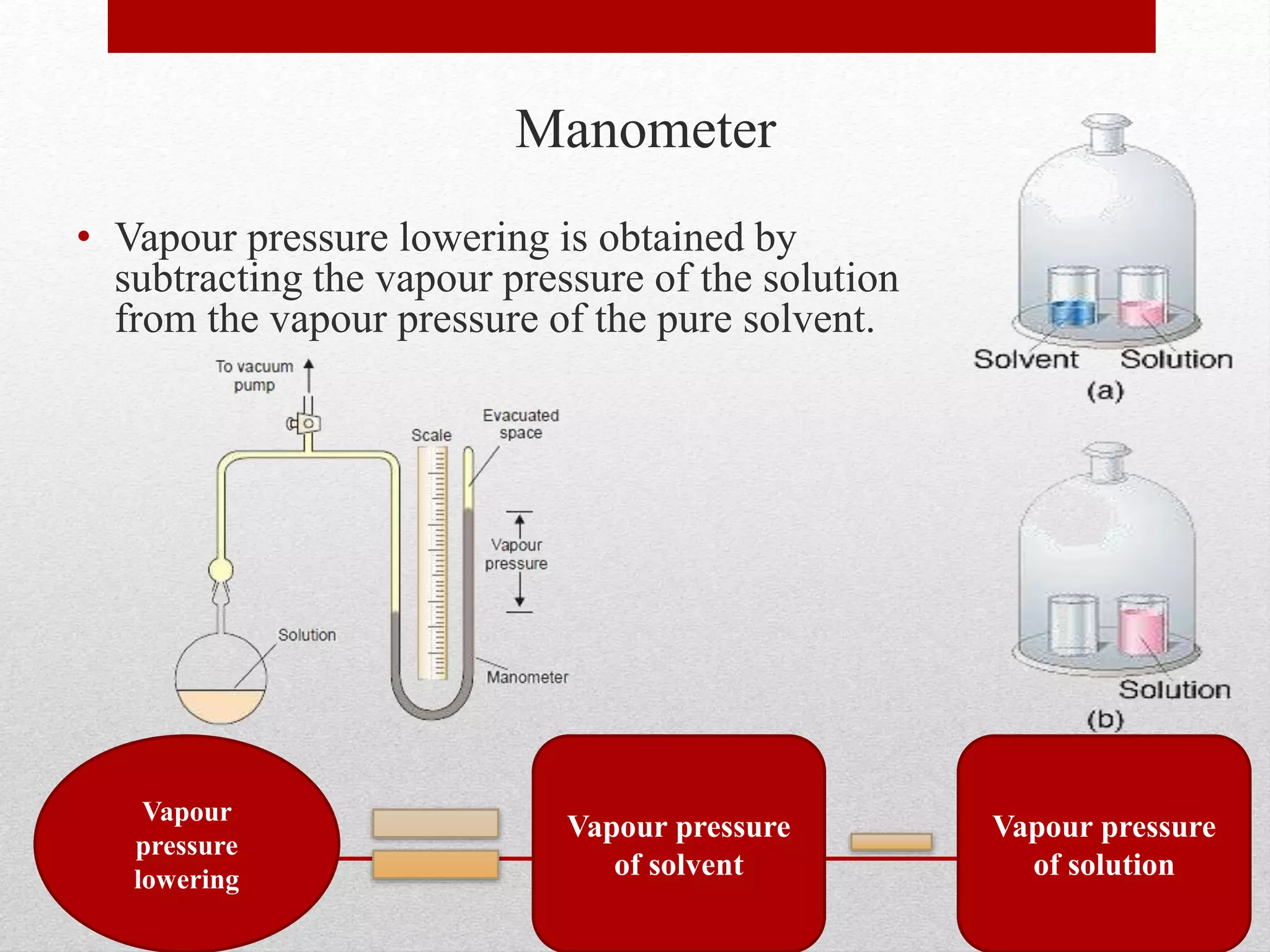
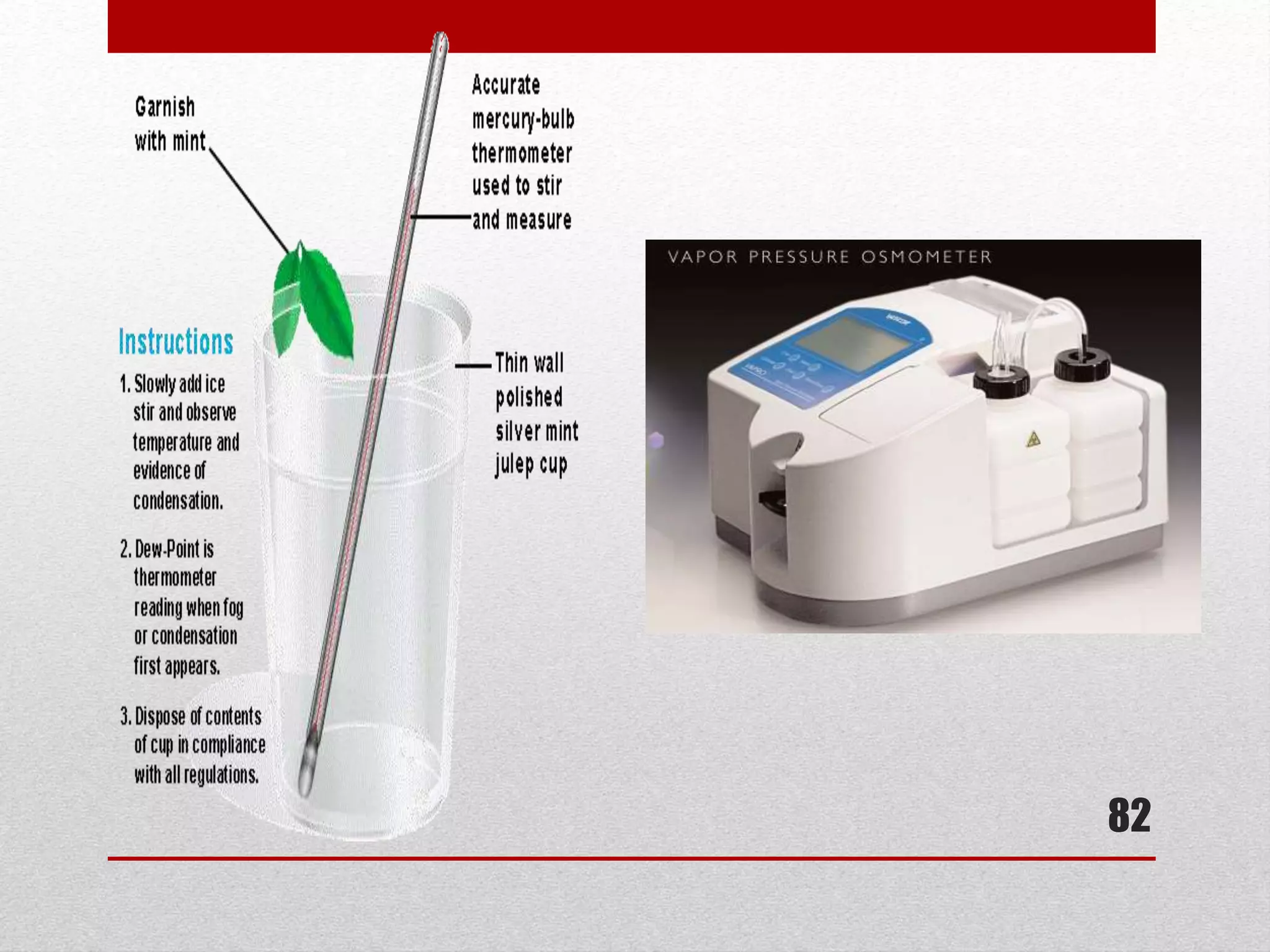
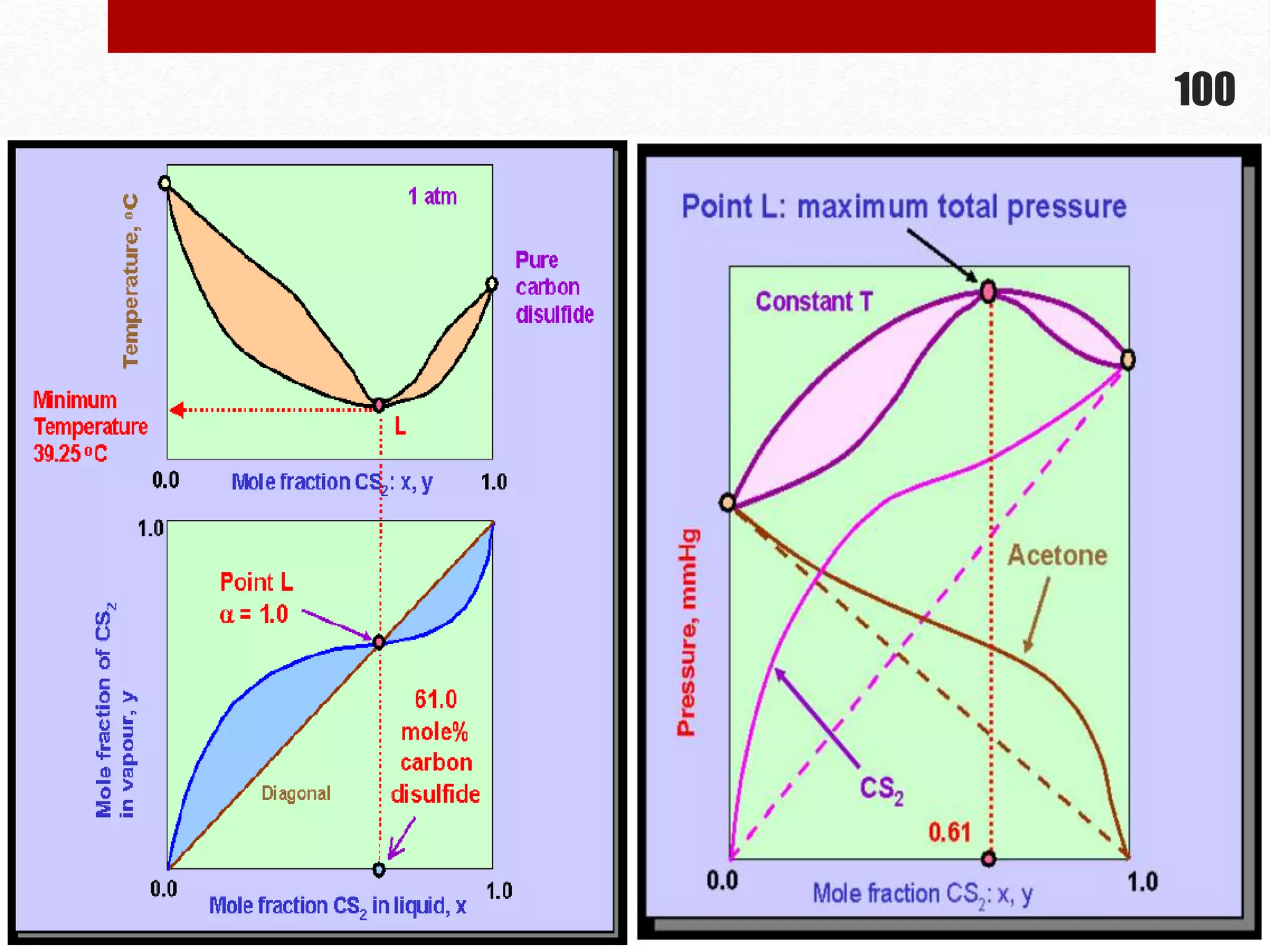
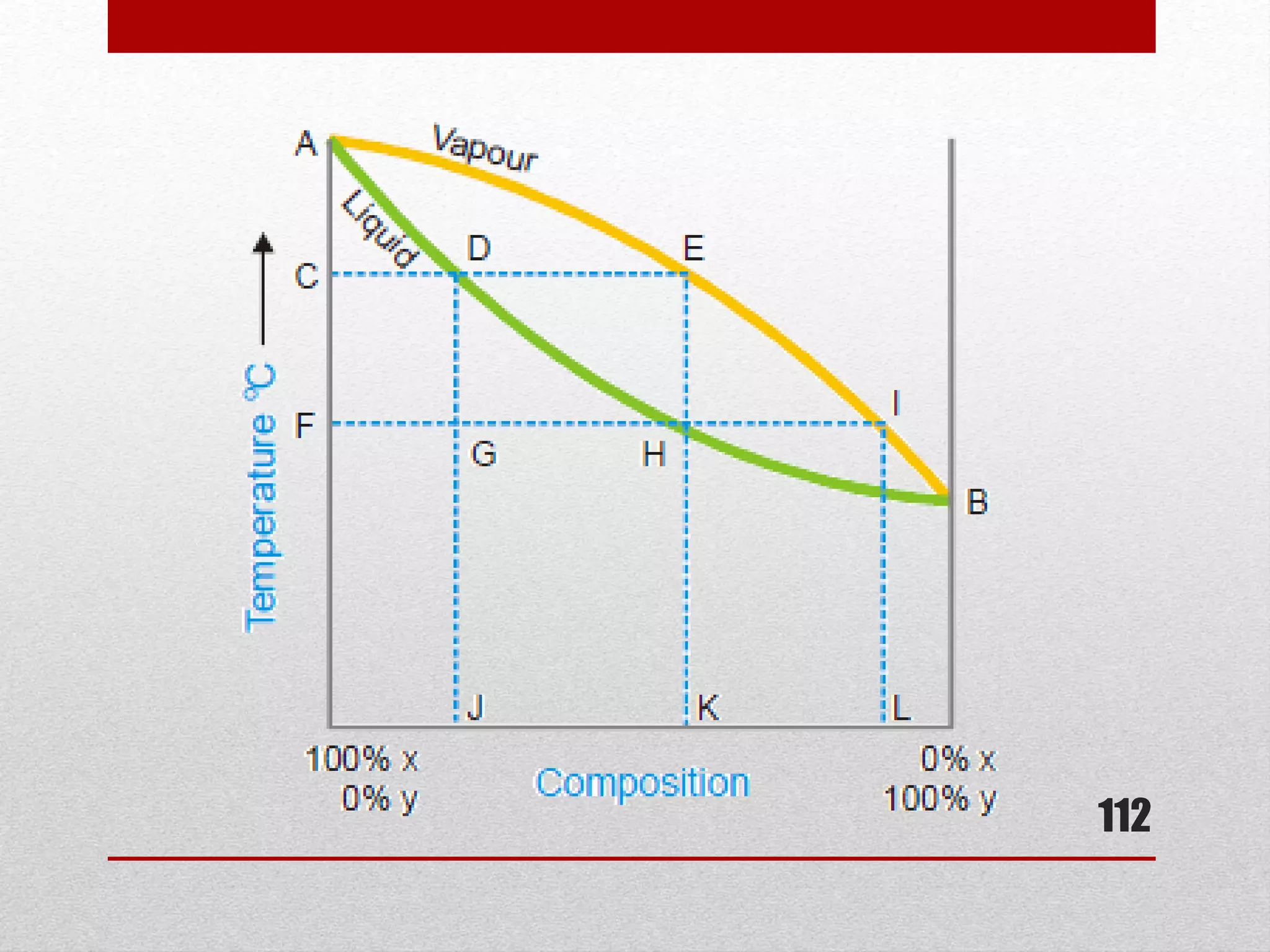
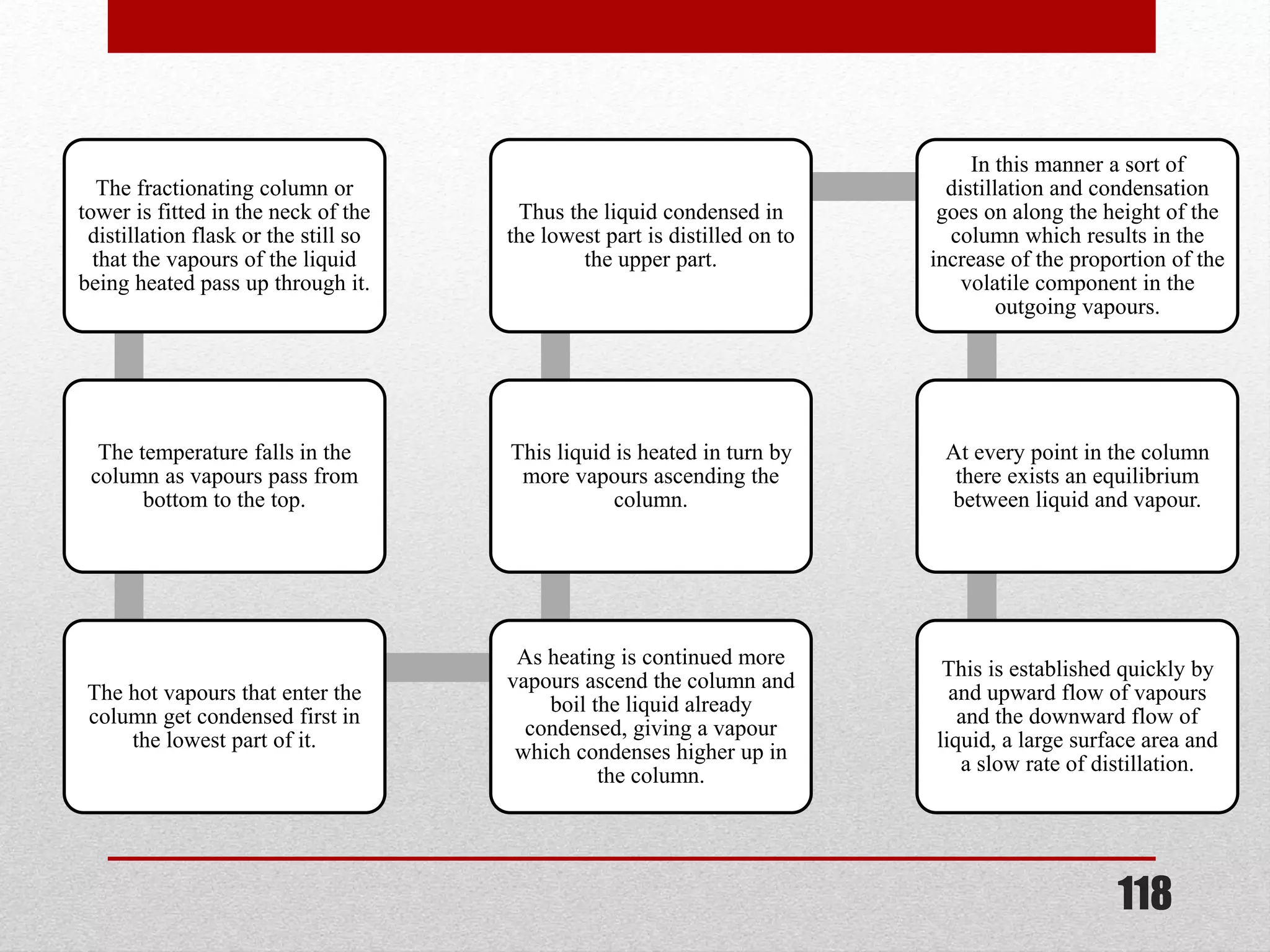
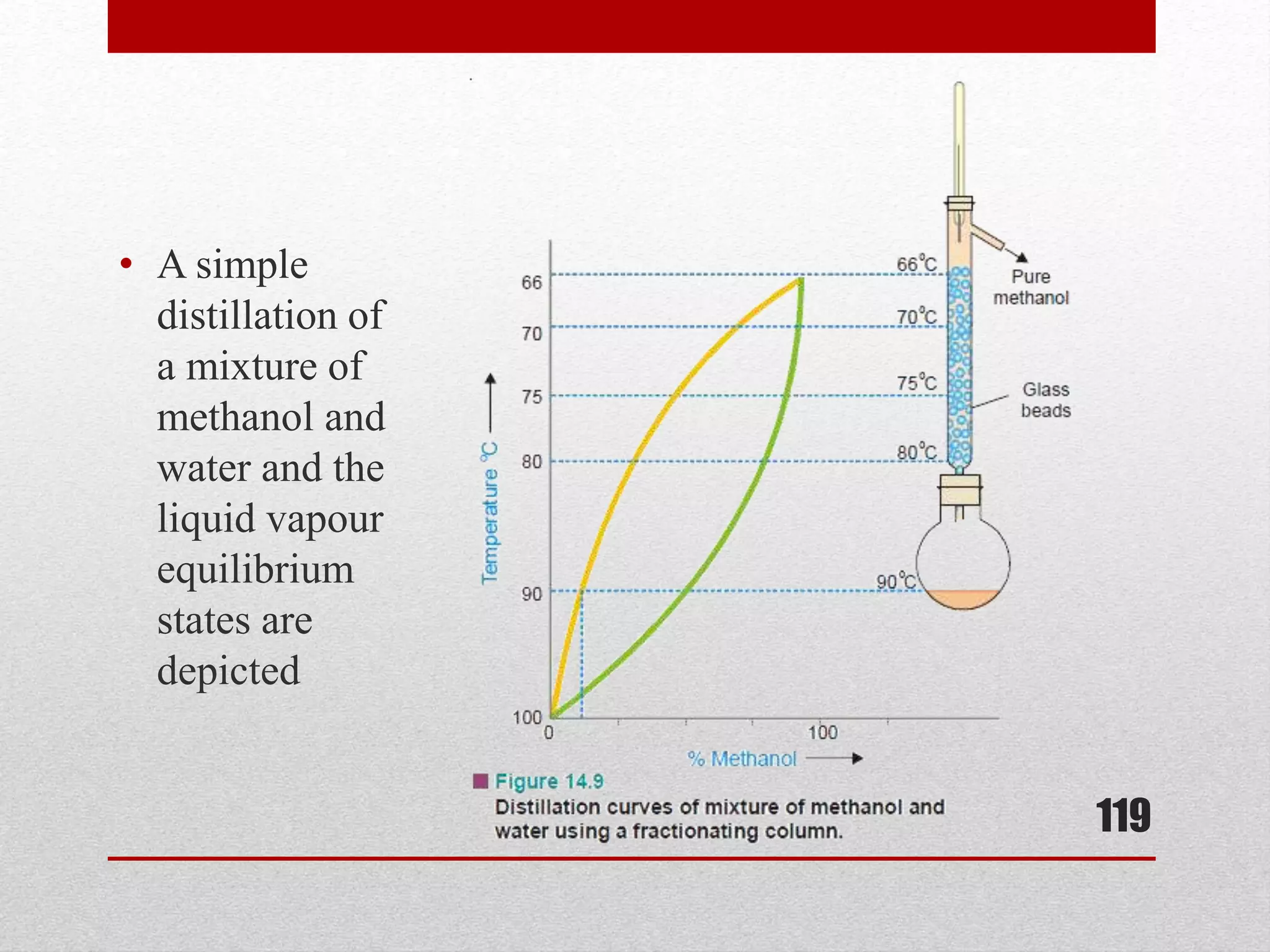
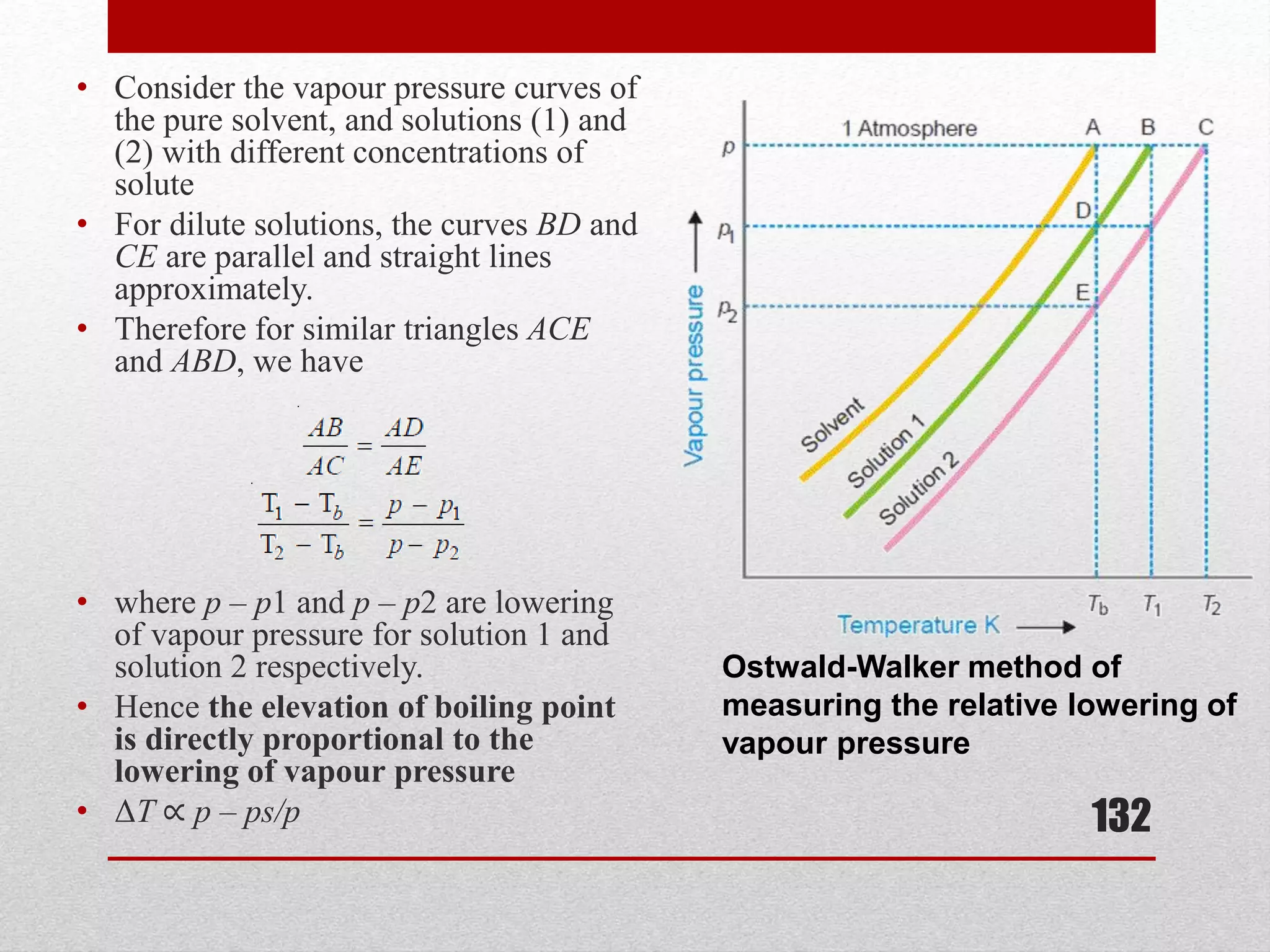
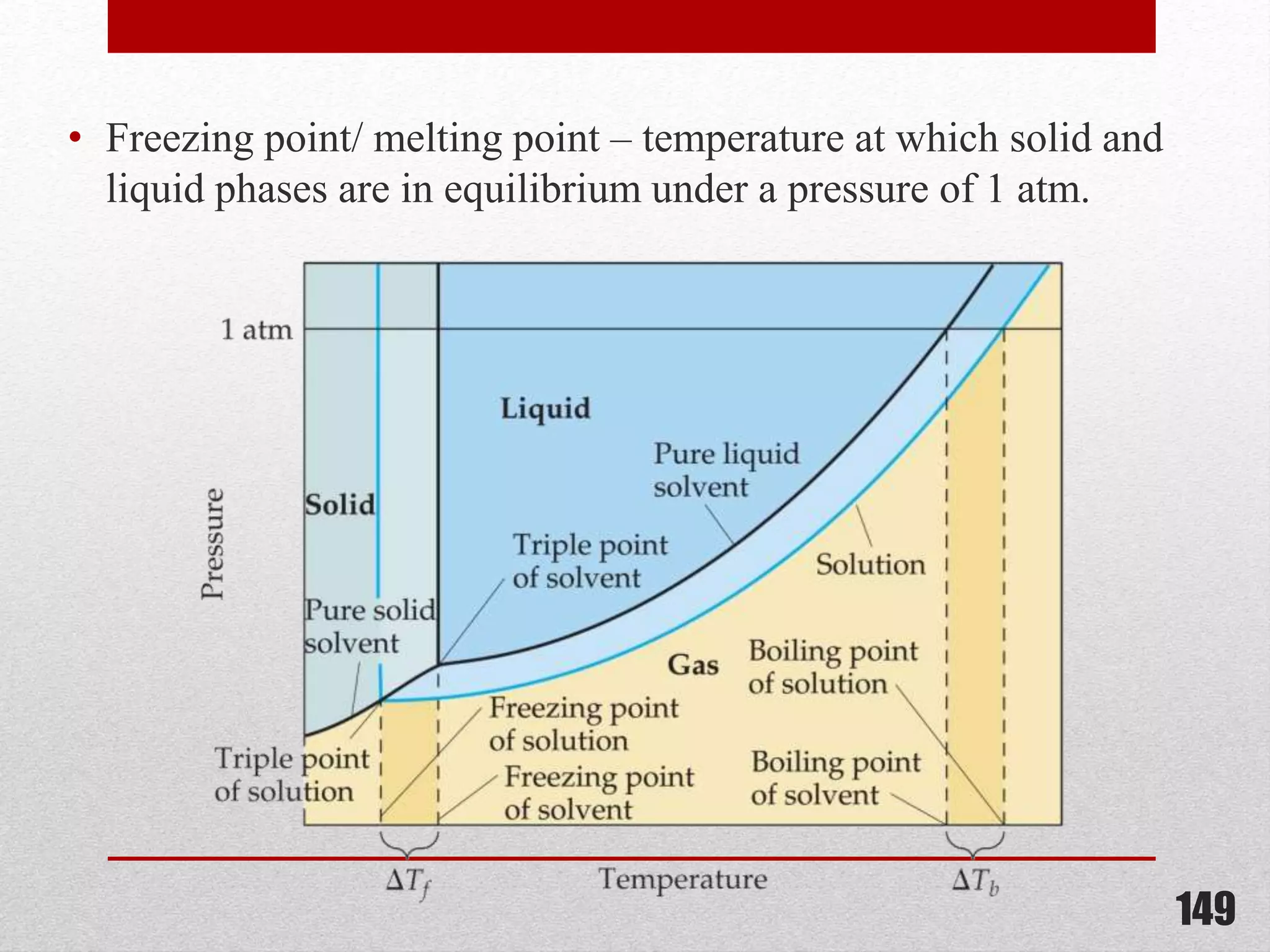
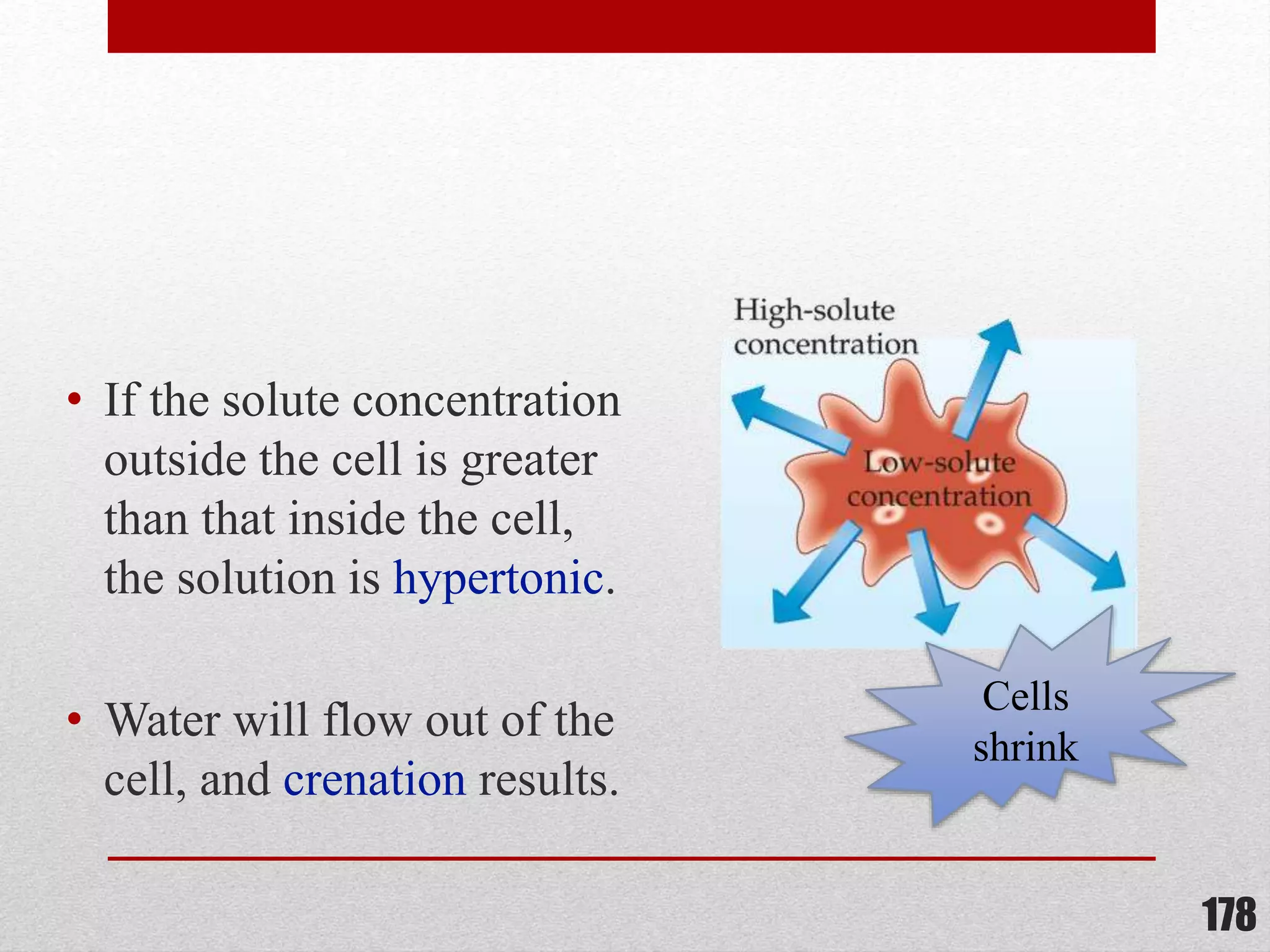
This document provides information on solutions of non-electrolytes. It defines key terms like solute, solvent, saturated solution, and supersaturated solution. It explains how a solution forms via a 3 step process of solute separation, solvent separation, and solute-solvent interaction. Various methods of expressing concentration are described, including mass percentage, parts per million/billion, mole fraction, molarity, molality, and normality. Raoult's law and its limitations are discussed. Real solutions that deviate positively or negatively from Raoult's law are explained. Henry's law relating gas solubility to partial pressure is also summarized.