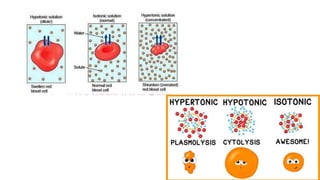
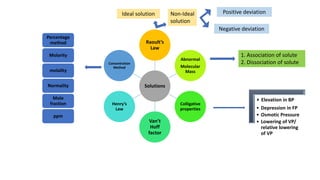
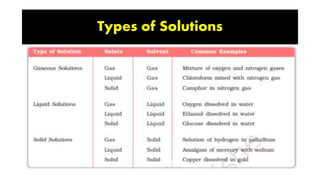
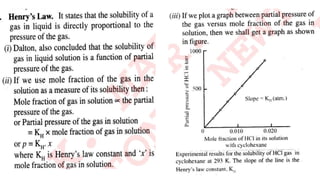
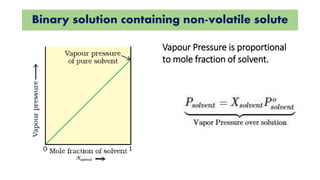
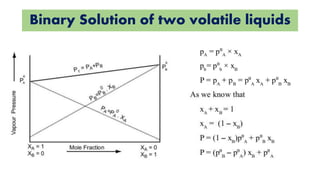
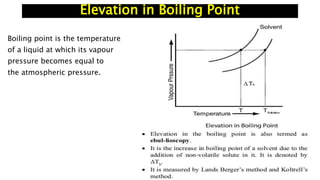
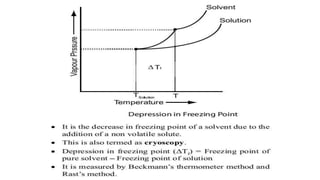
The document discusses various topics related to solutions and colligative properties. It defines key terms like solute, solvent, concentration methods. It explains concepts such as Raoult's law, deviations from Raoult's law, ideal and non-ideal solutions. It also covers colligative properties including elevation in boiling point, depression in freezing point, osmotic pressure and lowering of vapour pressure. It discusses abnormal molecular masses that can arise from solute dissociation or association and how the van't Hoff factor can explain this.

1. Solutions
Chemistry
Class 12
Chapter 2
Sheikh Khalida
Chemistry Teacher
khalidasheikh338@gmail.com

2. Solution- mixture of two or more component
• Solute- component present in smaller proportion
• Solvent- component present in larger proportion
Solution can be solid, liquid or gas
Binary solution- 2 components
Ternary solution- 3 components
Important Terms

3. Important Terms
• Aqueous solution - solute dissolved in water
• Non-aqueous solution – Solute dissolved in solvent
other than water
• Miscible liquids- mix with each other
• Immiscible liquids- do not mix with each other
• Homogeneous solution- have one phase

4. Types of Solutions

5. Concentration of Solution
Amount of substance dissolved in a specific amount of solvent at a
given temperature

6. • Percentage method
• Mole fraction
• ppm
• Molarity
• Molality
• Normality
Methods to express concentration of
solutions

7. Methods to express concentration of
solutions

23. Vapour Pressure of a Liquid
• Vapour pressure is the pressure exerted by vapours when they
are in equilibrium with the liquid phase at a given temperature. It
depends on the nature of the liquid and temperature.
• Vapour pressure of a liquid helps us to have an idea of forces of
attraction between the molecules of a liquid. More the force of
attraction, lower is the vapour pressure
and vice versa.
• Vapour pressure of a liquid increases
with increase in temperature due to
increase in kinetic energy of molecules.

24. Vapour Pressure of a Solution
• When a miscible solute is added to a pure solvent, it results in
the formation of solution. As some molecules of solute replace
the molecules of the solvent from the surface, the escaping
tendency of solvent molecules decreases. This causes a
lowering of the vapour pressure.
• The vapour pressure of a solution is less than that of pure
solvent.
• If the vapour pressure of a solvent is p° and that of solution is
ps then, lowering of vapour pressure = p° – ps.
• The vapour pressure of a solution decreases as the surface
area occupied by the solvent molecules decreases and density
increases.

26. Introduction
In the 1880s, French chemist François-Marie Raoult found out that
when a substance is dissolved in a solution, the vapour pressure
of the solution will generally decrease.
This observation depends on two variables:
1. mole fraction of the component
2. original vapour pressure (pure component)
To explain this phenomenon, Raoult proposed a law called
“Raoult’s Law”

27. What is Raoult’s Law?
Raoult’s law states that-
For a solution of volatile liquids, the partial vapour pressure of each
component of the solution is equal to the vapour pressure of that pure
component multiplied by its mole fraction in the solution.
• Mathematically, Raoult’s law equation is written as-
pcomponent = xcomponent p0
component
Where, pcomponent = partial vapour pressure of component
xcomponent = mole fraction of the component
p0
component = vapour pressure of the pure component

28. Binary solution containing non-volatile solute
Vapour Pressure is proportional
to mole fraction of solvent.

29. Binary Solution of two volatile liquids

30. Limitations of Raoult’s Law
There are few limitations to Raoult’s law.
• Raoult’s law is apt for describing ideal solutions. However, ideal solutions
are hard to find and they are rare.
• Many of the liquids that are in the mixture do not have the same
uniformity in terms of attractive forces, these type of solutions tends to
deviate away from the law.
• It is not applicable to solutes which dissociate/associate in the particular
solution.
There is either a negative or a positive deviation.

31. Ideal Solutions
• Ideal solutions are the solutions in which solute solute
and solventsolvent interactions are almost similar to
solute solvent interactions (A – B = A – A or B – B
interactions).
• Such solutions satisfy the following requirements:
1.They obey Raoult’s law for all ranges of concentrations and
temperature.
2.ΔH (mix) = 0
3.ΔV (mix) = 0
4.No dissociation or association takes place here.
5.No chemical reaction between solute and solvent.
6.It does not form azeotrope mixture.

32. • Examples:
1.Benzene + toluene
2.Hexane + heptane
3.Ethyl bromide + ethyl iodide
4.Chlorobenzene + bromobenzene
5.CCl4 + SiCl4
6.All dilute solutions

33. • Non-Ideal Solutions
Nonideal solutions are the solutions in which solute solvent interactions are
different from solute solute and solvent solvent interactions. These solutions do
not obey Raoult’s law for all concentrations and
1.ΔH (mix) ≠ 0
2.ΔV (mix) ≠ 0
• Types of non-ideal solutions
(a) Non-ideal solutions showing positive deviations:
Examples:
1.Acetone + carbon disulphide,
2.Acetone + benzene
3.Carbon tetrachloride + chloroform or Toluene
4.Methyl alcohol + water
5.Acetone + C2H5OH

34. Deviations from Raoult’s Law
• It occurs when total vapour pressure for any mole fraction is more than
what is expected according to Raoult’s law. This happens when the new
interactions are weaker than the interaction in the pure component
A-A / B-B > A-B
• It forms minimum boiling azeotropes, for example, C2H5OH +
cyclohexane. The Bonding present in pure C2H5OH is cut off on adding
cyclohexane. For such solution, ΔV and ΔH are positive.

35. Deviations from Raoult’s Law
(b) Non-ideal solutions showing negative deviations: Negative
deviation occurs when total vapour pressure for any mole fraction is less
than what is expected according to Raoult’s law.
This happens when the new interactions are stronger than the
interaction in the pure component
A-A / B-B < A-B
• It forms maximum boiling azeotrope, for example, CHCl3+ CH3COCH3.For such
solutions, ΔV and ΔH are negative.
• Examples:
• Chloroform + benzene or diethyl ether
• Acetone + aniline
• Nitric acid (HNO3) + water
• Acetic acid + pyridine

36. Azeotropic Mixture
• An azeotropic mixture is a mixture of two liquids having the same boiling point.
• These two liquids cannot be separated by simple distillation because of
similar boiling point of the liquids.
• These mixtures are thus called constant boiling mixtures.
• These are formed by non-ideal solutions.
An example of a positive azeotrope is 95.63% ethanol and 4.37% water (by mass), which boils at
78.2 °C. Ethanol boils at 78.4 °C, water boils at 100 °C, but the azeotrope boils at 78.2 °C, which is
lower than either of its constituents.
An example of a negative azeotrope is hydrochloric acid at a concentration of 20.2% and 79.8%
water (by mass). Hydrogen chloride boils at −84 °C and water at 100 °C, but the azeotrope boils at
110 °C, which is higher than either of its constituents.

37. Mixture Showing ideal behaviour or zeotropic mixture
• Those liquid mixtures which distil with a change in composition are called zeotropic
mixture.
• For this type of containing liquids A and B, vapour pressure composition curve is a
straight line. On distillation, A being more volatile, will collect as distillate.
• The remaining fraction will be poorer in A and richer in B. By repeating the process of
distillation again and again, we can get both the components in pure state, e.g.,
methanol water mixture.

38. Q2. Vapour pressure of solution of a
non-volatile solute is always ____.
1. Equal to vapour pressure of pure
solvent
2. Higher then vapour pressure of
pure solvent
3. Lower than vapour pressure of
pure solvent
4. constant
Q1. Partial pressure of solvent
in solution of non- volatile
solute is given by the equation
______.
1. p = p1
0 x2
2. p.x2 = p1
0
3. p.x1 = p1
0
4. p = p1
0 x1
Test Quiz

39. Use Your
Brain
Power!!!
Vapour pressure of pure A = 100 torr, moles=2.
Vapour pressure of B = 80 torr, moles = 3.
Calculate the total vapour pressure of mixture.

40. Colligative Properties
• Colligative properties are properties of a solution which depend only
on the number of particles like ions or molecules of the solute in a
definite amount of the solvent but not on the nature of the solute
These are as follows:
1.Relative lowering of vapour pressure
2.Osmotic pressure
3.Elevation in boiling point
4.Depression in freezing point

41. Relative Lowering of Vapour Pressure

42. Elevation in Boiling Point
Boiling point is the temperature
of a liquid at which its vapour
pressure becomes equal to
the atmospheric pressure.

44. Freezing Point Depression
Key Points
• The freezing point depression can be calculated using the pure solvent freezing point and the
molality of the solution.
• At the freezing point, the vapor pressure of both the solid and liquid form of a compound
must be equal.
• The freezing point of a substance is the temperature at which the solid and liquid forms are
in equilibrium.
 The freezing point of a solution is less than the freezing point of the pure solvent.
This means that a solution must be cooled to a lower temperature than the pure solvent in order
for freezing to occur.
 The freezing point of the solvent in a solution changes as the concentration of the solute in the
solution changes (but it does not depend on the identity of either the solvent or the solute(s)
particles (kind, size or charge) in the solution).

46. • The depression in freezing point depends upon the concentration of the solution.
• For dilute solutions, depression in the freezing point is directly proportional to
molality (m).
Thus, ∆Tf =Kf m
Where,
Kf = freezing point depression constant (or) molal depression constant (or) cryoscopic
constant.
Molal depression constant Kf can be defined as the depression in freezing point when
1mole of solute dissolved in 1kg of solvent.
The unit for Kf is kelvin kilogram /mole.
As Kf depends upon the nature of the solvent, its value is different for different
solvents.

47. • If w2 grams of a solute with molar mass M2 is dissolved in w1 grams of a
solvent, then molality m of the solution is given by -
Molarity , m = (W2 x 1000)/(W1xM2) ---(1)
ΔTf = Kf m -----(2)
ΔTf = (Kf x W2 x 1000)/(W1xM2)
M2 = = (Kf x W2 x 1000)/(W1xΔTf)
Thus, the molar mass of a non-ionic solute can be calculated by using the
depression in freezing point.

48. Important applications of depression in freezing point:
• Running a car in sub-zero temperatures even when the
radiator is full of water is possible due to the fact that a
depression in the freezing point of water takes place when an
appropriate amount of solute (ethylene glycol) called anti-freeze
is dissolved in it.
• The addition of the solutes like Sodium chloride depresses the freezing point
of water to such an extent that it cannot freeze at the prevailing temperature
and hence the snow melts off easily.
• Salt is best put on the roads before they freeze or before
snow arrives. Then, as snow falls, the salt mixes with it,
lowering its freezing point. The result is a brine solution,
preventing subsequent ice forming.

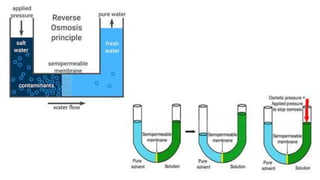
49. Osmosis
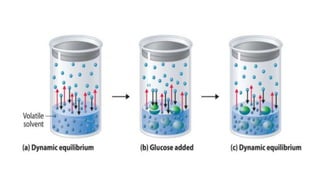
In osmosis, there is a net flow of solvent molecules from the solvent to the solution
OR
from a less concentrated solution to a more concentrated solution across a
semipermeable membrane (membranes of animal origin, membranes made from
Cu2 [Fe (CN) 6], Ca3 (PO4)2 etc.)
• Osmosis was first observed by
Abbe Nollet in 1748.
Jean-Antoine Nollet (1700-1770) was a French
clergyman and physicist who did a number of
experiments with electricity and discovered osmosis

50. Osmotic Pressure
• Osmotic pressure is the equilibrium hydrostatic pressure of the column set up as a
result of osmosis.
(Hydrostatic Pressure: Hydrostatic pressure is the pressure at any point of a
non-flowing liquid due to the force gravity.
Osmotic Pressure: Osmotic pressure is the pressure required to prevent a
solution from undergoing osmosis.)
• It is the minimum pressure that must be applied on the solution to
prevent the entry of the solvent into the solution through the semi-
permeable membrane.
• It is the minimum pressure needed to apply on a solution to make its
vapour pressure equal to vapour pressure of the solvent.
• It is denoted by P or π.
• It is measured by Pfeiffer’s method, BerkelyHartley’s method, Townsend’s
method.

52. Van’t Hoff equation of osmotic pressure/ van’t Hoff general solution
equation
Van’t Hoff – Boyle’s law
( T- constant)
Van’t Hoff – Charle’ law
(C- constant)
Combining,
Here, π = Osmotic pressure
C = Concentration of solution in mol/L
S or R = Solution constant (Value of S is same as R,
gas constant )
T = Absolute temperature in Kelvin

53. where g is the acceleration due to gravity of
that place.
This equation is used to calculate
the pressure exerted by any fluid at certain
depth h.

55. Abnormal Molecular Mass
• The theoretical values of molecular mass, when calculated from the
colligative properties of solutions, are sometimes found to differ from the
experimentally obtained values. These values are often referred to as
abnormal molar masses.
• when electrolyte solutes are dissolved in a solvent they dissociate into ions.
Since colligative properties depend only on the number of solute particles,
the dissociation of solute molecules into ions results in an increase in the
number of particles and hence affects the colligative properties.
• When 1 mole of NaCl is dissolved in 1 Kg of water, if all the molecules of
NaCl dissociate in water, there will be 1 mole of Cl– ions and 1 mole of
Na+ ions in the resulting solution (a total of 2 moles of ions in the solution).
But while calculating the molar mass using the colligative properties, we
consider only 1 mol of NaCl to be present in the solution.

56. Abnormality in the molecular mass can be explained as
follows:
• dissociation of solute molecules  increase in the number of
particles  increases the colligative properties of the solution.
• Since the molar mass is inversely proportional to the colligative
properties, its value tends to be lower than expected.
• solute particles associate  number of particles in the solution
decreases  decrease in the colligative properties.
• In this case, the molar mass values obtained are higher than
expected.

57. van’t Hoff Factor
• Certain solutes which undergo dissociation or association
in solution are found to show abnormal molecular mass.
• Due to this, the colligative property becomes abnormal
which can be explained by van’t Hoff factor.
• To obtain the colligative properties of electrolyte
solutions by using relations for non-electrolytes, van’t
Hoff suggested a factor, i , to express the extent of
dissociation or association of solute.
• This factor is named after the Dutch physical chemist Jacobus
Henricus Van’t Hoff, who won the first Nobel Prize in chemistry.

59. Knowledge, not information
Learning, not studying
Development, not progress

60. Percentage
method
Molarity
molality
Normality
Mole
fraction
ppm
Solutions
Raoult’s
Law
Abnormal
Molecular
Mass
Colligative
properties
Van’t
Hoff
factor
Henry’s
Law
Concentration
Method
Elevation in BP
• Depression in FP
• Osmotic Pressure
• Lowering of VP/
relative lowering
of VP
1. Association of solute
2. Dissociation of solute
Ideal solution Non-Ideal
solution
Positive deviation
Negative deviation