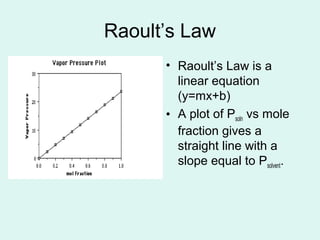
Raoult's law describes the behavior of ideal solutions. It states that the vapor pressure of a solution is proportional to the mole fraction of the solvent in the solution. The vapor pressure of a solution is lower than that of the pure solvent due to the presence of nonvolatile solute particles. This lowering of vapor pressure leads to boiling point elevation and freezing point depression in solutions, as described by the colligative properties. The quantitative relationships for boiling point elevation and freezing point depression involve the molal concentration of the solute.

1. Raoult’s Law
Pro. Dr. Syed Farman Ali Shah
Chairman
Chemical Engineering
Department

2. Raoult's Law
• The common mathematical statement for
this behavior is known as Raoult's Law:
• Psoln = Xsolvent Psolvent
• Psoln is the observed vapor pressure of the
solution
• Xsolvent is the mole fraction
• Psolvent is the vapor pressure of the pure
solvent.

3. Raoult’s Law
• From Raoult’s law we see clearly that
the amount of change in the vapor
pressure is dependent on the amount
of the nonvolatile solute added to the
solution (mole fraction) not the quality
of the solute.

4. Raoult’s Law
• Raoult’s Law is a
linear equation
(y=mx+b)
• A plot of Psoln vs mole
fraction gives a
straight line with a
slope equal to Psolvent.

5. Vapor Pressure
• The pressure of the
vapor present.
• Vapor is the liquid
molecule in gas form
over the liquid
surface.
• Remove the liquid
and you have a gas!

6. Vapor Pressure of Solutions
• In a closed container at
constant temperature
an equilibrium vapor
pressure is
established.
• The picture on the left
indicates that vapor
molecules leave a
solvent to dilute a
solution. Why?

7. Vapor Pressure of Solutions

8. Vapor Pressure of Solutions
• The vapor pressure of a liquid is much
different in a solution than it is in a pure
liquid.
• The dissolved nonvolatile solute lowers
the vapor pressure of a solvent.
• The solute decreases the number of
solvent molecules per unit volume
lowering the tendency for the molecules to
escape into vapor.

9. Vapor Pressure of Solutions
• In a solution that is half nonvolatile
solute particles and half solvent, one
would expect a vapor pressure of 1/2
the pure solvent, since only half as
many molecules can escape.
• That is what is exhibited by such a
solution.

10. Ideal Solutions
• Liquid-liquid solutions that obey Raoult’s
Law are called ideal solutions.
• For solutions that contain volatile solutions
a modified Raoult’s Law.
• Ptotal = Pa + Pb = XaP°a +XbP°b
• Pa and Pb are the partial pressure of the
two liquids in solution.
• P°a and P°b are the partial pressure of the
pure solvent.
• X is the mole fraction.

11. Nonideal Solutions

12. Problems
• A solution is prepared by mixing 5.81 g
acetone (C3H6O, molar mass =58.1 g/mol)
and 11.9 g chloroform (HCCl3, molar
mass=119.4 g/mol). At 35°C, this solution
has a total vapor pressure of 260 torr. Is
this an ideal solution? The vapor
pressures of pure acetone and pure
chloroform at 35°C are 345 and 293
respectively.

13. Solution
• Ideal solutions follow Raoult’s Law.
• Moles of each volatile liquid:
• 5.81 g acetone/58.1 g/mol = 0.100 mol
ace
• 11.9 g chloro/119 g/mol= 0.100 mol chloro
• Equal number of moles thus mole fraction:
Xa = 0.500 Xc= 0.500
• Ptotal=(0.500)(345torr) +(0.500)(293 torr)
• Ptotal= 319 torr expected

14. Discussion
• Since the observed vapor pressure is 260
torr and the calculated vapor pressure is
319 torr, this is not an ideal solution.
• Why is the vapor pressure lower?
• IMF’s: both molecules have a dipoles and
these interactions reduce the molecules
tendency to escape. This lowers the
vapor pressure more than expected.

15. Colligative Properties
• These properties are known as the
colligative properties of solutions
(collected properties) and they are:
• vapor pressure lowering
• boiling point elevation
• freezing point depression
• osmotic pressure elevation

16. Boiling point Elevation
• Boiling occurs when the vapor
pressure of a liquid equals
atmospheric pressure. But since the
vapor pressure of a solution is always
lower than that of the pure solvent,
more heat will need to be applied to
raise it to atmospheric pressure.

17. Boiling Point Elevation
• The quantitative relationship which
describes this behavior looks like this:
• ∆ Tb = Kbm
• ∆ Tb is the change in the boiling point.
• Kb is the "molal boiling point constant"
which is a property of the solvent.
• m is the molality of the solute in the
solution. Why Molality?

18. Boiling Point Elevation

19. Freezing Point Depression
• When you add salt to ice the ice melts and
the temperature of the solution drops.
The resulting solution will not freeze at 0
°C.
• Salt water has a lower vapor pressure
than pure water.
• Another way to look at it, is the particles
interfere with the water molecules’ ability
to form a crystal. The freezing point is
depressed.

20. Freezing Point Depression

21. Freezing Point Depression
• ∆ T=Kfm
• Where ∆ T is the freezing point
depression, the change in freezing point
between the pure solvent and the solution.
• Kf is the molal freezing point constant.
Values depend on the solvent.
• m is the molality of the solute in the
solution