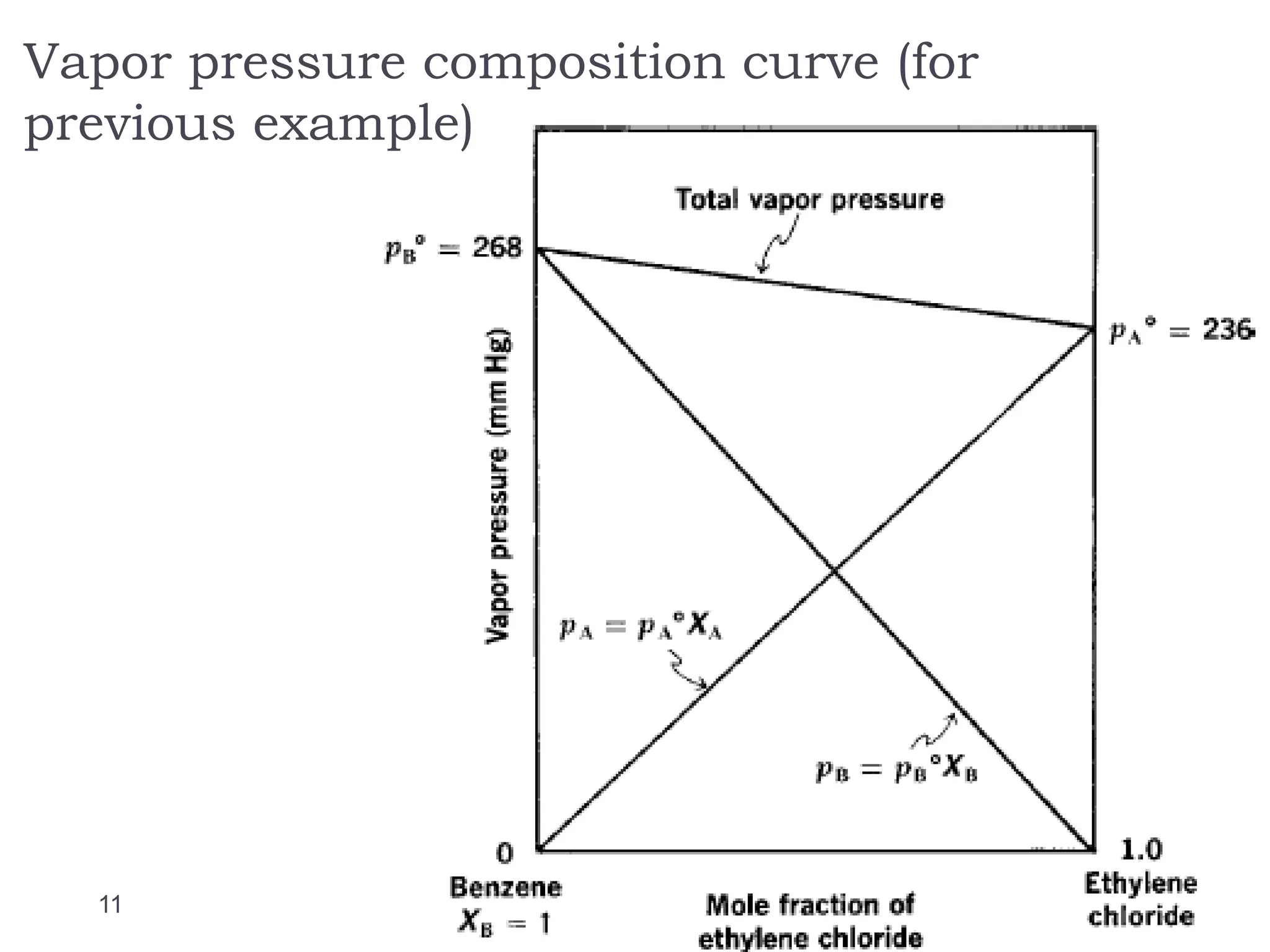
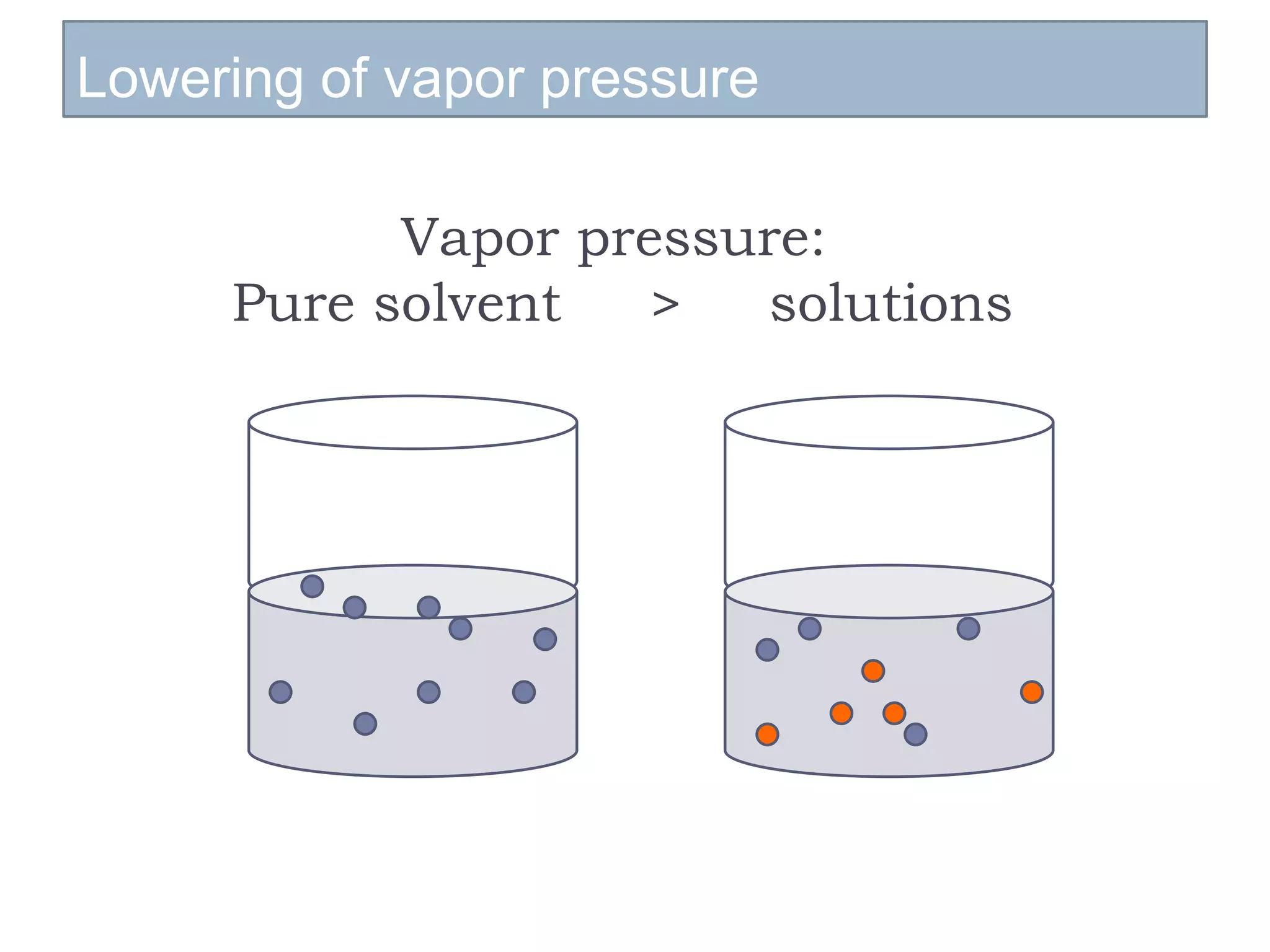
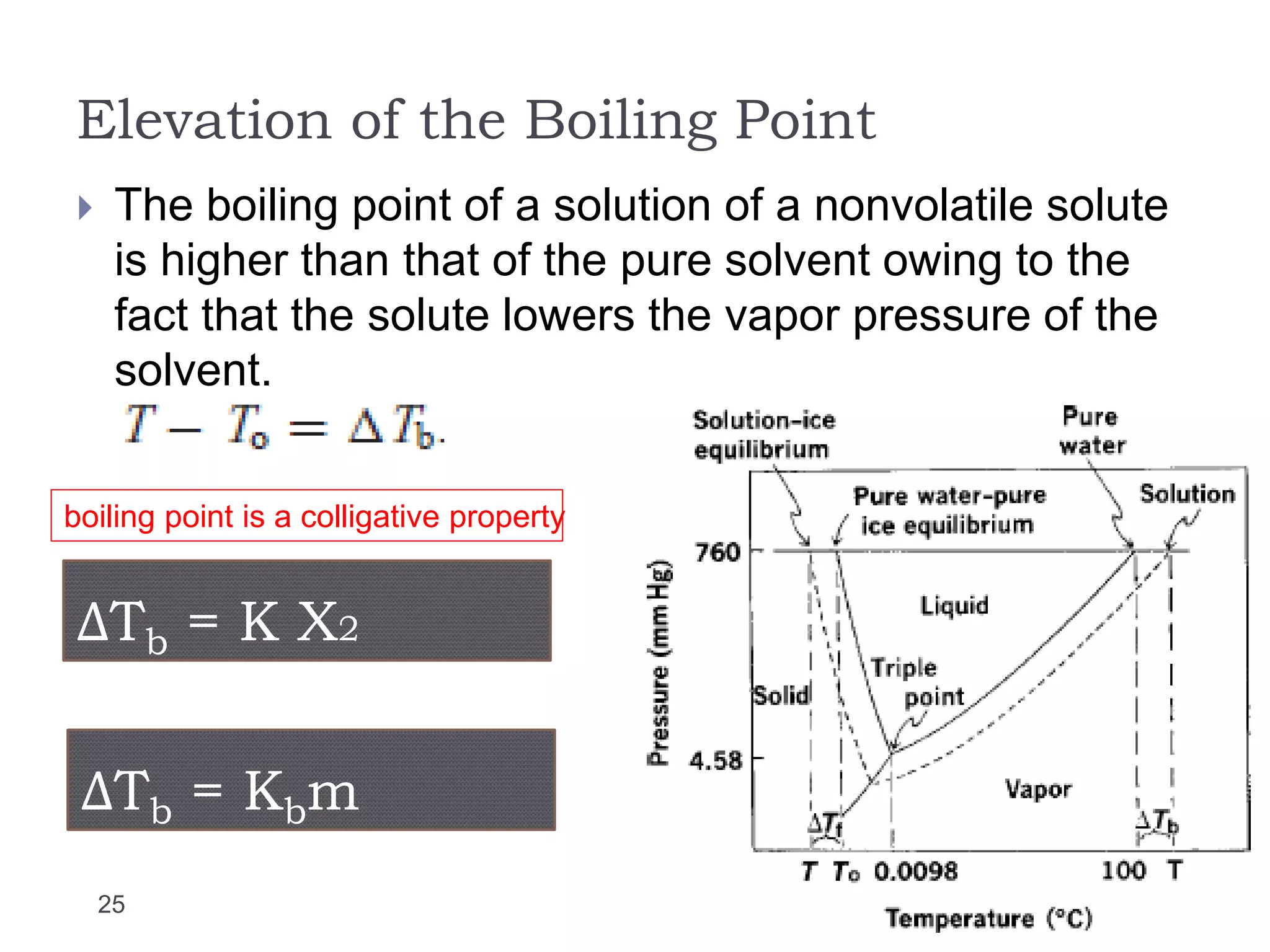
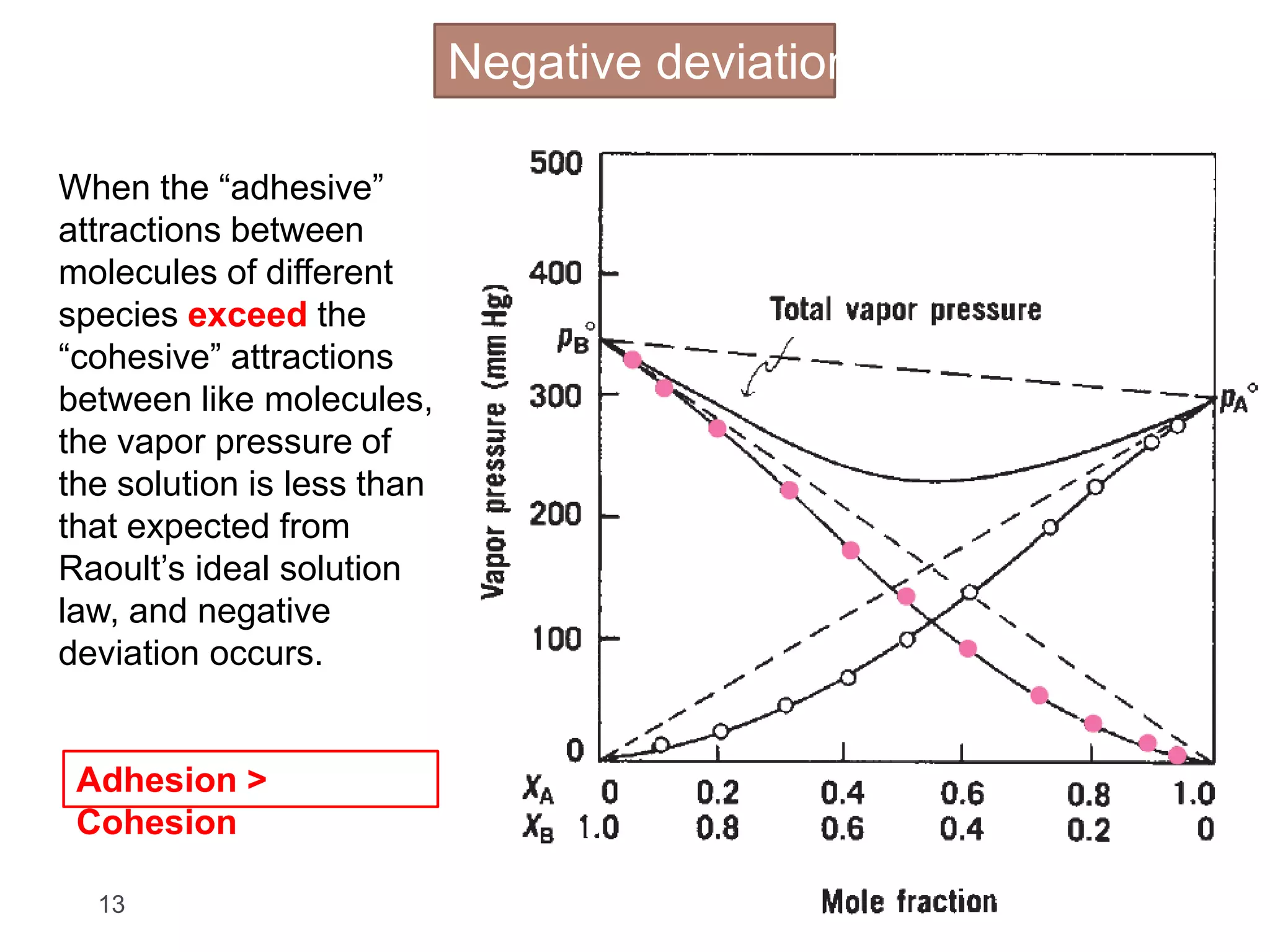
This document discusses various topics in physical pharmacy and solutions, including: - Types of solutes such as electrolytes and non-electrolytes. - Expressions used to quantify concentration in solutions such as molarity, molality, and mole fraction. - Factors that influence vapor pressure, boiling point, and freezing point of solutions. - The concept of ideal and real solutions in relation to Raoult's law and deviations from ideal behavior. 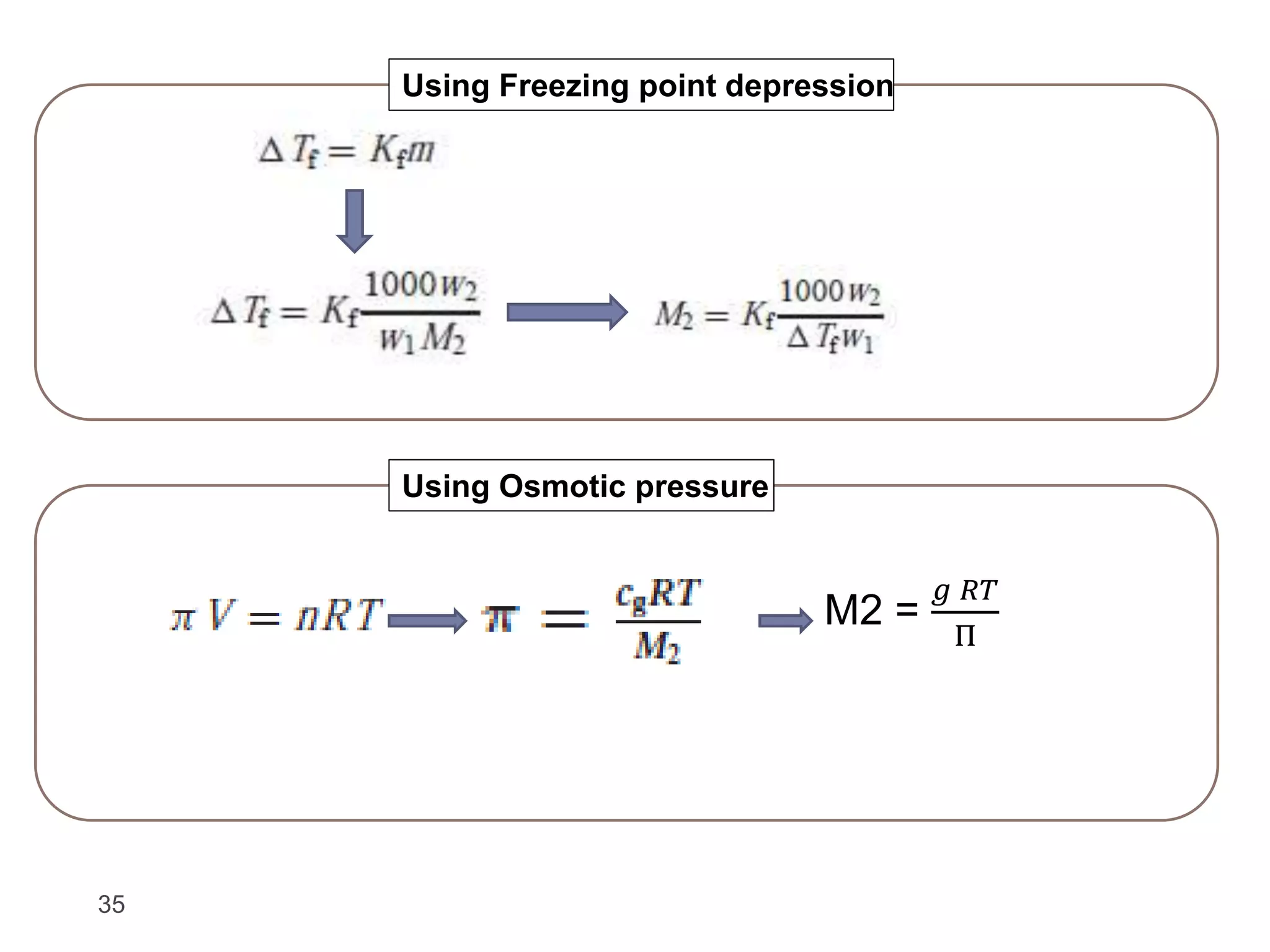- Colligative properties of solutions that depend only on the number of solute particles, including vapor pressure lowering, boiling point elevation, freezing point depression, and osmotic pressure.

1. Khalid T Maaroof
MSc. Pharmaceutical sciences
School of pharmacy – Pharmaceutics department
1
Online access: bit.ly/physicalpharmacy
Solutions
Physical Pharmacy
10/31/2015

2. Solutions
2

3. Types ofsolutes
Na+
Cl-
• Electrolytes (Conductive):
Dissociation in to ions in
solution
Eg: NaCl
• Nonelectrolytes (no conductivity):
no dissociation
Eg: suger

4. Concentration expressions for solutions
4
 Molarity?
 Normality?
 Molarity?
 Mole fracction?
 Mole percent?
 Percent
 Percent by weight % w/w
 Percent by volume %v/v
 Percent weight in volume % w/v

5. Concentration expressed as percentage
5
– Percent weight-in-weight (w/w) is the grams of solute in
100 grams of the solution.
– Percent weight-in-volume (w/v) is the grams of solute in
100ml of the solution.
– Percent volume-in-volume (v/v) is the milliliters of solute
in 100ml of the solution.
A 20 % w/w solution contains 20g solute how many grams the solvent is?

6. Molarity, Normality, and Molality
6
 Molarity and normality both depend on the volume of
the solvent, so their values are affected by change of
volume caused by factors such as change in
temperature.
 Molality doesn’t has this disadvantage.

7. Mole fraction
7
 In a solution containing 0.01 mole of solute and 0.04
mole of solvent, the mole fraction of the solute is 0.2
and for solvent it is 0.8
Mole percent = mole fraction X 100

8. 8
 An aqueous solution of ferrous sulfate was prepared
by adding 41.50 g of FeSO4 to enough water to
make 1000 mL of solution. The density of the
solution is 1.0375 and the molecular weight of
FeSO4 is 151.9.
Calculate
 (a) molarity
 (b) molality
 (c) mole fraction of FeSO4, mole fraction of water,
and the mole percent of the two constituents
 (d) % w/w of FeSO4.

9. Ideal and real solutions
9
 Ideal solution is defined as a solution in which there is
no change in the properties of the components other
than dilution when they are mixed to form the solution
 Molecules exhibit complete freedom of motion and
randomness of distribution in the solution.
 Ideality in solutions means complete uniformity of
attractive forces

10. Ideal Solutions and
10
 P = pA + pB
 pA = pA◦ XA
 pB = pB◦ XB
 What is the partial vapor pressure of benzene and of
ethylene chloride in a solution at a mole fraction of
benzene of 0.6? The vapor pressure of pure benzene at
50◦C is 268 mm, and the corresponding pA ◦ for
ethylene chloride is 236 mm.
Raoult's Law States that, in an ideal solution, the partial vapor pressure of each volatile
constituent is equal to the vapor pressure of the pure constituent multiplied by its
mole fraction in the solution. Thus, for two constituents A and B,

11. 11
Vapor pressure composition curve (for
previous example)

12. Real Solutions
12
 Ideality in solutions presupposes complete uniformity
of attractive forces.
 Many examples of solution pairs are known,
however, in which the “cohesive” attraction of A for A
exceeds the “adhesive” attraction existing between A
and B.
 Similarly, the attractive forces between A and B may
be greater than those between A and A or B and B.
 Such mixtures are real or nonideal; that is, they do
not adhere to Raoult’s law
 Two types of deviation from Raoult’s law are
recognized, negative deviation and positive

13. 13
When the “adhesive”
attractions between
molecules of different
species exceed the
“cohesive” attractions
between like molecules,
the vapor pressure of
the solution is less than
that expected from
Raoult’s ideal solution
law, and negative
deviation occurs.
Negative deviation
Adhesion >
Cohesion

14. 14
When the “adhesive”
attractions between
molecules of different
species are weaker
than “cohesive”
attractions between like
molecules, the vapor
pressure of the solution
is more than that
expected from Raoult’s
ideal solution law, and
positive deviation
occurs.
Positive deviation
Adhesion <
Cohesion

15. Questions !
10/31/201515

16. Colligative properties
16

17. Colligative properties
17
 Colligative properties of solutions are those that
affected (changed) by the presence of solute and
depend solely on the number (amount of solute in
the solutions) rather than nature of constituents.
 Examples of colligative properties are:
 Vapor pressure
 Boiling point
 Freezing point
 Osmotic pressure

18. Colligative vs Non-colligative
18
Compare 1.0 M aqueous sugar solution to a 0.5 M solution of
salt (NaCl) in water.
both solutions have the same number of dissolved particles
any difference in the properties of those two solutions is due to
a non-colligative property.
Both have the same freezing point, boiling point, vapor
pressure, and osmotic pressure

19. Non-Colligative Properties
Sugar solution is sweet and salt solution is salty.
Therefore, the taste of the solution is not a colligative
property.
Another non-colligative property is the color of a solution.
Other non-colligative properties include viscosity, surface
tension, and solubility.
19

20. Lowering of vapor pressure
Vapor pressure:
Pure solvent > solutions

21. Lowering of vapor pressure
21
 According to raoult’s law Psolvent = Pºsolvent Xsolvent
 But if the solute used in non volatile only pressure from
solvent can be considered.
 So:
 On the other hand
Psolute = Pºsolute Xsolute
Psolution = Pºsolvent Xsolvent
X1 = mole fraction of solvent
X2 = mole fraction of solute

22. 22
 ∆p = p1◦ − p is the lowering of the vapor pressure
and ∆p/p1◦ is the relative vapor pressure lowering.
 The relative vapor pressure lowering depends only
on the mole fraction of the solute, X2, that is, on the
number of solute particles in a definite volume of
solution. Therefore, the relative vapor pressure
lowering is a colligative property.

23. 23
 Calculate the relative vapor pressure lowering at 20◦C
for a solution containing 171.2 g of sucrose (w2) in 100
g (w1) of water. The molecular weight of sucrose (M2)
is 342.3 and the molecular weight of water (M1) is
18.02 g/mole.

24. Boiling point elevation
24
Boiling point elevation is a colligative property related to
vapor pressure lowering.
The boiling point is defined as the temperature at which
the vapor pressure of a liquid equals the atmospheric
pressure.
Due to vapor pressure lowering, a solution will require a
higher temperature to reach its boiling point than the pure
solvent.

25. Elevation of the Boiling Point
25
 The boiling point of a solution of a nonvolatile solute
is higher than that of the pure solvent owing to the
fact that the solute lowers the vapor pressure of the
solvent.
ΔTb = K X2
ΔTb = Kbm
boiling point is a colligative property

26. 26
 In dilute solutions:
ΔTb = K X2 ΔTb = Kbm
Tb: is known as the boiling point elevation
Kb: is called the molal elevation constant.
m: is molality of solvent

27. Freezing Point
27
Every liquid has a freezing point - the temperature at
which a liquid undergoes a phase change from liquid to
solid.
When solutes are added to a liquid, forming a solution, the
solute molecules disrupt the formation of crystals of the
solvent.
That disruption in the freezing process results in a
depression of the freezing point for the solution relative to
the pure solvent.

28. Depression of the Freezing Point
28
∆T f = Tº f – T f
Kf is the molal epression constant

29. 29
What happens to the triple point?

30. 30

31. Osmotic Pressure
31
When a solution is separated
from a volume of pure solvent
by a semi-permeable
membrane that allows only the
passage of solvent molecules,
the height of the solution
begins to rise.
The value of the height
difference between the two
compartments reflects a
property called the osmotic
pressure of a solution.

32. Osmotic Pressure
32
Where
π is the osmotic pressure .
V is the volume of the solution in liters.
n is the number of moles of solute.
R is the gas constant, equal to 0.082 liter atm/mole deg.
T is the absolute temperature.
 Van't Hoff and Morse Equations for Osmotic Pressure:

33. 33

34. MOLECULAR WEIGHT DETERMINATION
34
 The four colligative properties can be used to calculate
the molecular weights of nonelectrolytes present as
solutes. Using vapor pressure lowering
Using boining point elevation

35. 35
Using Freezing point depression
M2 =
𝑔 𝑅𝑇
Π
Using Osmotic pressure

36. 36

37. 37

38. 38

39. Questions !
10/31/201539