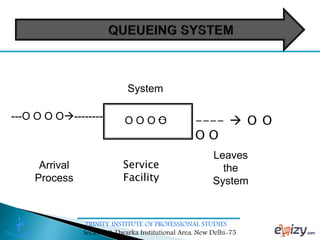
The document discusses queueing theory, focusing on the formation of queues due to limited service facilities and infinite customer arrivals. It outlines key concepts such as arrival rate, service rate, queue discipline, and various metrics like average wait time and system utilization. Additionally, it provides an example scenario involving a retail outlet to illustrate the application of the single-channel queuing model.

1. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Affiliated Institution of G.G.S.IP.U,
Delhi
Paper Id 17305
Paper code BBA 305

2. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
 The study of queues is called queueing theory.
 Queue is formed because:-
 The service facility is limited & the arrivals are
infinite.
 The mismatch between service facility & arrivals.

3. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
.
 Arrival Rate (/) - No of customers arriving to a system per
unit time
 Inter Arrival Time (1//) - The time between arrival of 2
customers in a system
 Service Rate (u) – No of units served by a server per unit
time
 Service Time (1/u)- Time taken by a server to serve a
customer
TERMINOLOGY

4. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
---O O O O---------
System
--O O O O ----  O O
O O
Arrival
Process
Service
Facility
Leaves
the
System

5. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
 According to size :-
 Finite
 Infinite
 According to pattern:-
 Individual
 Batches
 According to Inter-arrival Time:-
 Deterministic
 Stochastic

6. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
 Balking
 Reneging
 Jockeying

7. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Capacity- can either be finite or
infinite
 Size- no. of Servers
 Queue Discipline
 First Come First Serve (F.I.F.O)
 Last In Last Out (L.I.F.O)
 Service in random order (S.I.R.O)
 Priority Queue (P.Q)

8. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
 a/b/c : d/e/f
 a ----> arrival process
 b ----> service time
 c ----> no of servers
 d ----> queue discipline
 e ----> Capacity of the system
 f -----> size of calling source
 For Example:- (M/M/1) : ( F.I.F.O/infi/infi)

9. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
/ ----> arrival rate
u ----> service rate
Lq ----> Average no of customers waiting for service
Ls ----> Average no of customers in the entire system
Wq ----> Average time customers wait in queue
w ----> Average time customers spend in the system
1/u ----> Average service time
1/ / ----> Average arrival time
po ----> prob of Zero unit in the system
pn ----> prob of n units in the system
P (Row) ----> system utilization

10. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
P (Row) = / / u
Lq = P2 / 1-P
Ls = P/ 1-P
Wq = / / u(u- / )
Ws = /1 / u- /

11. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
 Probability that the service facility will be idle is given by
 P0 = 1- / / u
 Probability that there are n number of customers in the system
 (denoted by Pn is given by
 Pn = P0 (/ / u )n
 Probability that the number of customers in the queue is greater than
k is
 P( n>k)= (/ / u )k+1

12. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
 A retail outlet has a single cashier . During the rush hours,
customers arrive at a rate of 20 customers per hour. The
average number of customers that can be processed by the
cashier is 24 per hour. Assume that the conditions for use of
the single channel queuing model apply. What is the
 (a) probability that the cashier is idle?
 (b) Average no of customers in the system.
 (c) Average time a customer spends in the system
 (d) Average no of customers in the queue.

13. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75