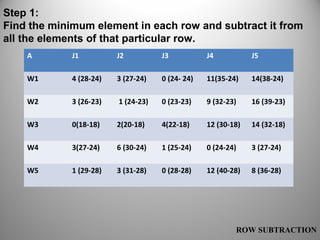
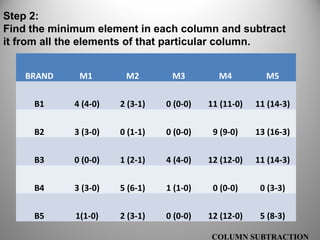
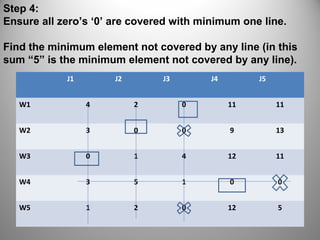
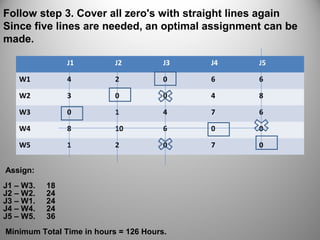
This document discusses assignment problems and how to solve them using the Hungarian method. Assignment problems involve efficiently allocating people to tasks when each person has varying abilities. The Hungarian method is an algorithm that can find the optimal solution to an assignment problem in polynomial time. It involves constructing a cost matrix and then subtracting elements in rows and columns to create zeros, which indicate assignments. The method is iterated until all tasks are assigned with the minimum total cost. While typically used for minimization, the method can also solve maximization problems by converting the cost matrix.

2. ASSIGNMENT PROBLEM
1. Gurmeet Singh, Roll No: 9
2. Jyoti Singh, Roll No: 10
3. Nakul Bhardwaj, Roll No: 15
4. Prakalp Vora, Roll No: 17
5. Vicky Shah, Roll No: 31
6. Yashwant Kharat, Roll No: 34

3. WHAT IS ASSIGNMENT PROBLEM ?
• Assignment problem refers to special class of linear
programming problems that involves determining the most
efficient assignment of people to projects, salespeople to
territories, contracts to bidders and so on.
• It is often used to minimize total cost or time of performing
task.
• One important characteristic of assignment problems is
that only one job (or worker) is assigned to one machine
(or project).

4. WHAT IS ASSIGNMENT PROBLEM ?
• Each Assignment problem has a Matrix associated with it.
• The number in the table indicates COST associated with
the assignment.
• The most efficient linear programming algorithm to find
optimum solution to an assignment problem is Hungarian
Method (It is also know as Flood’s Technique).

5. ASSIGNMENT PROBLEM USING HUNGARIAN METHOD
• The Hungarian method is a combinatorial
optimization algorithm that solves the assignment
problem in polynomial time and which anticipated
later primal-dual methods.
• It was developed and published in 1955 by Harold
Kuhn, who gave the name "Hungarian method"
because the algorithm was largely based on the earlier
works of two Hungarian mathematicians: Denes Konig
and Jeno Egervary.

6. REQUIREMENTS OF DUMMY ROWS AND
COLUMN
• To arrive at the solution, assignment problems requires
equal number of Row and Column.
• If the number of task that needs to be done exceeds the
number of resource available, dummy row or a column
just needs to be added as the case may be.
• This creates a table of equal dimensions.
• The dummy row or column is non existent . Hence the
value can be entered as Zeros.

7. Case Study:
A company has a five job to be done by 5 workers each
worker are assigned to one and only one job. Number of
hours each worker takes to complete a job is given with
A J1 J2 J3 J4 J5
W1 28 27 24 35 38
W2 26 24 23 32 39
W3 18 20 22 30 32
W4 27 30 25 24 27
W5 29 31 28 40 36

8. Step 1:
Find the minimum element in each row and subtract it from
all the elements of that particular row.
ROW SUBTRACTION
A J1 J2 J3 J4 J5
W1 4 (28-24) 3 (27-24) 0 (24- 24) 11(35-24) 14(38-24)
W2 3 (26-23) 1 (24-23) 0 (23-23) 9 (32-23) 16 (39-23)
W3 0(18-18) 2(20-18) 4(22-18) 12 (30-18) 14 (32-18)
W4 3(27-24) 6 (30-24) 1 (25-24) 0 (24-24) 3 (27-24)
W5 1 (29-28) 3 (31-28) 0 (28-28) 12 (40-28) 8 (36-28)

9. Step 2:
Find the minimum element in each column and subtract
it from all the elements of that particular column.
COLUMN SUBTRACTION
BRAND M1 M2 M3 M4 M5
B1 4 (4-0) 2 (3-1) 0 (0-0) 11 (11-0) 11 (14-3)
B2 3 (3-0) 0 (1-1) 0 (0-0) 9 (9-0) 13 (16-3)
B3 0 (0-0) 1 (2-1) 4 (4-0) 12 (12-0) 11 (14-3)
B4 3 (3-0) 5 (6-1) 1 (1-0) 0 (0-0) 0 (3-3)
B5 1(1-0) 2 (3-1) 0 (0-0) 12 (12-0) 5 (8-3)

10. Remark: Step 1 and 2 creates at least one Zero ‘0’ in
each row and Column.

11. Step 3:
Starting from 1st
row, if there is exact one zero, make an
assignment and cancel all Zero's in that column and then
draw a vertical line. Similarly, starting from 1st
column, if
there is exact one zero, make an assignment and cancel all
zero’s in that row, and then draw a horizontal line.
Continue this step till all zero’s are an assignment or
Cancelled.
J1 J2 J3 J4 J5
W1 4 2 0 11 11
W2 3 0 0 9 13
W3 0 1 4 12 11
W4 3 5 1 0 0
W5 1 2 0 12 5

12. Step 3 (Continued):
If optimal assignment is not formed go to step 4
i.e. There should be 5 straight lines.
J1 J2 J3 J4 J5
W1 4 2 0 11 11
W2 3 0 0 9 13
W3 0 1 4 12 11
W4 3 5 1 0 0
W5 1 2 0 12 5

13. Step 4:
Ensure all zero’s ‘0’ are covered with minimum one line.
Find the minimum element not covered by any line (in this
sum “5” is the minimum element not covered by any line).
J1 J2 J3 J4 J5
W1 4 2 0 11 11
W2 3 0 0 9 13
W3 0 1 4 12 11
W4 3 5 1 0 0
W5 1 2 0 12 5

14. Step 5: Subtract the element (i.e. 5) from the elements not
covered by the line. Also add the same element (i.e. 5) to the
elements which are at the intersections.
J1 J2 J3 J4 J5
W1 4 2 0 6 (11-5) 6 (11-5)
W2 3 0 0 4 (9-5) 8 (13-5)
W3 0 1 4 7 (12-5) 6 (11-5)
W4 8 (3+5) 10 (5+5) 6 (1+5) 0 0
W5 1 2 0 7 (12-5) 0 (5-5)

15. Follow step 3. Cover all zero's with straight lines again
Since five lines are needed, an optimal assignment can be
made.
Assign:
J1 – W3. 18
J2 – W2. 24
J3 – W1. 24
J4 – W4. 24
J5 – W5. 36
Minimum Total Time in hours = 126 Hours.
J1 J2 J3 J4 J5
W1 4 2 0 6 6
W2 3 0 0 4 8
W3 0 1 4 7 6
W4 8 10 6 0 0
W5 1 2 0 7 0

16. Assign:
J1 – W3 18
J2 – W2 24
J3 – W1 24
J4 – W4 24
J5 – W5 36
Minimum Total Time = 126 Hours.
Hence, the optimum solution is UNIQUE.

17. MAXIMISATION PROBLEM
• Assignment problems can also be used solve cases of
maximization model.
• For instance, Travelling Salesman problem, milk van
routings and so on.
• Problem can be solved by first subtracting the biggest
element in the problem from all other elements (i.e.
converting cost table in to opportunity loss table.).
• Later steps, are similar as the minimization problem.

18. SUMMARY
• Assignment problem deals with the problem of assigning
jobs to machines or men to jobs which are to be performed
with varying efficiency.
• It can be used to solve cases of Travelling Salesman
problem.
• It is basically a minimizing model but it can be used to
solve cases of maximization by converting cost table in to
opportunity loss table.

19. DRAWBACK OF ASSIGNMENT
PROBLEM
• Assignment becomes a problem because each job requires different skills and
the capacity or efficiency of each person with respect to these jobs can be
different. This gives rise to cost differences. If each person is able to do all jobs
equally efficiently then all costs will be the same and each job can be assigned to
any person.
• When assignment is a problem it becomes a typical optimization problem it can
therefore be compared to a transportation problem. The cost elements are given
and is a square matrix and requirement at each destination is one and
availability at each origin is also one.
• In addition we have number of origins which equals the number of destinations
hence the total demand equals total supply . There is only one assignment in
each row and each column .However If we compare this to a transportation
problem we find that a general transportation problem does not have the above
mentioned limitations. These limitations are peculiar to assignment problem
only.

20. THANK YOU!