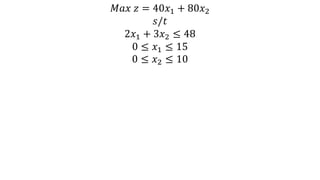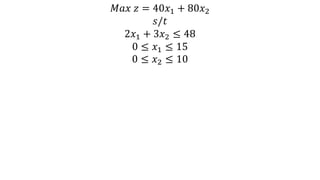
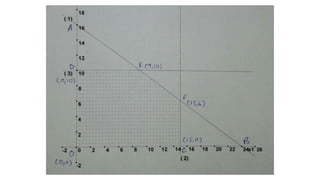
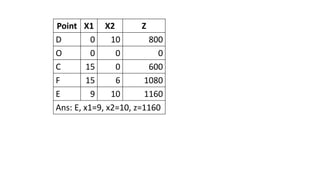
The document discusses the ABC Company's expansion into the production of AM-FM radios alongside AM radios, detailing its production capabilities and profit contributions. It formulates a linear programming model aimed at maximizing profits, given constraints on production time and sales limits. The optimal solution indicates producing 9 AM radios and 10 AM-FM radios, resulting in a maximum profit of Rs. 1160.

1. LPP Numerical Solved
2008

2. The ABC Company has been a producer of picture tubes for TV sets and
certain printed circuits for radios. The company has just expanded into full
scale production and marketing of AM-FM radios. It has built a new plant
that can operate 48 hours per week. Production of an AM radio in the new
plant will require 2 hours and production of AM-FM radio requires 3 hours.
Each AM radio will contribute Rs.40 to profits while an AM-FM radio will
contribute Rs.80 to profits. The marketing department, after extensive
research, has determined that a maximum of 15 AM radios and 10 AM-FM
radios can be sold each week. Formulate a linear programming model to
determine the optimum production mix of AM and AM-FM radios that will
maximize profits. Solve it using the graphical method and the simplex
method.

3. Formulation

4. 𝑀𝑎𝑥 𝑧 = 40𝑥1 + 80𝑥2
𝑠/𝑡
2𝑥1 + 3𝑥2 ≤ 48
0 ≤ 𝑥1 ≤ 15
0 ≤ 𝑥2 ≤ 10

5. Solution using Graphical Method

6. 𝑀𝑎𝑥 𝑧 = 40𝑥1 + 80𝑥2
𝑠/𝑡
2𝑥1 + 3𝑥2 ≤ 48
0 ≤ 𝑥1 ≤ 15
0 ≤ 𝑥2 ≤ 10

9. Point X1 X2 Z
D 0 10 800
O 0 0 0
C 15 0 600
F 15 6 1080
E 9 10 1160
Ans: E, x1=9, x2=10, z=1160