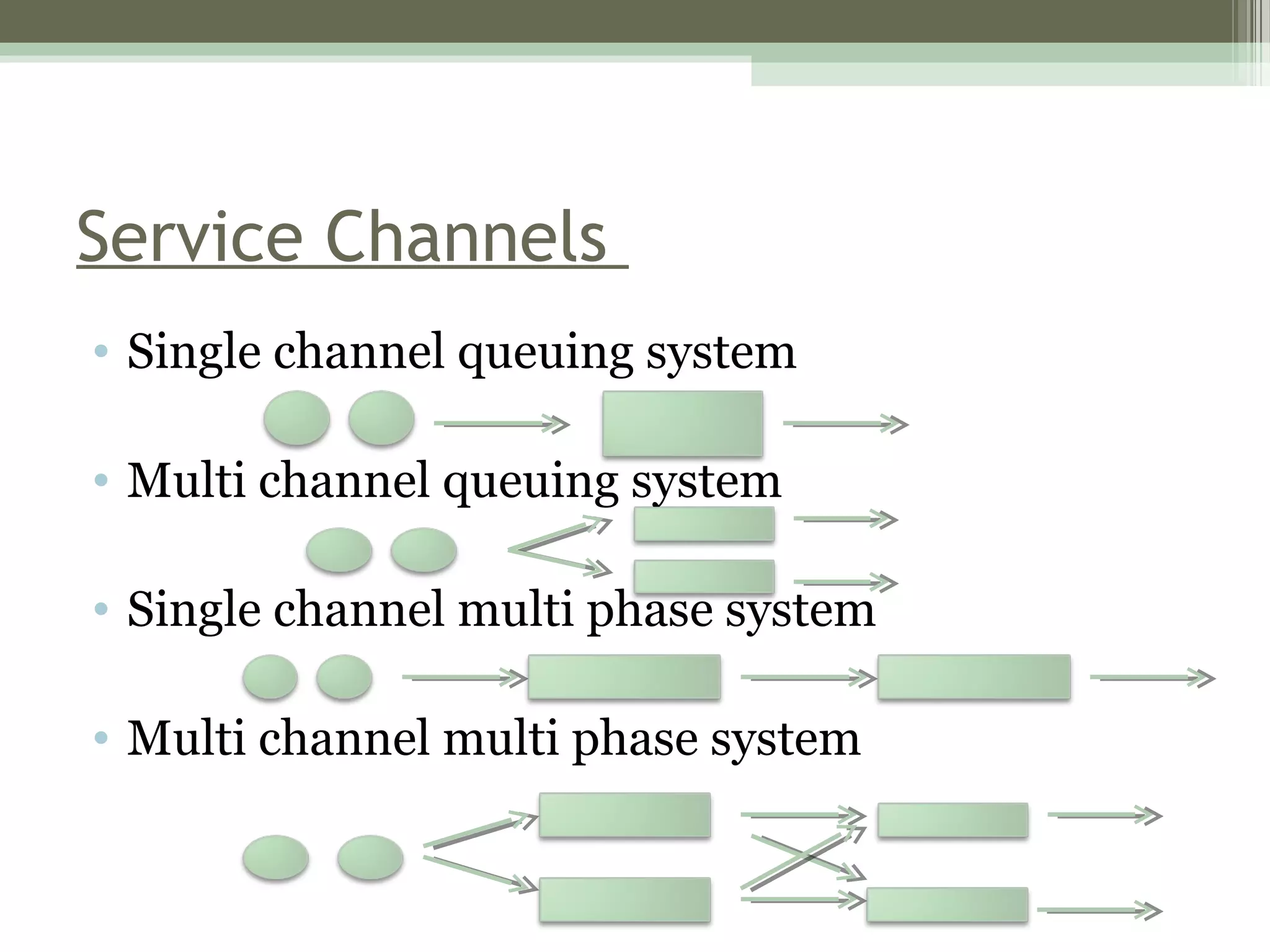
Queuing theory is used to model waiting lines in systems where demand fluctuates. It can be used to optimize resource allocation to minimize costs associated with customer wait times and unused service capacity. The key elements of a queuing system include arrivals, a queue or waiting line, service channels, and a service discipline for determining order of service. Customers arrive according to a Poisson distribution and service times follow an exponential distribution. The goal of queuing analysis is to determine the number of service channels needed to balance wait time costs and idle resource costs.

1. Presented by :
Shinki jalhotra

2. Queuing Theory
• Queuing theory is the mathematics of waiting
lines.
• It is extremely useful in predicting and
evaluating system performance.
• Queuing theory has been used for operations
research, manufacturing and systems analysis.
Traditional queuing theory problems refer to
customers visiting a store, analogous to requests
arriving at a device.

3. Queuing problems arises because either
…
There is too much demand on
the facilities
There is too less demand
(Much waiting time or inadequate
Number of service facilities)
(Much idle facility time or too
Many facilities)
The problem is to either schedule arrivals or provide extra facilities or
both so as to obtain an optimum balance between costs associated with
waiting time and idle time .

4. Basic elements of Queuing System
• Entries or customers
• Queue (waiting lines)
• Service channels or service facility

5. Basic Structure

7. Arrival pattern
•Customers arrive in
scheduled or random
fashion.
• The time duration
between each
customers’ arrival is
known as inter
arrival time. We
assume it to follow
Poisson
Distribution
Poisson Distribution
probability
Arrival per unit time(λ)

8. Service Pattern
Exponential Distribution
•Number of servers
and speed of service
to be considered.
•The time taken by
a server to service a
customer is known
as Service Time.
It is represented by
Exponential
Distribution
probability
Customer served
per unit time (μ)
Assumption:
λ<μ

9. Service Channels
• Single channel queuing system
• Multi channel queuing system
• Single channel multi phase system
• Multi channel multi phase system

10. Service Discipline
• FCFS (First-Come-First-Served)
• LCFS (Last-Come-First-Served)
• Service in random order
• Priority service

11. System Capacity
• Maximum number of customers that can be
accommodated in the queue.
• Assumed to be of infinite capacity.

12. Customer’s Behavior
• Balking- When a customer leaves the queue
because it is too long, has no time to wait, no
space to stand etc.
• Reneging- When a customer leaves the queue
because of his impatience.
• Jockeying- When a customer shifts from one
queue to another.

13. Service Facility Behavior
•Failure: A server may fail while
serving a customer, thereby
interrupting service untill a repair
can be made.
•Changing service rate: A server
may speed up or slow down,
depending on the number of
customers in the queue.
•Batch processing: A server may
service several customers
simultaneously.

14. Waiting and Idle time costs
Cost of waiting customers Cost of idle service facility
• Indirect cost of business loss
• Direct cost of idle equipment
or person.
• Payment to be made to the
servers(engaged at the
facilities),for the period for
which they remain idle.
The optimum balance of costs
can be made by scheduling
the flow of units or providing
proper number of service
facilities .

15. Totalexpectedcostof
operatingfacility
Increased service
Total expected cost
Cost of providing
service
Waiting time costs
Total expected cost = waiting time cost + cost
of providing service
Let Cw = expected waiting
cost/unit time
Ls= expected no. of units
Cf = cost of servicing one unit
Expected waiting cost= Cw. Ls
=Cw.[λ /(μ-λ )]
Expected service cost/unit time=
Cf.μ
Total cost , C = Cw. [λ/(μ-λ)] +μCf
This will be minimum if d/dμ(C)=0
Or if
-Cw.[λ/(μ-λ)²]+Cf=0 ,
Which gives ..
μ=λ±sqrt(Cw .λ/Cf)

16. Transient & Steady State of the
system
• When the operating characteristics are
dependent on time, it is said to be a transient
state.
• When the operating characteristics are
independent of time, it is said to be a steady
state.

17. Traffic intensity
The ratio λ/μ is called the traffic intensity or the
utilization factor and it determines the degree to
which the capacity of service station is utilized.

18. Applications of Queuing Model
• Telecommunications
• Traffic control
• Determining the sequence of computer
operations.
• Predicting computer performance
• Health services (e.g.. control of hospital bed
assignments)
• Airport traffic, airline ticket sales
• Layout of manufacturing systems.

19. Thank you