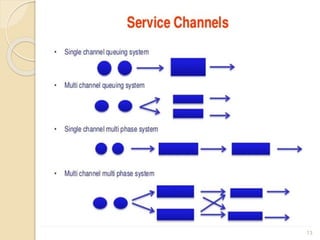
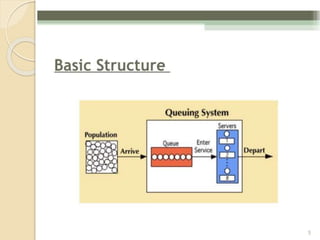
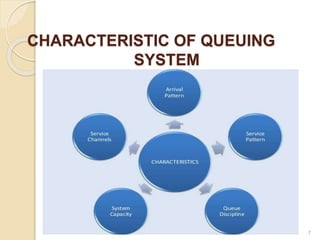
The document provides an overview of queueing theory, focusing on continuous parameter Markov chains, and outlines key elements such as customer behavior, service patterns, and various queue disciplines. It details the characteristics of queuing systems, applications in different fields, and introduces important terminologies and classifications of queues, including transient and steady states. Additionally, it discusses theoretical frameworks like Kendall's notation and the birth-death process in modeling queueing systems.

1. Queueing theory
Unit V
Continuous parameter
Markov chain
prepared
by
G.ABILAASHA,AP/Mathematics
SVCET
1

2. Introduction
 The first queueing
theory problem was
considered by Erlang in
1908 who looked at how
large a telephone
exchange needed to be
in order to keep to a
reasonable value the
number of telephone
calls not connected
because the exchange
was busy (lost calls).
2

3. Queueing theory is the
mathematical study of waiting
lines, or queues.
3

4. Key elements of queuing
systems• Customer
refers to anything that arrives at a facility
and requires service, e.g., people,
machines, trucks, emails.
• Server
refers to any resource that provides the
requested service, eg. repairpersons,
retrieval machines, runways at airport.
4

5. 5

6. CHARACTERISTIC OF
QUEUING SYSTEM
1. The Input or arrival-pattern
2. The Output or service-pattern
3. Queue Discipline
4. System Capacity
5. Service channels.
6

7. CHARACTERISTIC OF QUEUING
SYSTEM
7

8. The input(arrival pattern)
 The input describes the way in which
customers arrive and join the system.
 We deal with those queuing system in
which the customers arrive in poisson
fashion.
 The mean arrival rate is
 Interarrival time =1/ arrival rate

8

9. The output (Service Pattern)
 The time taken by a server to service a
customer is known as Service Time.
 Number of servers and speed of service to
be considered.
 It is represented by µ
9

10. The queue discipline
 It is a rule according to which customers are
selected for service when a queue has been
formed.
 The most common disciplines are
1. FCFS[ First Come First Serve]
2. FIFO[ First In First Out]
3. LIFS [ Last Come First Serve]
4. SIRO[ Service in random Order]
10

11. Service capacity
 Maximum number of customers
that can be accommodated in the
queue.
• Assumed to be of infinite capacity.
11

12. Service Channels
• Single channel queuing system
• Multi channel queuing system
• Single channel multi phase system
• Multi channel multi phase system
12

13. 13

14. Customer’s behavior
The customers generally behave in the
following four ways.
1. Balking
A customer who leaves the queue
because the queue is too long and he has no
time to wait or has no sufficient waiting
space.
2. Reneging
A waiting customer leaves the queue due
to impatience.
3. Jockeying
Customers may jockey from one waiting
line to another to their reasons.
4. Priority
Some customers are served before others
regardless of their order to arrival. 14

15. Applications of Queuing Model
 Telecommunications
• Traffic control
• Determining the sequence of
computer operations.
• Predicting computer performance
• Health services (e.g.. control of
hospital bed assignments)
• Airport traffic, airline ticket sales
• Layout of manufacturing systems.
15

16. BASIC POINTS
1. Customer(Arrival)
The arrival unit that requires some services to
performed.
2. Queue:
The number of Customer waiting to be served.
3. Arrival Rate
The rate which customer arrive to the service
station.
4. Service rate (µ)
The rate at which the service unit can provide
service to
the customer
5. Utilization Ratio Or Traffic intensity ( λ /µ )
λ / µ > 1 Queue is growing without end.
λ / µ < 1 Length of Queue is go on
diminishing.
λ /µ = 1 Queue length remain constant. 16

17. Transient & Steady State of the
system
• When the operating characteristics are
dependent on time, it is said to be a
transient state.
• When the operating characteristics are
independent of time, it is said to be a
steady state.
17

18. Kendall’s Notation
 Queues can be written in the form of
(a/b/c):(d/e)
Where a - Inter-arrival time distribution
b - Service time distribution
c - Number of servers
d - Maximum number of jobs that can
be
there in the system (waiting and in
service)
(Default ∞ for infinite number of waiting
18

19. Symbols for a and b
 M – Markovian(Poisson arrival) or
departure distribution(or exponential
inter arrival or service time
distribution)
 Ek – Erlangian or Gamma inter arrival
or service time
 GI – General independent arrival
distribution
 G – General departure distribution
 D – determine inter arrival or service
time 19

20. Four important queueing
systems
1. (M/M/1) : (∞/FIFo)
2. (M/M/s) : (∞/FIFo)
3. (M/M/1) : (k/FIFo)
4. (M/M/s) : (k/FIFo)
20

21. 21

22.  Pure Birth Process
The arrival process assumes that the
customers arrive at the queueing
system and never leave the system is
called Pure Birth Process
 Pure Death Process
The departure process assumes that
no customer joins the system while
the service is continued for those who
are already in the system
22

23.  Birth and Death process
The simultaneous occurrence of arrivals
and departure is called Birth and Death
process
1. (M/M/1) : (∞/FIFo)
2. (M/M/s) : (∞/FIFo)
3. (M/M/1) : (k/FIFo)
4. (M/M/s) : (k/FIFo)
23

24. TERMINOLOGY
  - the mean arrival rate
  - the mean service rate
 Pn- the probability of n customers
in the system
 P0 - the probability of an idle
system
  - the traffic intensity /utilisation
period/busy period
24

25. TERMINOLOGY
Continues…
 Ls - the average number of
customers in the system,
 Lq - the average number of
customers in the queue.
 Ws - the average waiting time per
customer.
 Wq - the average time a customer is
in the queue.
25

26. 1. (M/M/1) : (∞/FIFo)
1.  =
2. P0 = 1  
3. Pn = P0n
Little’s Formula
Ls = Ws = Ls
Lq = Ls - Wq = Lq


1





1

1
26

27. Thank You
27