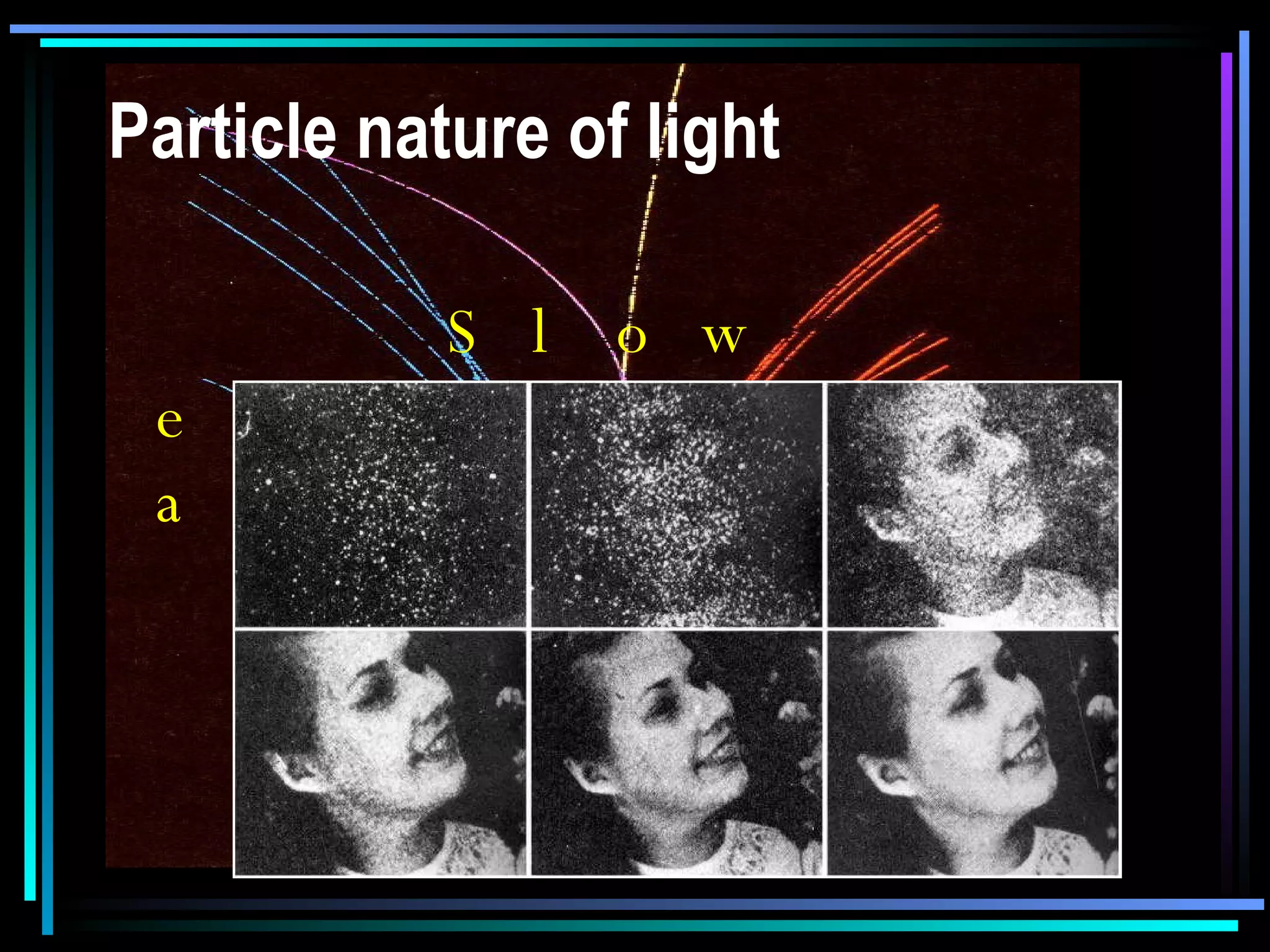
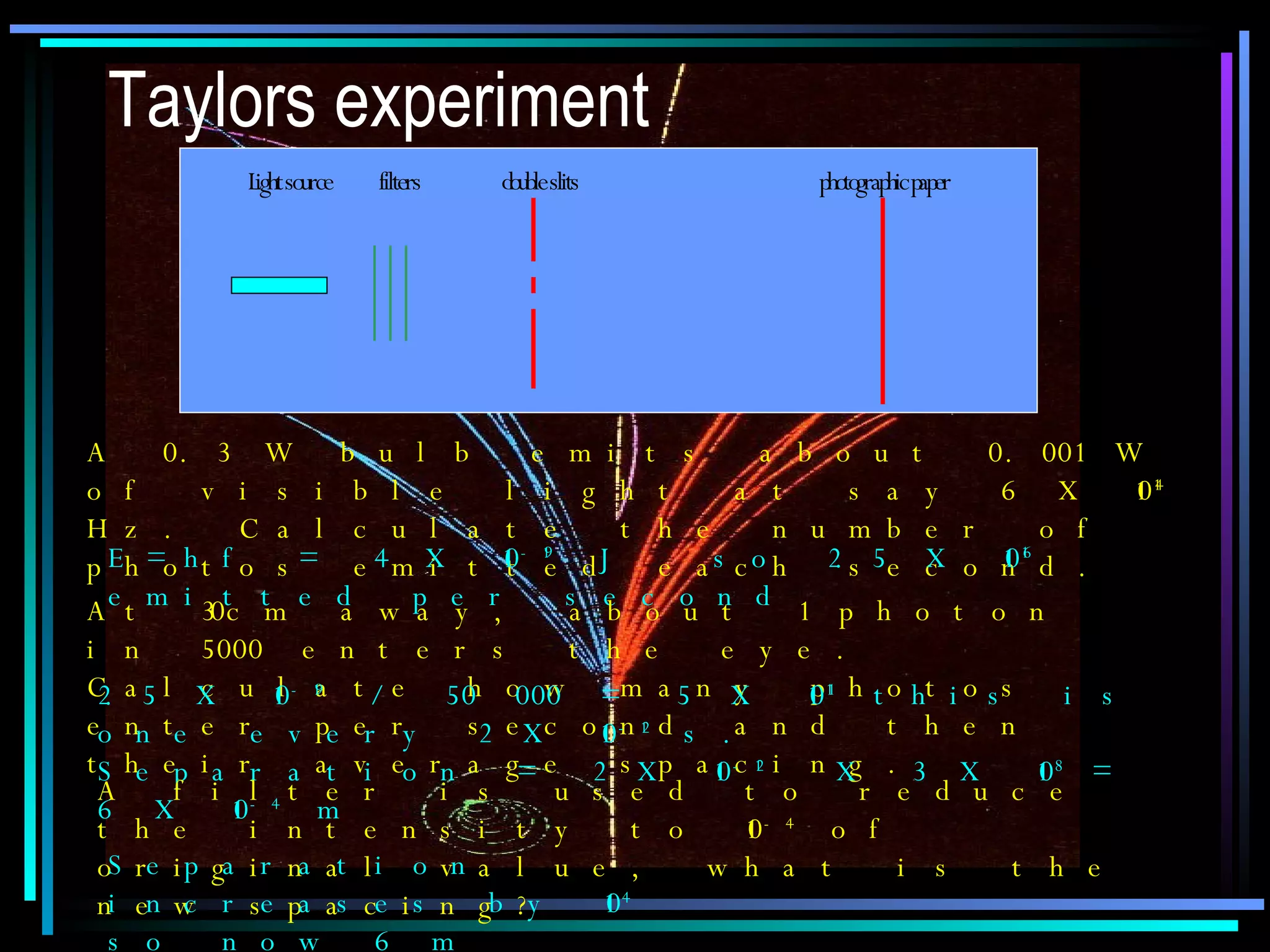
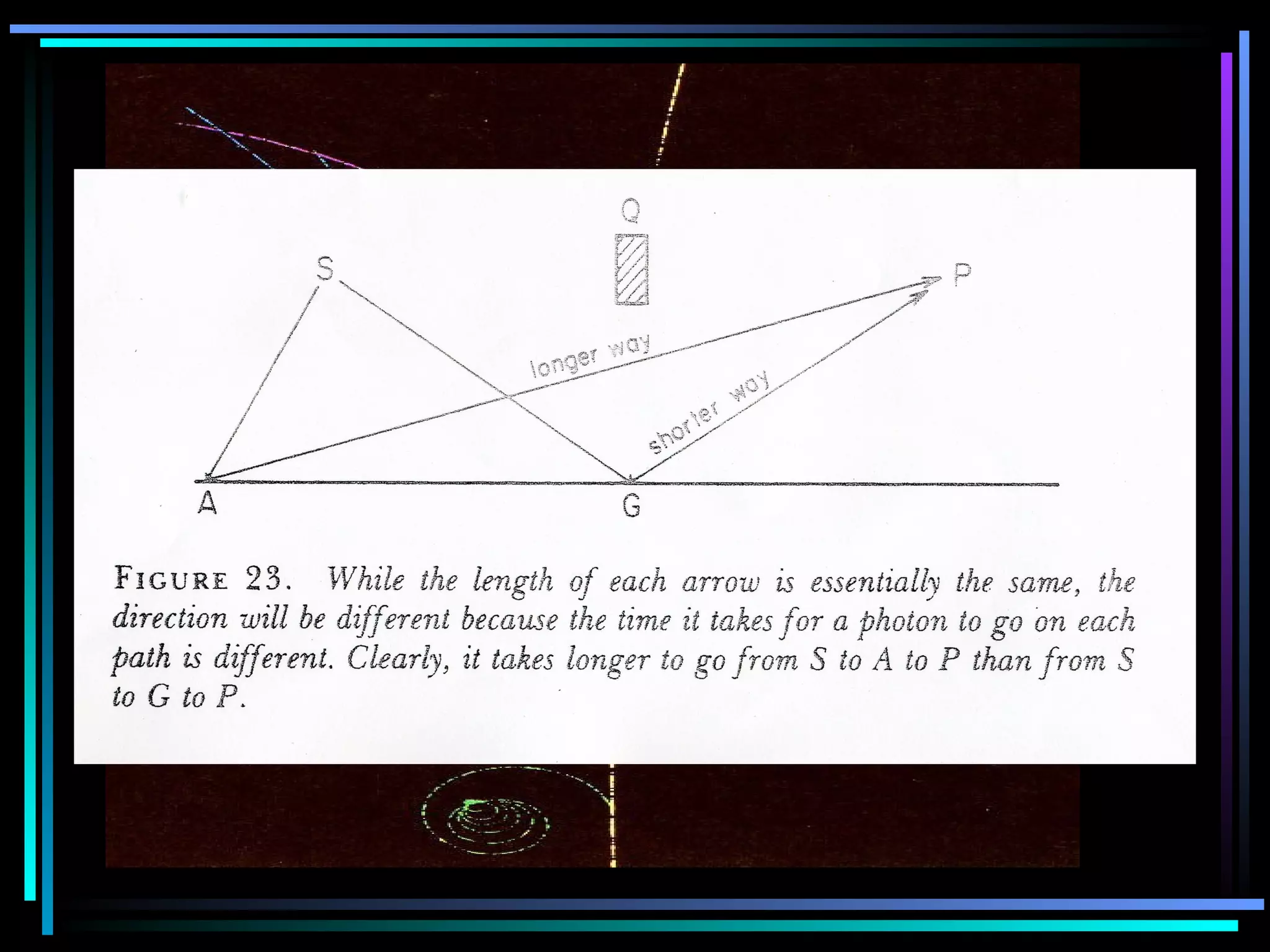
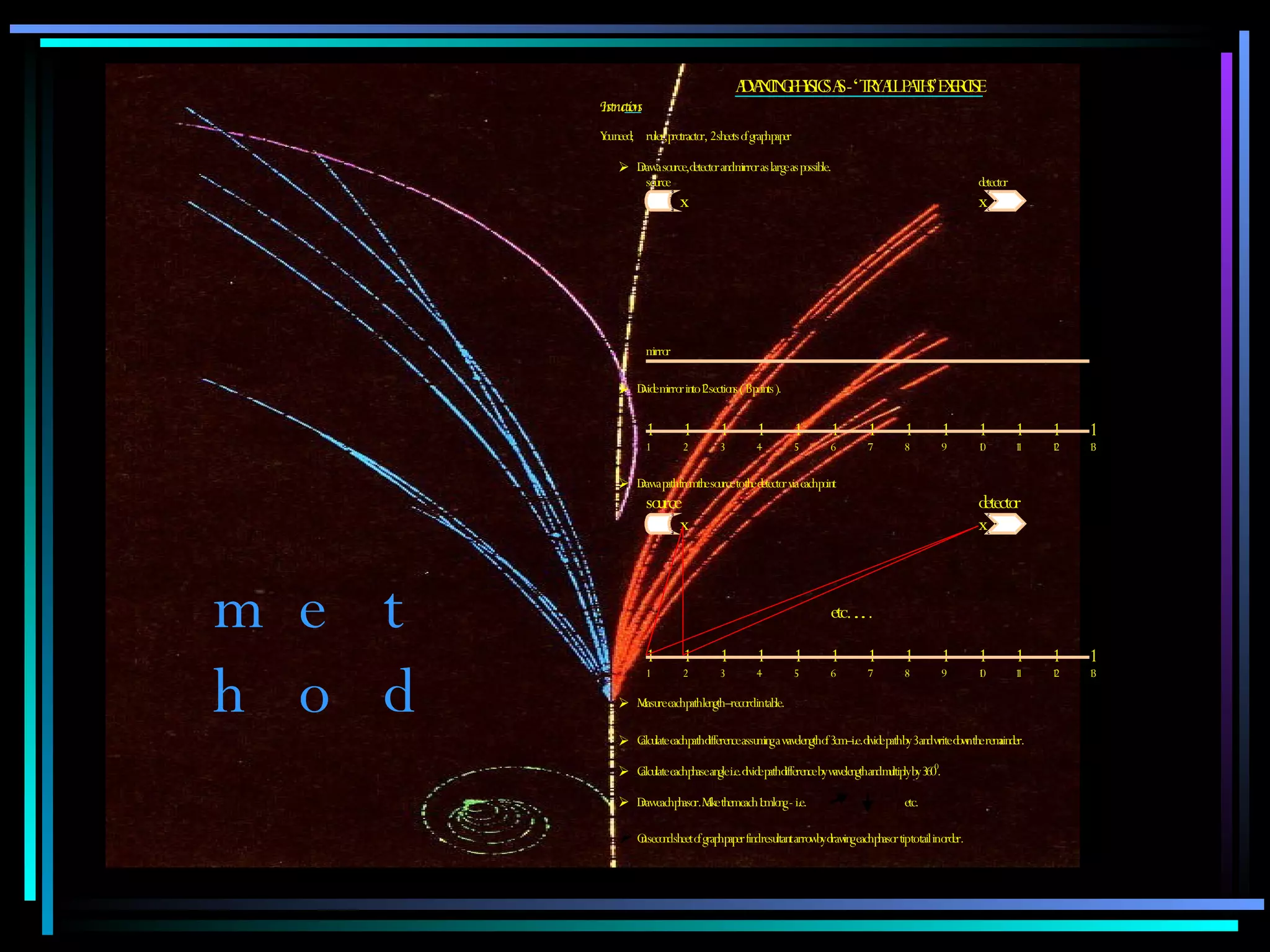
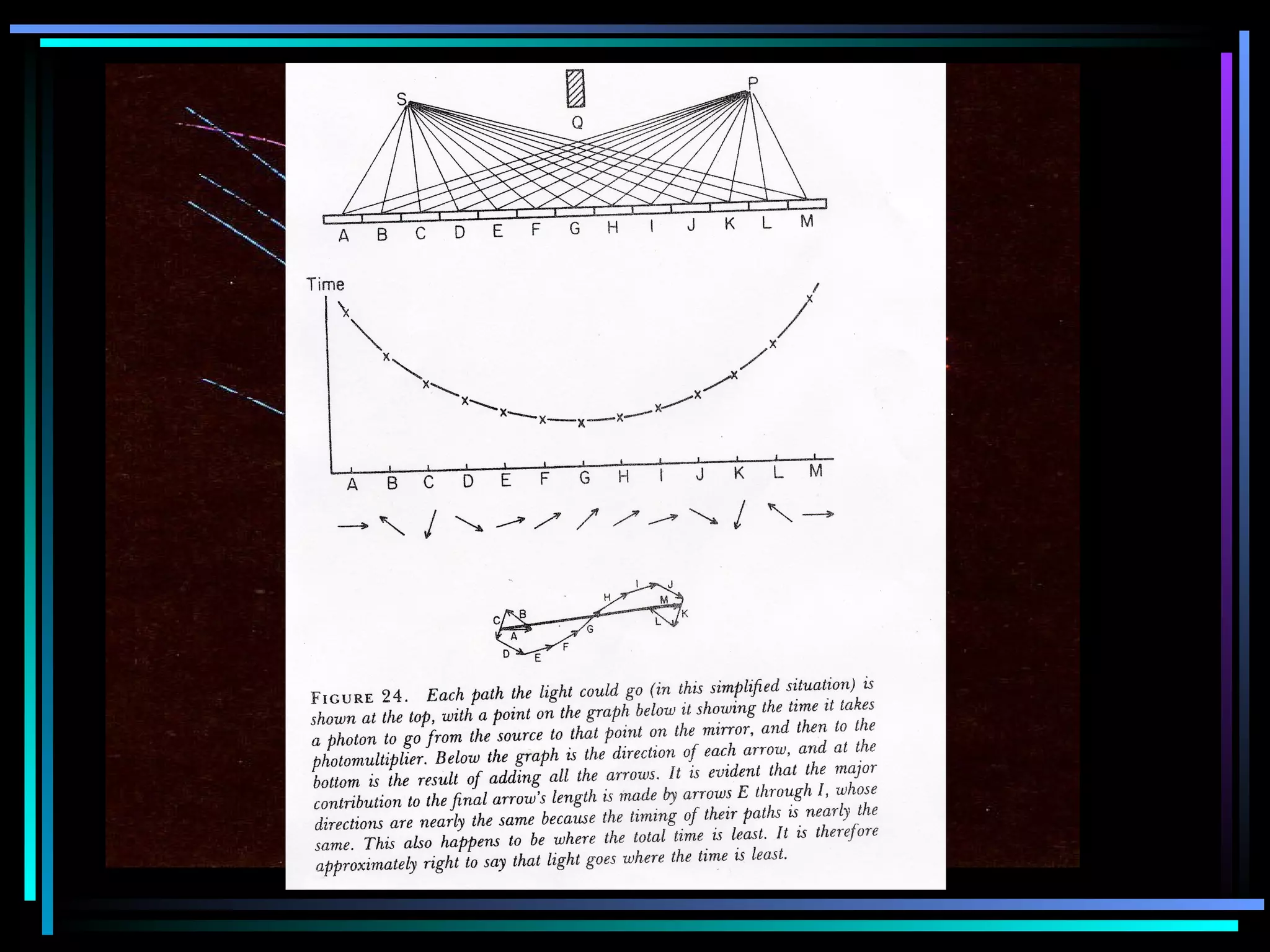
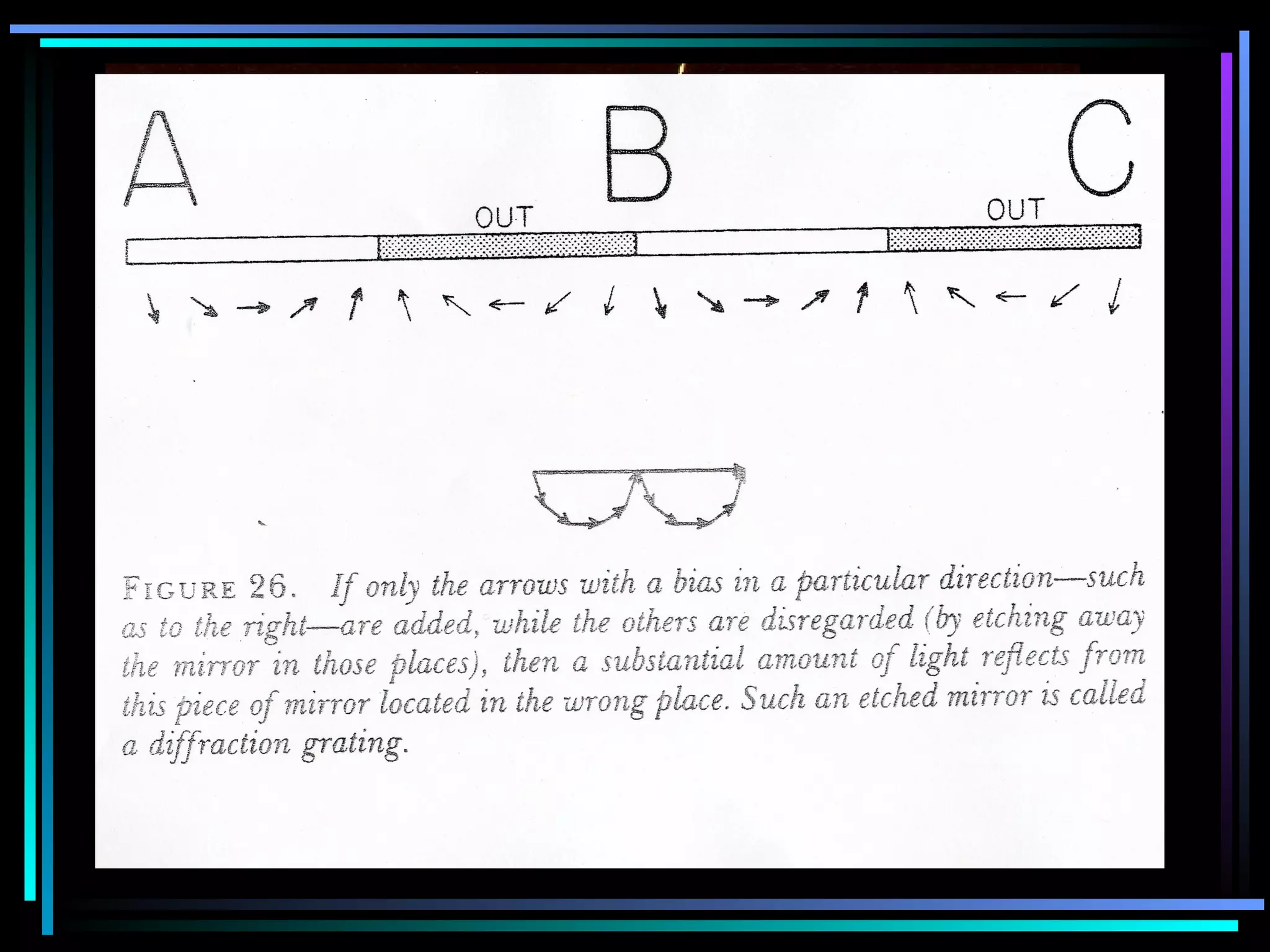
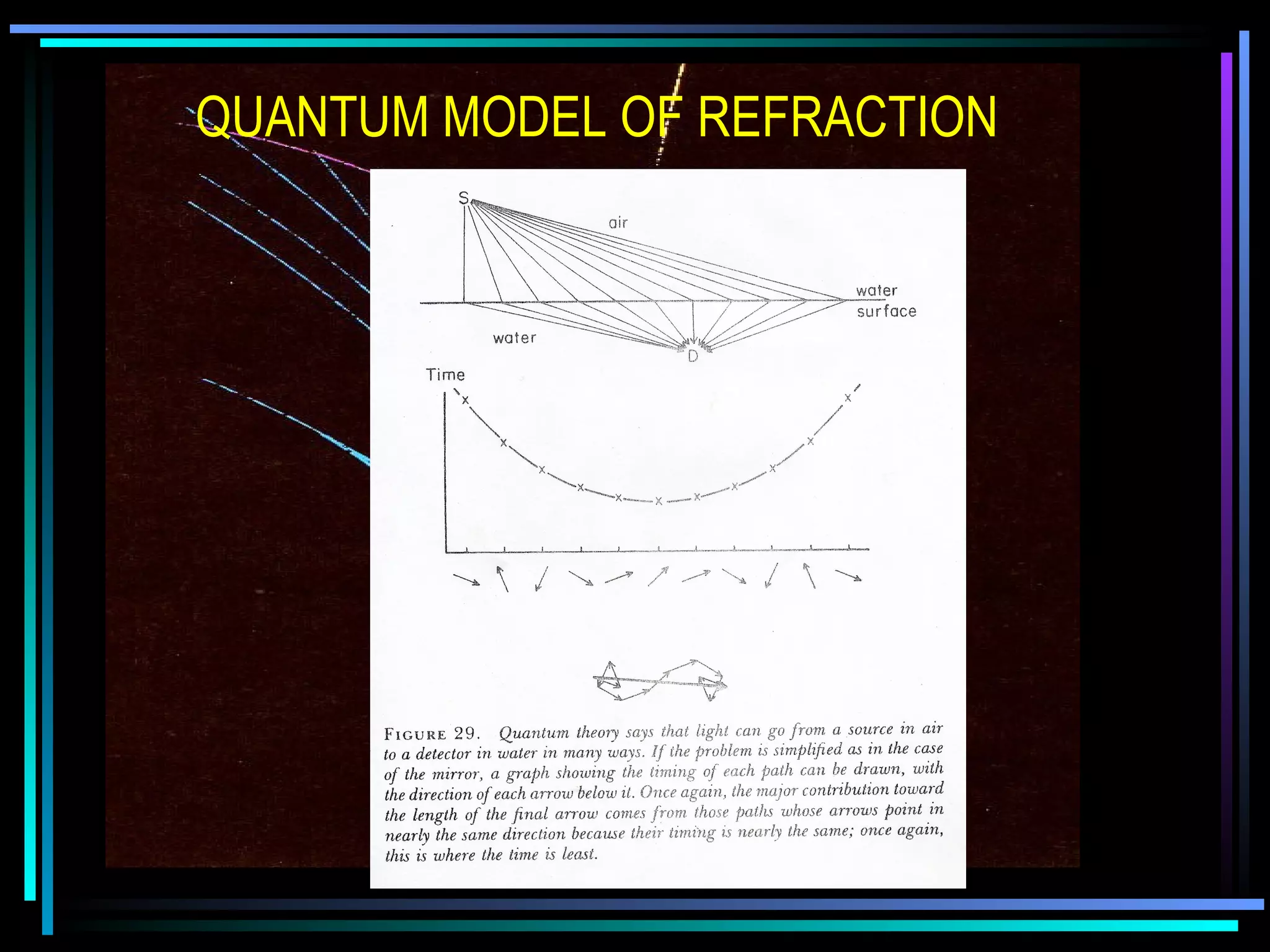
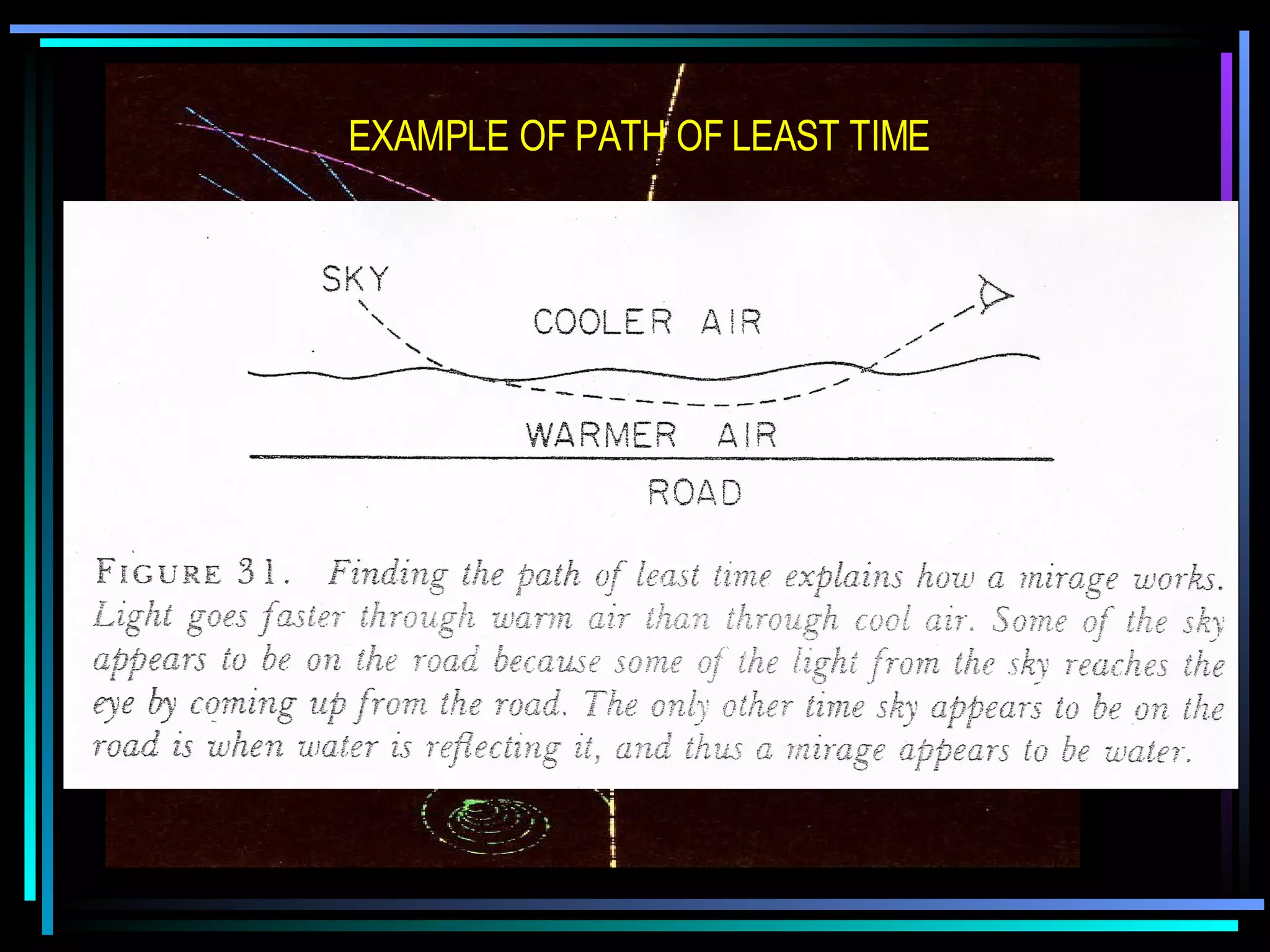
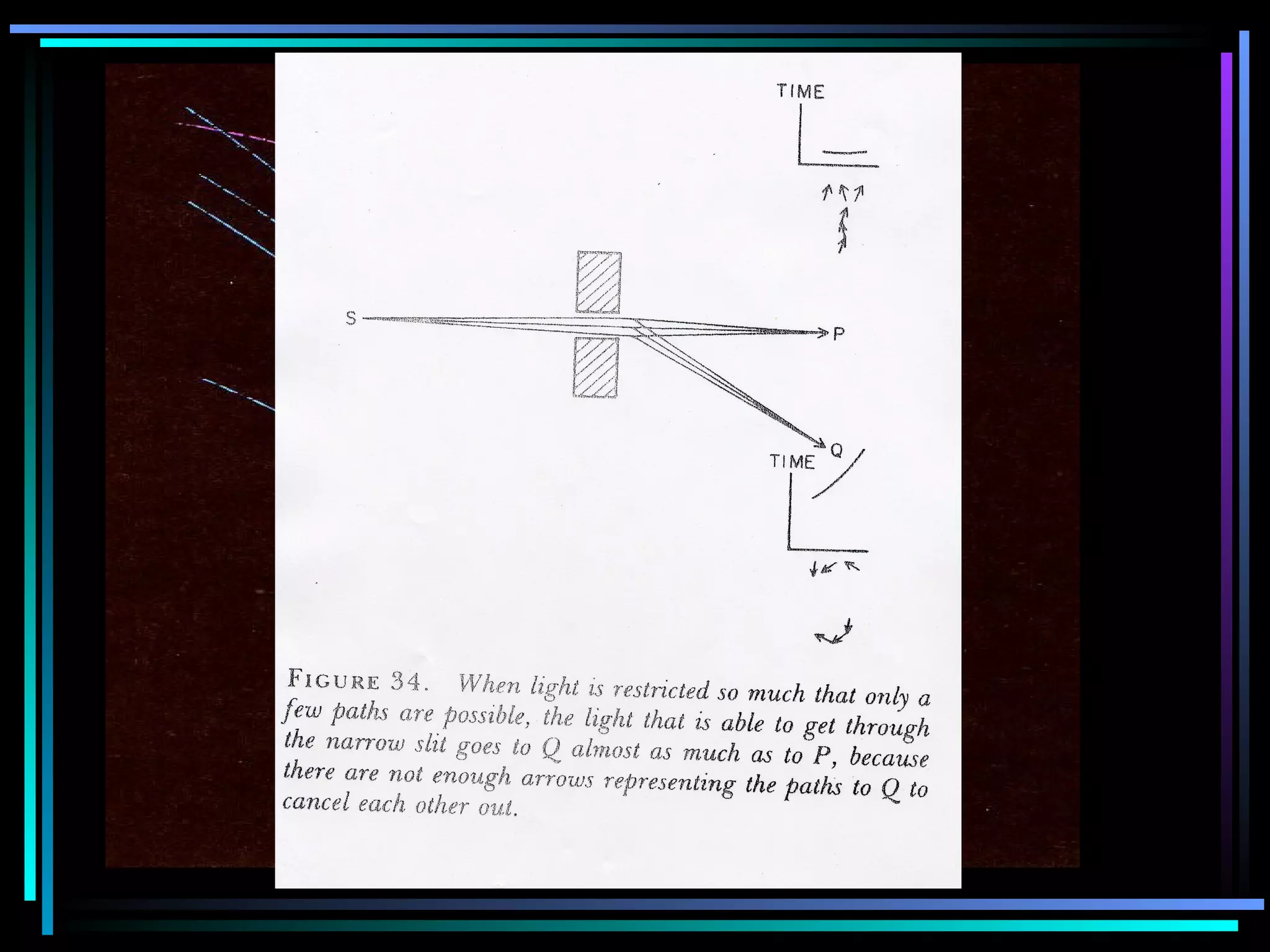
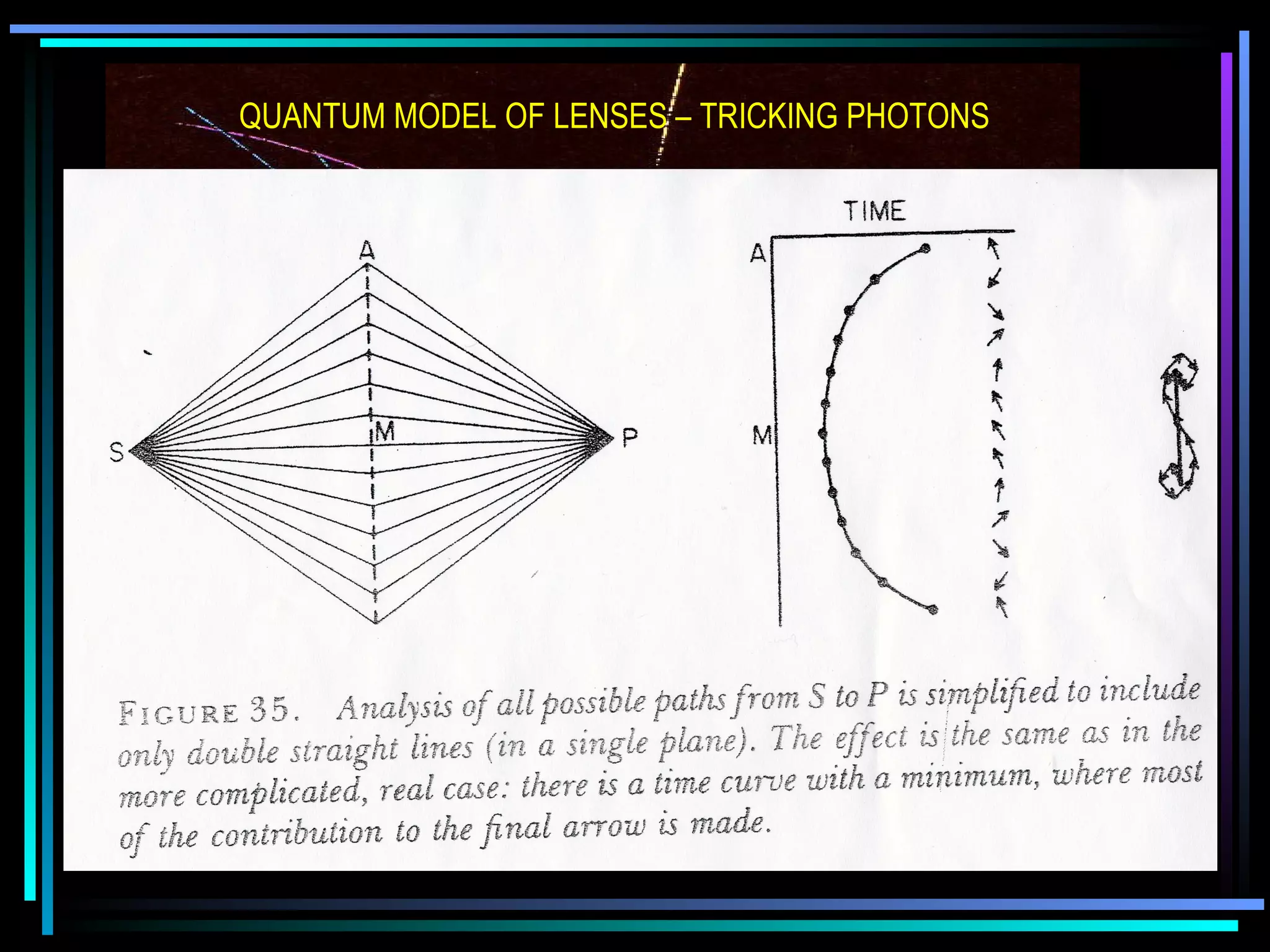
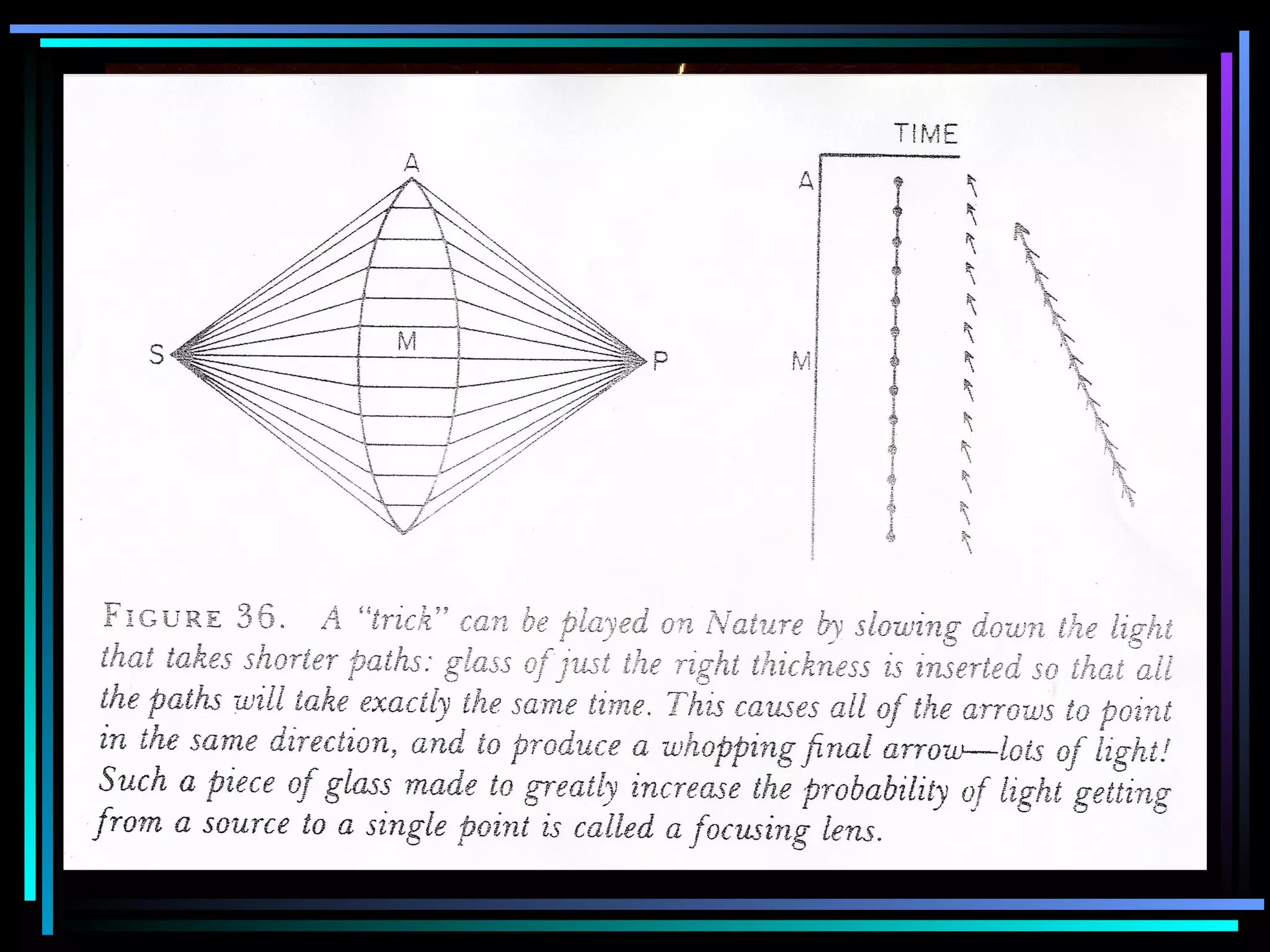
This document provides an introduction to quantum theory through a two-lesson presentation. It discusses the wave and particle nature of light through experiments demonstrating diffraction and photon counting. It introduces Richard Feynman and explains that photons have energy proportional to their frequency and travel in probabilistic paths. The document uses diagrams and exercises to illustrate how the quantum model accounts for reflection, refraction, diffraction, and interference through graphical addition of phasors representing phase and amplitude along different possible photon paths.

1. quantum theory NJF

2. Introduction This is a two lesson presentation. It is designed to help you understand the true weirdness of nature, i.e.quantum theory. Don’t get too comfy – you are going to do some work. Concentrate and ask questions.

3. Wave nature of light This image is of a bright light photographed through 'crossed gratings' – two diffraction gratings set perpendicular to one another.

4. Particle nature of light Slow exposure of a photograph

5. Taylors experiment A 0.3 W bulb emits about 0.001 W of visible light at say 6 X 10 14 Hz. Calculate the number of photos emitted each second. E=hf = 4 X 10 -19 J so 2.5 X 10 16 emitted per second At 30cm away, about 1 photon in 5000 enters the eye. Calculate how many photos enter per second and then their average spacing. 2.5 X 10 -19 / 50 000 = 5 X 10 11 this is one every 2 X 10 -12 s. Separation = 2 X 10 -12 X 3 X 10 8 = 6 X 10 -4 m A filter is used to reduce the intensity to 10 -4 of original value, what is the new spacing? Separation increases by 10 4 so now 6 m

6. “ It does not do harm to the mystery to know a little about it. Far more marvellous is the truth than any artists of the past imagined! ” - Richard Feynman It takes a little genius

7. Who was Richard Feynman? “ Richard Feynman was to the second half of the 20 th century what Einstein was to the first: the perfect example of scientific genius” Frank McLynn, Independent.

8. A new way of seeing

9. The truth about light It comes in packets called photons. They each have an energy E=hf Dim blue light contains identical photons to bright blue light – just less of them. We can never know the route a photon will take we can only calculate probabilities. QUANTUM THEORY RECONCILES THESE FACTS WITH THE OBSERVED WAVE LIKE BEHAVIOUR OF LIGHT e.g. INTERFERENCE, DIFFRACTION ….

10. Real reflection

11. Introduction All paths method – look at text book page 163

12. QUANTUM MODEL OF REFLECTION

14. Ask: In what ways can we…? Assess the situation. Get the facts. Generate possible solutions with green light, non-judgmental thinking. Select the best solution.

15. Results table EXERCISE 1

16. method

18. Adding arrows. Finding probability.

19. TESTING THE THEORY

21. QUANTUM MODEL OF REFRACTION

22. EXERCISE 2 Homework ‘ try all paths refraction’

23. EXAMPLE OF PATH OF LEAST TIME

24. QUANTUM MODEL OF DIFFRACTION

26. QUANTUM MODEL OF LENSES – TRICKING PHOTONS

28. SUMMARY Photons show quantum behaviour. Quantum behaviour is unique – neither wave nor particle behaviour. Quantum behaviour combines phasors from all possible paths. The probability of an event is got from the square of the resultant phasor amplitude.

29. I can show my understanding of effects, ideas and relationships by describing and explaining: how phasor arrows come to line up for paths near the path that takes the least time how phasor arrows 'lining up' and 'curling up' accounts for reflection, propagation, refraction, focusing, diffraction and interference that the probability of arrival of a photon is determined by graphical addition of arrows representing the phase and the amplitude of the quantum for selected possible paths evidence for random arrival of photons I can interpret: diagrams illustrating how paths contribute to an amplitude LEARNING OUTCOMES

30. Recommended Reading QED the strange theory of light and matter. Six Easy Pieces