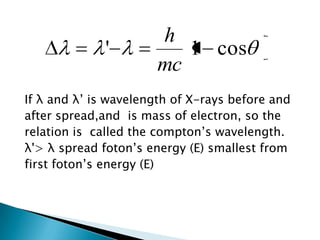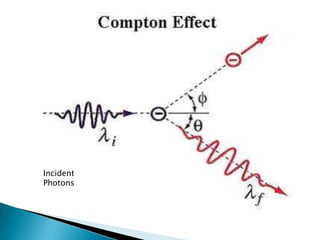
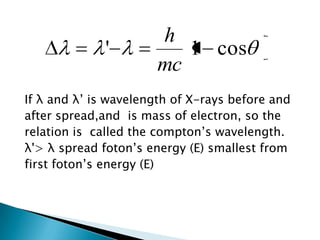
The document discusses the dual wave-particle nature of light and photons. It explains that light exhibits both wave features like frequency and wavelength, as well as particle features like energy and momentum. The document also discusses Compton scattering, where photons transfer some of their energy to electrons, increasing their wavelength. Additionally, it covers de Broglie's proposal that matter has both wave and particle properties, and introduces the concept of de Broglie wavelength for particles like electrons.

1. LIGHT DUALISM

2. The dual wave-particle nature of light is nowa basic part of the theory of light.Wave feature: υ, λ;Particle feature: E, p;Photonsenergy: E=hυ;momentum: p=h/λ, k=2/λWave-particle duality of light

3. Incident Photons

4. If λ and λ’ is wavelength of X-rays before andafter spread,and is mass of electron, so the relation is called the compton’swavelength.λ'> λ spread foton’s energy (E) smallest fromfirst foton’s energy (E)

5. In1924, Louis de Broglie proposed that matter possesses wave as well as particle characteristics, receiving the Nobel Prize in 1929.A moving body behaves in certain ways as though it has a wave nature.Photon wavelength: De Broglie wavelengthDe Broglie

6. ExerciseWrite down the formula for a. Energy Photon after scattered in effect Compton b. De Broglie Wavelength 2. Calculate the momentum for electrons has wavelength 3. Find the change in wavelength of an X-ray photon when it is scattered through an angle4. If the de Broglie wavelength of an electron is equal to , calculate it’s energy kinetic