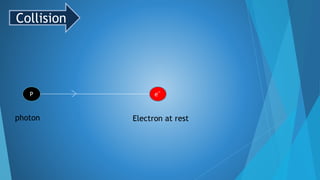
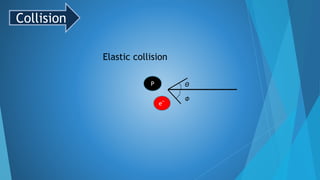
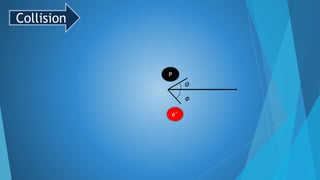
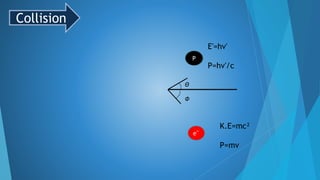
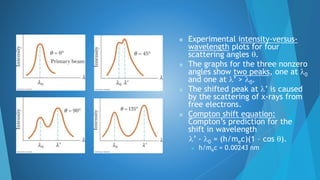
This document summarizes Compton scattering and Compton's experiment that provided evidence for Einstein's photon concept. It introduces Compton scattering as the inelastic scattering of photons from electrons, which results in a wavelength shift (Compton shift) according to the Compton shift equation. The theory section derives equations for the kinetic energy of the recoiled electron and the scattering angle based on conservation of energy and momentum. Key results are presented, including that the maximum kinetic energy is achieved for backscattering at 180 degrees. The document concludes by describing Compton's experimental results, which showed intensity peaks at both the initial and shifted wavelengths, confirming Compton scattering.

1.  REPRESENTED BY
ABDUL SALIM
Govt. Engineering College,
Ajmer
B.Tech(Computer Science)
1st year(2nd semester)
Compton Effect

2.  Introduction
 Theory
 Compton Shift
 Direction of recoil electron
 Kinetic energy of recoil electron
 Experimental demonstration

3. Introduction
In 1923, Compton’s Experiment Of X-ray
Scattering From Electrons Provided The
Direct Experimental Proof For Einstein’s
Concept Of Photons.
Einstein’s Concept Of Photons
Photon Energy: E = hv
Photon Momentum P: = E/c = hv/c=h/.
Compton’s Apparatus To Study
Scattering Of X-rays From Electrons
A.H. Compton

4. THEORY
for elastic collision
Total energy of the = Total energy after
system before collision collision
hv+m₀c²=hv´+mc²
 according to compton
 electron scattered by photon
 collision is elastic
 e gains some kinetic energy & recoil at angle Ф
 photon is recoil at angle θ

5. e‾P
Collision
Electron at restphoton

6. e‾P
Collision

7. e‾P
Collision
Elastic collision
e‾ gain kinetic energy

8. e‾
P
Collision
Elastic collision
Θ
Ф

9. e‾
P
Collision
Θ
Ф

10. e‾
P
Collision
Θ
Ф
E′=hv′
P=hv′/c
K.E=mc²
P=mv

11. Derivation
For elastic collision
According to momentum conservation along the direction of incident photon;
hv/c + 0 = hv´cosθ/c + mvcosΦ
Perpendicular to the direction of incident photon;
0 = hv´sinθ/c - mvsinΦ
h(v - v´) + m₀c² = mc²
m = ___m₀____
√1-v²/c²
    cos12
 hhhhcme

12. Continuing on
And using v=c/λ we arrive at the Compton effect
And h/mc is called the Compton wavelength
)cos1(2






cm
h
e
  cos1
cm
h
e
m
cm
h
e
C
12
1043.2 


13. Summarizing and adding a few other useful results are
 
 























2
tan1cot
cos11
cos1
2
2






cm
hv
hhT
cm
hv
hv
h
cm
h
e
e
e
e
Total kinetic energy

14. Kinetic Energy of Recoil Electron
According to energy conservation law
K.E = hv - hv´ = hv(1 - v´/v)
v´ 1
V 1 + α(1 – cosθ)
2hvαsin²θ/2
1 + 2αsin²θ/2
K.E =
α = hv/m₀c²
When θ = π(Back scattering)
(K.E)max = 2αhv/(1+2α)
When θ = π/2
K.E = hvα/(1+α)
When θ = 0 (No scattering)
K.E = 0

15. Direction of recoil electron
mvcsinΦ hv´sinθ
mvccosΦ hv - hv´cosθ
= =tanΦ
sinθ
v/v´ - cosθ
tanΦ = = sinθ
(1+α)(1 – cosθ)
cotθ/2
1 + hv/m₀c²
tanΦ =

16. Special case
When θ=0
cos 0 =1
∆λ=λ˛(1 - cos θ) = 0
When θ=π/2
cos π/2 = 0
∆λ=λ˛(1 - cos θ) = λ˛
When θ=π
cosπ= -1
∆λ=λ˛(1 - cos θ) =2λ˛
No scattering
Scattering
perpendicular
Back scattering

17. Results of Compton’s scattering experiment

18.  Experimental intensity-versus-
wavelength plots for four
scattering angles .
 The graphs for the three nonzero
angles show two peaks, one at 0
and one at ’ > 0.
 The shifted peak at ’ is caused
by the scattering of x-rays from
free electrons.
 Compton shift equation:
Compton’s prediction for the
shift in wavelength
’ - 0 = (h/mec)(1 – cos ).
 h/mec = 0.00243 nm

19. Thank You