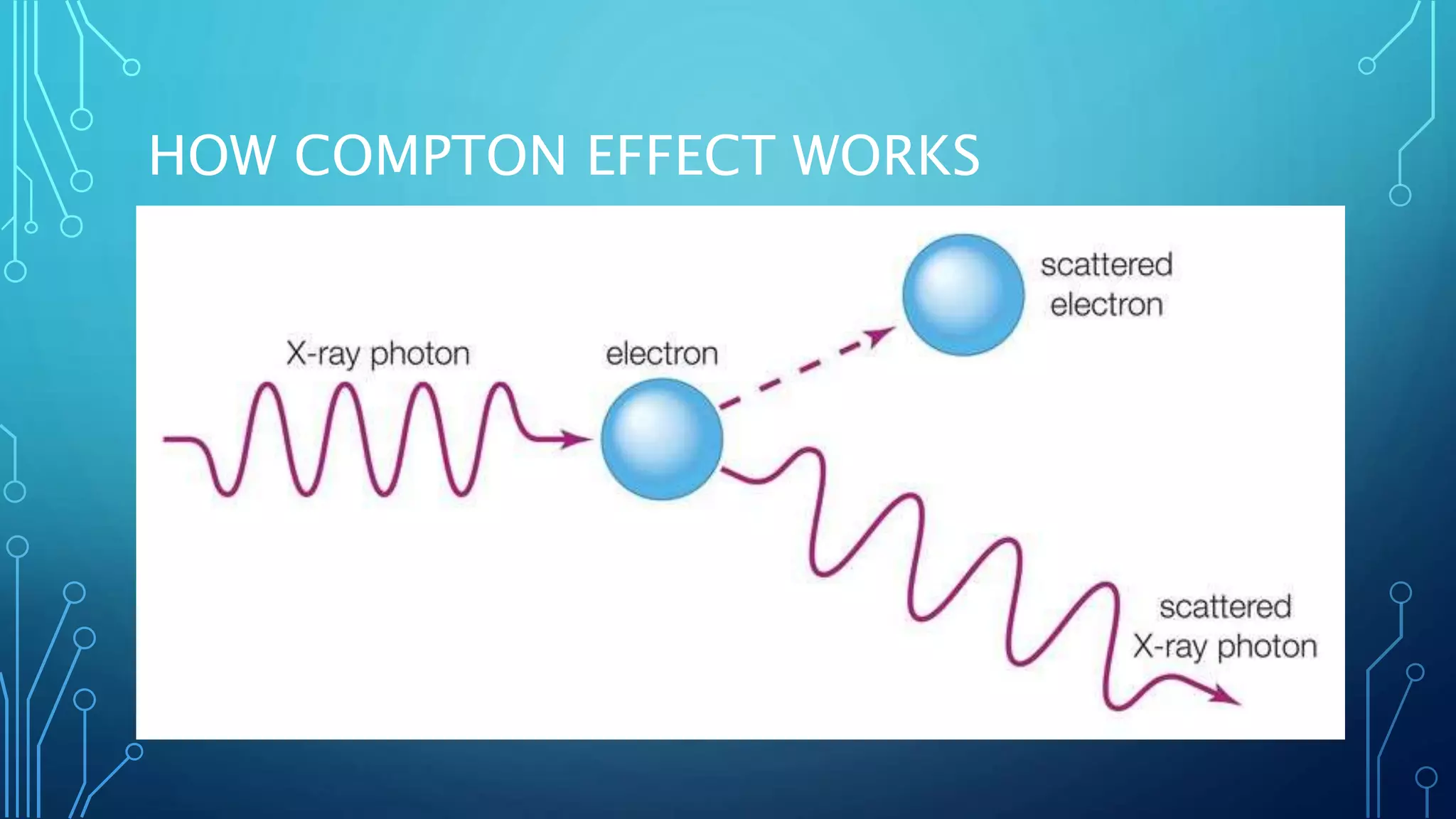
The Compton effect occurs when a high-energy photon collides with an electron, causing the photon to lose some energy and increase in wavelength. Arthur Holly Compton discovered this effect in 1923 through experiments bombarding a graphite target with x-rays and measuring the wavelength of scattered radiation. The effect showed that light behaves as both a particle and wave and is important in fields like radiation therapy and gamma spectroscopy. It is explained by the transfer of momentum and energy between the photon and electron during collision.

1. THE COMPTON EFFECT

2. MD. OBAIDULLAH AL-FARUK
ID: 2013-2-60-038
MD MAMUN HOSSAIN
ID: 2015-2-60-016
A.S.F. RABBY PATHAN
ID: 2014-2-60-074

3. FIRST INTRODUCED
The Compton effect was first demonstrated in 1923 by Arthur
Holly Compton (for which he received a 1927 Nobel Prize in
Physics)
Compton's graduate student, Y.H. Woo, later verified the effect.

4. DEFINITION
• The Compton effect (also called Compton scattering) is the result of a
high-energy photon colliding with a target, which releases loosely
bound electrons from the outer shell of the atom or molecule .
• The scattered radiation experiences a wavelength shift that cannot be
explained in terms of classical wave theory, thus lending support to
Einstein's photon theory.
• Probably the most important implication of the effect is that it
showed light could not be fully explained according to wave
phenomena.

5. APPLICATIONS
• Compton scattering is of prime importance to radiobiology, as it
happens to be the most probable interaction of high energy X rays
with atomic nuclei in living beings and is applied in radiation therapy.
• In material physics, Compton scattering can be used to probe the
wave function of the electrons in matter in the momentum
representation.
• Compton scattering is an important effect in gamma spectroscopy
which gives rise to the Compton edge, as it is possible for the
gamma rays to scatter out of the detectors used. Compton
suppression is used to detect stray scatter gamma rays to counteract
this effect.

6. THE EXPERIMENT A graphite target was
bombarded with monochromatic
x-rays and the wavelength of the
scattered radiation was
measured with a rotating crystal
spectrometer. The intensity was
determined by a movable
ionization chamber that
generated a current proportional
to the x-ray intensity. Compton
measured the dependence of
scattered x-ray intensity on
wavelength at three different
scattering angles of 45o 90o ,and
135o

7. The Experimental
intensity vs wavelength
plots observed by
Compton for the three
scattering angles show
two peaks , one at the
wavelength λ of the
incident X-rays and the
other at a longer
wavelength λ’ .
λ
λ
λ'
λ'
λ'
λ'
λ'

8. HOW COMPTON EFFECT WORKS

9. • The incident photon has the following energy E and linear momentum p:
E = hc / lambda
p = E / c
Analyzing these energy and momentum relationships for the photon and
electron , end up with three equations:
• energy
• x-component momentum
• y-component momentum
... in four variables:
• phi, the scattering angle of the electron
• theta, the scattering angle of the photon
• Ee, the final energy of the electron
• E', the final energy of the photon

10. • If we care only about the energy and direction of the photon,
then the electron variables can be treated as constants,
meaning that it's possible to solve the system of equations. By
combining these equations and using some algebraic tricks to
eliminate variables, Compton arrived at the following equations
:
1 / E' - 1 / E = 1/(me c2) * (1 - cos theta)
lambda' - lambda = h/(me c) * (1 - cos theta)
• The value h/(me c) is called the Compton wavelength of the
electron and has a value of 0.002426 nm (or 2.426 x 10-12 m).
This isn't, of course, an actual wavelength, but really a