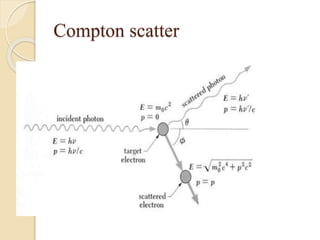
The document discusses the Compton effect, where X-rays scatter off electrons. When X-rays interact with electrons at rest, the scattered X-rays exhibit lower frequencies than the incoming radiation. This was studied by Arthur Compton in 1926 and provided evidence for the photon theory of light. The document presents the assumptions of the Compton effect and a figure showing the interaction. It then derives the Compton scattering equation using conservation of energy and momentum, showing that the wavelength of the scattered photon increases relative to the incoming wavelength based on scattering angle.

1. The compton effect
Presented by: Sehrish Inam, Lecturer Physics

2. Table of contents
 Introduction
 Figure
 Discussion
 Equation

3. Compton scatter
 When X-rays are scattered due to interaction with
a light body such as an electron, the scattered rays
exhibit lower frequencies than the incident
radiation.
 Arthur Compton studied this phenomenon in
1926.
 It provides a solid support for photon theory of
light.

4. Compton scatter
 Assumptions
1. Energy of incoming photon, E = h𝜈
2. Electron to be targeted is considered at
rest.

5. Compton scatter

6. Compton scatter
 Figure shows interaction of photon and
electron and their scatter.
 Electron is treated at rest.
 Photon interacts with electron with
frequency 𝜈 and is scattered at an angle θ
with a lower frequency 𝜈’ .
 The photon energies before and after
collision are h𝜈and h𝜈’
 Momentum before and after collision are
h 𝑐
λ
and
h 𝑐
λ′
respectively.

7. Compton scatter
 Energy and momentum of the recoiled
electron E and P respectively.
 To get equation for compton scatter
wavelength we apply law conservation of
energy and momentum.
 Conservation of momentum along the line
of impact:

h𝜈
𝑐
= h𝜈′
𝑐
Cosθ+ pCosϕ --------------------(1)
 0 = h𝜈′
𝑐
Sinθ - pSinϕ -----------------------(2)

8. Compton scatter
 Conservation of energy before and after
collision:
h𝜈 + moc = h𝜈’ + E -------------------------(3)
1
𝜈′
- 1
𝜈 = h
𝑚𝑜𝐶2
( 1 − Cosθ )--------------------(4)
Using relation 𝜈 = c/λ equ 4 reduces to
λ’-λ = h
𝑚𝑜𝐶
( 1 − Cosθ ) ----------------------(5)
 Equation 5,gives the measure of increase in
wavelength of scattered photon.

9. Compton scatter
 The quantity
h
𝑚𝑜𝐶
in compton equation
is called compton wavelength.
 λc =
h
𝑚𝑜𝐶
= 2.426exp-12m