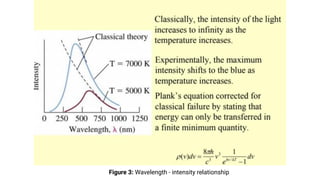
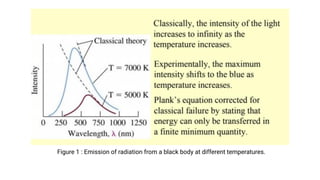
The document provides an introduction to quantum mechanics and its relevance in chemistry, covering topics such as black body radiation, the photoelectric effect, Planck's radiation law, and the Compton effect. It explains how classical mechanics differs from quantum mechanics, emphasizing the need for quantum theories to explain phenomena that classical theories cannot. Key concepts are illustrated with equations and examples, highlighting the particle nature of light and energy quantization.

1. Introduction Quantum Mechanics
(Chemistry)
By :Shriya Tiwari

2. Introduction Quantum Mechanics
(Chemistry)

3. Introduction
Quantum
Mechanics
(Chemistry)
1) Introductory to quantum chemistry
2) Black body radiation
3) Photoelectric effect
4) Plank’s radiation law
5) Compton effect

4. Introductory to Quantum Chemistry
Classical Mechanics
● Everyday sized objects
● Large
● Heavy
● Continuous
● Newton's law
● Trajectory
● Deterministic
● Intuitive
Quantum Mechanics
● Very, very small objects
● Small
● Light
● Discreet/quantized
● Schrondinger equation
● Wave function
● Probabilistic
● Non-intuitive

5. Black Body Radiation

6. ● Black Body
Radiation
Limitations of Electromagnetic Wave Theory
Electromagnetic wave theory explains the
properties of light such as interference and
diffraction etc. But this theory could not explain the
following facts :
● The phenomenon of black body radiation
● The photoelectric effect
These phenomenon could be explained only if
electromagnetic wave have particle nature.

7. ● Black Body
Radiation
Definition : An ideal black body is a perfect
absorber and perfect emitter of radiations. Such a
black body emits and absorbs radiations of all
frequencies which fall on its surface.
● The energy density, i.e, the amount of energy
radiated per unit volume by a black body
depends upon the temperature. However, the
energy radiated at a particular temperature is
not of a single frequency.
● The correlation between energy density and
wave length at different temperatures is
given in the fig. 1.The curves have following
characteristics.:-

8. Figure 1 : Emission of radiation from a black body at different temperatures.

9. ● Black Body
Radiation
● For each temperature, there is a particular
wavelength at which enery radiated is
maximum.
● The position of maximum shifts towards
lower wavelengths with increase in
temperature.
The curves referred to as black body
radiation curves. Thus, of all bodies heated
to a given temperature, maximum enery is
radiated by a black body.
These facts could not be explained by
classical wave theory.

10. Photoelectric Effect

11. ● Photoelectric
effect
Definition: photoelectric effect is the phenomenon
of ejection of electrons from the metal surface
when light of suitable frequency strikes the metal.
Electrons ejected are called photo-electrons.
Some important facts about photoelectric effect
1. For each metal, light of certain minimum
frequency is required to eject the electrons. It
is called threshold frequency (v0
) . It is
different for different metals. If the frequency
of light is less then that of threshold
frequency, no electrons are emitted no matter
how large the intensity is or how long the
light falls on the metal surface.
2. The kinetic enery of the emitted electrons is
directly proportional to the frequency of
incident radiation but is independent of its
intensity.

12. Figure 2: Explanation of photoelectric effect

13. ● Photoelectric
effect
3. The number of ejected electrons depend upon
the intensity of light.
Cesium, has lowest ionisation enery and is also the
metal from which electrons are ejected most easily
by light. This metal is, therefore, used largely in
photoelectric cells.
This phenomenon of photoelectric effect explained
by Einstein on basis of quantum theory. According
to this theory, light consists of bundles of energy,
photons, the energy of each photon being equal to
hv , where v is frequency of light. Now suppose
frequency of light falling on a metal surface is
higher than threshold frequency. Let it be v. When
photon of this light strikes a metal surface, some of
its energy is consumed to seperate the electrons
from the metal and

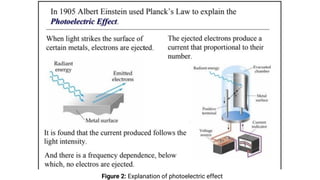
14. ● Photoelectric
effect
remaining energy will be imparted to ejected
electron to give it certain velocity u( i.e, K. E=1/2
mu2
). Einstein applying quantum theory showed
that,
hv = ∅ +1/2mu2
_______1
where ∅ =threshold energy of metal and 1/2mu2
is
K. E imparted to ejected electron.
∅ = hv0
_________2
Substituting the equation 2 in equation 1
1/2 mu2
= h(v-v0)
) ______[Einstein’s
Photoelectric Effect]

15. Plank’s Radiation Law

16. ● Plank’s
Radiation Law
This theory was put forward to explain the
phenomenon of black body radiation and
photoelectric effect.
This theory was given by Max Planck in 1901.
According to this theory,
1. Radiant energy is emitted or absorbed
discontinuously in the form of tiny bundles of
energy known as quanta.
2. Each quantum is associated with a definite
amount of energy E(=hv), where E is the
energy in joules, v is frequency of radiation in
reciprocal seconds(ss-1
) and h is a
fundamental constant known as plank's
constant. The numerical value of h is 6.626
×10-34
s.

17. ● Plank's
Radiation Law
The value of a quantum of energy is also given by
hcν̅ where v
̅ is wave number defined as the
reciprocal of wave length, i.e, v
̅ =(1/λ). Evidently,
v=c/λ=cv
̅ and E=hcv
̅ .
A body can emit or absorb energy only in whole
number multiples of quantum, i. e, 1hv, 2hv,
3hv………, nhv. Energy in fractions of a quantum
cannot be lost or absorbed. This is known as
quantisation of energy.
Based on this theory, plank obtained following
equation for energy density of black body radiation:
E(v)dv=(8πhv³/c³) x (dv/exp(hv / kT)-1
)
This equation accounts for black body radiation
curves at all wavelengths obtained at different
temperatures as in figure 3.

18. Figure 3: Wavelength - intensity relationship

19. Compton Effect

20. ● Compton Effect
Arthur Compton found that if monochromatic
X-rays are allowed to fall on carbon or some other
light element, the scattered X-rays have
wavelenghts larger than incident rays.
In other words, scattered X-rays have lower
frequency, i. e, lower energy than incident X-rays.
Since scattering is caused by electrons, it is evident
that some interaction between X-rays and electrons
has taken place and has resulted in decrease in
energy of former.
This decrease in energy or increase in wavelength
of X-rays after scattering from surface of an object
called compton effect.

21. ● Compton Effect
By applying the law of conservation of energy and
law of conservation of momentum and assuming
X-rays to consists of photons, each possesing
energy equal to hv, compton showed that
Δλ= (2 h/mc)sin²(∅/2) ) _________ 2
Where Δλ is increase in wavelength (termed as
compton shift) produced as a result of collision , m
is rest mass of electron, c is velocity of light and ∅
is angle between incident and scattered X-rays.
According to this equation, compton shift should be
independent of wavelength of incident X-rays.
Compton effect provides a good illustration of
uncertainty principle.

22. ● Compton Effect
Suppose X-rays are used to determine position and
momentum of an electron.
As a result of mutual interaction of X-rays and the
electron, wavelength of X-rays increases, i. e, the
frequency of energy of X-rays decreases.
Compton effect also provides evidence for the
corpuscular Or photon nature of radiation.
The compton equation 1 , can also be written as
λ=λ'-λ=h/mc (1-cos∅) _________3
We see that wavelength λ' of scattered X-rays is
always greater than the wavelength λ of incident
X-rays.

23. ● Compton Effect
The wavelength shift depends only on scattering
angle ∅ . Following three cases are considered :-
Case 1 : ∅=1 , i. e, the scattered radiation is parallel
to incident radiation.
In this case, cos ∅ =1 , so that Δλ=0 , i.e, there is no
wavelength shift.
Case 2: ∅= 90° , i. e, scattered radiation is
perpendicular to incident radiation.
In this case cos ∅ =0, so that,
Δλ=h/mc=6.626x10-34
Js / (9.109×10-31
kg) ×
(3×108
ms-1
)
= 0.02422×10-10
m

24. ● Compton Effect
In the present case, Δλ is referred to as compton
wavelength.
Case 3: ∅=180°, i. e, the radiation is scattered in a
direction opposite to incident radiation. In this case,
cos ∅= -1
Δλ=2h/mc
=0.0484×10-10
This is twice the value of compton wavelength.

25. Thank you