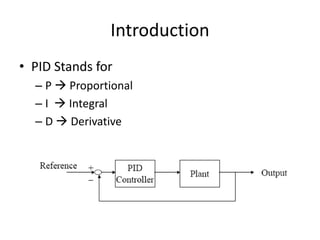
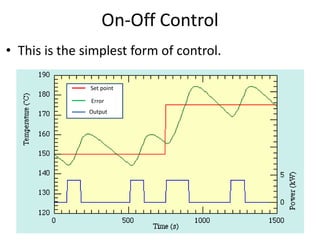
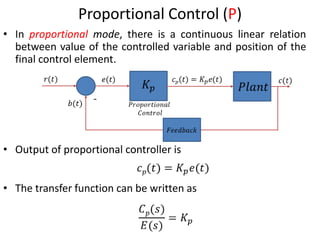
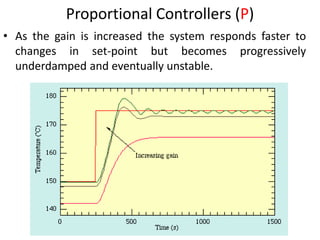
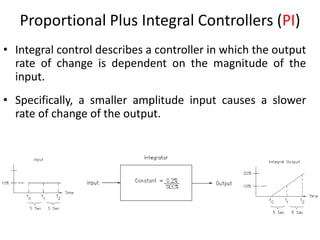
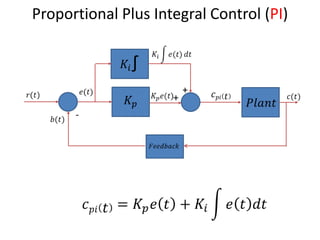
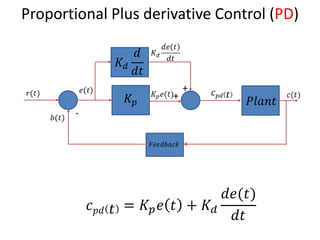
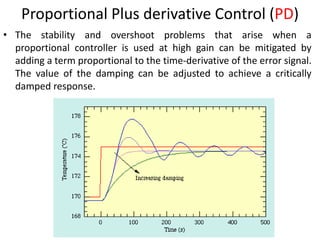
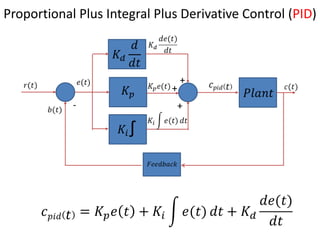
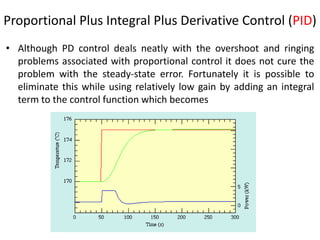
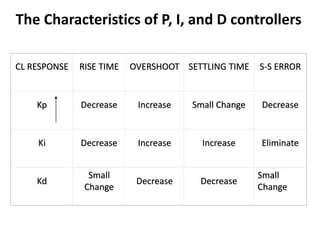
The document discusses PID controllers, detailing their components: Proportional, Integral, and Derivative, and their roles in control systems. It highlights the advantages and disadvantages of each controller type, emphasizing their applicability, tuning methods, and effects on system stability. PID controllers are noted for their widespread use in industry, with over half of existing controllers being PID or modified versions.

1. Control Systems (CS)
Dr. K. Hussain
Associate Professor & Head
Dept. of EE, SITCOE
Unit-5:
PID Controllers

2. Lecture Outline

3. Introduction
• PID Stands for
– P  Proportional
– I  Integral
– D  Derivative

4. Introduction
• The usefulness of PID controls lies in their general
applicability to most control systems.
• In particular, when the mathematical model of the plant
is not known and therefore analytical design methods
cannot be used, PID controls prove to be most useful.
• In the field of process control systems, it is well known
that the basic and modified PID control schemes have
proved their usefulness in providing satisfactory control,
although in many given situations they may not provide
optimal control.

5. Introduction
• It is interesting to note that more than half of the
industrial controllers in use today are PID controllers or
modified PID controllers.
• Because most PID controllers are adjusted on-site, many
different types of tuning rules have been proposed in the
literature.
• Using these tuning rules, delicate and fine tuning of PID
controllers can be made on-site.

6. 6
Four Modes of Controllers
• Each mode of control has specific advantages and
limitations.
• On-Off (Bang Bang) Control
• Proportional (P)
• Proportional plus Integral (PI)
• Proportional plus Derivative (PD)
• Proportional plus Integral plus Derivative (PID)

7. On-Off Control
• This is the simplest form of control.
Set point
Error
Output

8. 8
Proportional Control (P)
• In proportional mode, there is a continuous linear relation
between value of the controlled variable and position of the
final control element.
• Output of proportional controller is
• The transfer function can be written as
-

9. 9
Proportional Controllers (P)
• As the gain is increased the system responds faster to
changes in set-point but becomes progressively
underdamped and eventually unstable.

10. 10
Proportional Plus Integral Controllers (PI)
• Integral control describes a controller in which the output
rate of change is dependent on the magnitude of the
input.
• Specifically, a smaller amplitude input causes a slower
rate of change of the output.

11. 11
Proportional Plus Integral Controllers (PI)
• The major advantage of integral controllers is that they have
the unique ability to return the controlled variable back to the
exact set point following a disturbance.
• Disadvantages of the integral control mode are that it
responds relatively slowly to an error signal and that it can
initially allow a large deviation at the instant the error is
produced.
• This can lead to system instability and cyclic operation. For
this reason, the integral control mode is not normally used
alone, but is combined with another control mode.

12. 12
Proportional Plus Integral Control (PI)
-
+
+

13. 13
Proportional Plus Integral Control (PI)
• The transfer function can be written as

14. 14
Proportional Plus derivative Control (PD)
-
+
+

15. 15
Proportional Plus derivative Control (PD)
• The transfer function can be written as

16. 16
Proportional Plus derivative Control (PD)
• The stability and overshoot problems that arise when a
proportional controller is used at high gain can be mitigated by
adding a term proportional to the time-derivative of the error signal.
The value of the damping can be adjusted to achieve a critically
damped response.

17. 17
Proportional Plus derivative Control (PD)
• The higher the error signal rate of change, the sooner the final
control element is positioned to the desired value.
• The added derivative action reduces initial overshoot of the
measured variable, and therefore aids in stabilizing the process
sooner.
• This control mode is called proportional plus derivative (PD) control
because the derivative section responds to the rate of change of the
error signal

18. 18
Proportional Plus Integral Plus Derivative Control (PID)
-
+
+
+

19. 19
Proportional Plus Integral Plus Derivative Control (PID)

20. Proportional Plus Integral Plus Derivative Control (PID)
• Although PD control deals neatly with the overshoot and ringing
problems associated with proportional control it does not cure the
problem with the steady-state error. Fortunately it is possible to
eliminate this while using relatively low gain by adding an integral
term to the control function which becomes
20

21. P – controller
The transfer function of this controller is KP.
The main disadvantage in P – controllers is that as KP value
increases, decreases & hence overshoot increases.
As overshoot increases system stability decreases.
I – controller
The transfer function of this controller is Ki/s.
It introduces a pole at origin and hence type is increased and
as type increases, the SS error decrease but system stability
is affected.
D – controller
It’s purpose is to improve the stability.
The transfer function of this controller is sKD.
It introduces a zero at origin so system type is decreased but
steady state error increases.
Effect of P,I,PI,PD & PID Controller on systems

22. Effect of P,I,PI,PD and PID on system
• PI – controller
• It’s purpose SS error without affection stability.
• It adds pole at origin, so type increases & SS error decreases.
• It adds a zero in LHP, so stability is not affected.
• Effects:
• o Improves damping and reduces maximum overshoot.
• o Increases rise time.
• o Decreases BW.
• o Improves Gain Margin, Phase margin & Mr.
• o Filter out high frequency noise.

23. PD controller
Its purpose is to improve stability without affecting stability.
Transfer function: KP+sKD
It adds a zero in LHP, so stability improved.
Effects:
o Improves damping and maximum overshoot.
o Reduces rise time & setting time.
o Increases BW.
o Improves GM, PM, Mr.
o May attenuate high frequency noise.
PID controller
Its purpose is to improve stability as well as to decrease ess.
o If adds a pole at origin which increases type & hence
steady state error decreases.
o If adds 2 zeroes in LHP, one finite zero to avoid effect on
stability & other zero to improve stability of system.

24. CL RESPONSE RISE TIME OVERSHOOT SETTLING TIME S-S ERROR
Kp Decrease Increase Small Change Decrease
Ki Decrease Increase Increase Eliminate
Kd
Small
Change
Decrease Decrease
Small
Change
The Characteristics of P, I, and D controllers