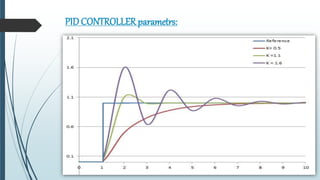
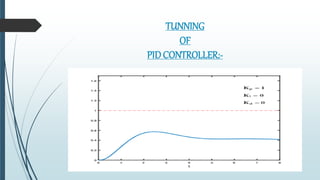
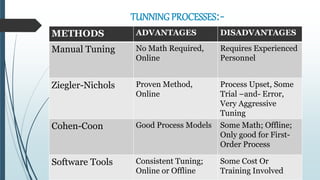
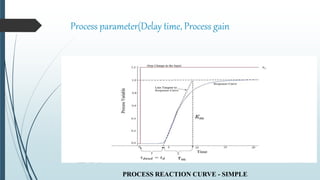
This document discusses tuning PID controllers. It introduces PID controllers and their proportional, integral and derivative terms. It describes different tuning methods, focusing on the Ziegler-Nicolas tuning method. This method relates process parameters like delay time and gain to PID parameters. It involves adjusting the proportional band until oscillations occur, then using those values to calculate initial PID settings according to provided tables. The goal of tuning is to optimize rise time, overshoot, settling time, steady state error and stability.

1. TUNING
OF
PID CONTROLLER
Submitted by:
SUBHANKAR SAU
1401216049
EEE Department
Guided by:-
Prof. P.K. Panigrahi(H.O.D)
Prof. Siddheswar Kar
Prof. Debasis Choudhury
Prof. Sarat ku. Mishra

2. CONTENTS:-
INTRODUCTION
PID CONTROLLER
TUNNING PROCESS
DIFFERENT TUNING METHODS
ZIEGLER-NICOLAS TUNNING METHOD
CONCLUSION

3. I N T R O D U C T I O N : -
 The Controller: It decides the control variable in order to bring the process
variable as close as to the set point.
 PID controller: It continuously calculates an error value e(t) as the difference
between a desired set point and a measured process variable and applies a
correction based on proportional ,integral and derivative terms which give their to
controller types.

4. PID Controller:-
 Proportional Term(P): It is a constant directly related to the amount of the error. If you have
large error ,the term gives you a large output, and if you have a small error, it will give you a
small output. In simple term affects the speed to reach your target.
 Integral Term(I): It is constant related to integration(summation) of errors over time. If your
error is increasing, this term gives you a large output. However if the error is decreasing, the I
term give you a small output. Thus it is used to fine tune your results i.e. when you almost reach
your goal, the P term can not serve you any more.
 Derivative Term(D): It is constant related to the rate of change of errors with time. i.e you have
a highly dynamic systems like a multi-coptor, the D-term will give you higher output to catch up
with the changes.

5. NEED
OF
PID CONTROLLER:-
PARAMETER RISE TIME OVERSHOO
T
SETTLING
TIME
STEADY-
STATE
ERROR
STABILITY
Kp Decrease Increase Small
Change
Decrease Degrade
Ki Decrease Increase Increase Eliminate Degrade
Kd Minor
Change
Decrease Decrease No Effect Improve if
Kd Small

6. PID CONTROLLER parametrs:

7. TUNING PROCEDURES OF
PID CONTROLLER:-
1) After nulling all the parameters ,increase the P term so that the output reaches the
target in shortest possible time.
2) If your output starts oscillating ,it means you have too much P. lower your P term
until the oscillation disappears. You will end up slightly higher or lower than
your target.
3) Now increase I term slightly until your errors goes away. Note that usual I values
are very small and they are dependent on the update rate of your PID loop. If you
feel your output is oscillating lower your I term.
4) Now for highly dynamic system we need to adjust the D term also.
5) If your system starts oscillating with high frequency and small transition it
means we have too much D term which is amplifying the noise. If it has too
much noise its better to keep the D parameter to zero.
6) At last watch your limits . If you are changing the previous parameters without
any noticeable change in the output
This Completes the tuning procedure of the PID Controller.

8. TUNNING
OF
PID CONTROLLER:-

9. TUNNING PROCESSES:-
METHODS ADVANTAGES DISADVANTAGES
Manual Tuning No Math Required,
Online
Requires Experienced
Personnel
Ziegler-Nichols Proven Method,
Online
Process Upset, Some
Trial –and- Error,
Very Aggressive
Tuning
Cohen-Coon Good Process Models Some Math; Offline;
Only good for First-
Order Process
Software Tools Consistent Tuning;
Online or Offline
Some Cost Or
Training Involved

10. ZIEGLER-NICHOLUS METHOD
(OpenloopMethod):-
 It is done in manual mode.
 It is way of relating the process parameters(i.e Controller gain & Reset time).
 It has been developed for use on delay-followed by first-order-lag-processes.
 Once the value of process parameters are obtained the PID parameters can be
calculated from the below table.

11. Process parameter(Delay time, Process gain
PROCESS REACTION CURVE - SIMPLE

12. ZIEGLER-NICHOLUS METHOD
(CloseloopMethod):-continue
 In controller automatic mode(operating condition), PV approximate to set point, change the
%PB of controller to maximum, Integral time maximum and Derivative time minimum,
then decrease %PB and take load step(change set-point or process loads) for monitor PV
responding until PV occur slight oscillation. Record %PB of Oscillate condition(Ultimate
controller gain ,Kcu) and Band width( ultimate period ,Pu).

13. ZIEGLER-NICHOLUS METHOD
(closeloopMethod):-continue
 Then we roughly tune the initial value as the below table;
Where
Kc= Controller gain
%PB= 1/Kc x 100(%)
%PB=% Proportional Band
Ti= Integral Time or Reset time
(Sec./Repeat)
Td= Derivative time or rate
(Sec.)

14. CONCLUSION:-
P Controller mitigates error but initiates offset.
I Controller mitigates offset but initiates overshoot.
D Controller mitigates overshoot for optimization.