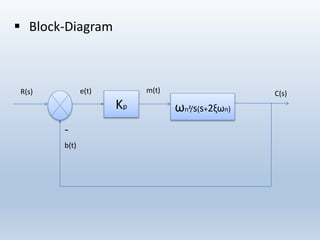
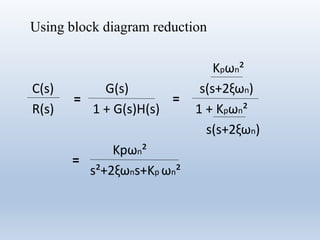
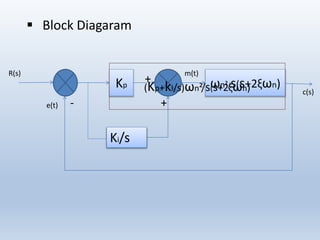
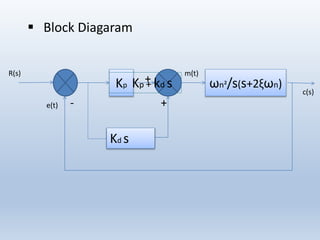
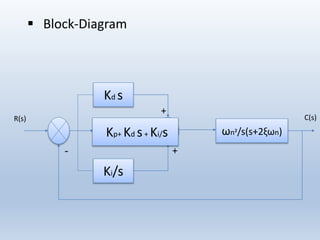
The document discusses different types of controllers: 1) On-Off, P, PI, PD, and PID controllers. On-Off controllers have only two modes while P controllers use proportional gain. PI controllers add integral action to eliminate steady-state error. PD controllers use derivative action and PID controllers combine all three actions. 2) Block diagrams and transfer functions are presented to show how each controller type is modeled and its effect on the closed loop system. The proportional, integral, and derivative gains (Kp, Ki, Kd) determine each controller's effect. 3) PID controllers combine proportional, integral and derivative actions and are commonly used in industrial control systems due to their robust performance.

1. Prepared By:
Kishan Beldiya (140040109002)
Jaydeep Chandra (140040109009)
5th Sem., EE. Engg. Dept.,
BHGCET, Rajkot
Internal Guide:
Prof. Nirav B Mehta
Electrical Dept.
BHGCET, Rajkot
Presentation on
Types Of Controller
Under the subject of
Control System Engineering

2. Types Of Controller
• On-Off Controller
• P Controller
• PI Controller
• PD Controller
• PID controller

3. On-Off Controller
• On-Off control is the simplest form of feedback
control and it has only two mode.
• A common example of on-off control is the
temperature control in a domestic heating system.

4. P Controller
• To Understand P Controller We Need a Model
Velocity
Gas paddle

5. P Controller
• The relationship between the error signal and
controller output
m(t)=Kpe(t)+m0
Here , m(t)=Controller output,
e(t)=error
Kp=Proportional gain constant
m0=Controller output at zero error

6.  Block-Diagram
Kp ωn²/s(s+2ξωn)
R(s) e(t) m(t)
b(t)
C(s)
-

7. Kpωn²
C(s) G(s) s(s+2ξωn)
R(s) 1 + G(s)H(s) 1 + Kpωn²
s(s+2ξωn)
Kpωn²
s²+2ξωns+Kp ωn²
= =
=
Using block diagram reduction

8. PI Controller
The integral action is given by,
mi(t) = ki ∫e(t)dt+ m(0)
Mathematical expression for P-I controller
m(t)=kpe(t) + ki∫e(t)dt + m(0)

9. Kp ωn²/s(s+2ξωn)
e(t)
c(s)
m(t)
-
Kp∫dtKi/s
+
+
R(s)
(Kp+ki/s)ωn²/s(s+2ξωn)
 Block Diagaram

10. We use Block Diagram Reduction Techniques
C(s) G(s)
R(s) 1 + G(s)H(s)
(Kp s + Ki)ωn²
s³ + 2ξs²ωn +Kp ωn²+Ki ωn²
=
=

11. P-D Controller
The derivation action is given by,
md(t)=Kd
𝑑
𝑑𝑡
e(t)
mathematical expression for P-D Controller is
m(t)=Kpe(t)+ Kd
𝑑
𝑑𝑡
e(t)+m0
Now take laplace,
M(s)=KpE(s) + Kd sE(s)+M0

12. Kp ωn²/s(s+2ξωn)
e(t)
c(s)
m(t)
-
Kd 𝑑/𝑑𝑡Kd s
+
+
R(s)
Kp + kd s
 Block Diagaram

13. • Hence the T.f is ,
C(s) G(s)
R(s) 1 + G(s)H(s)
=
= (Kp s + Ki)ωn²
s² + 2ωn(ξ+kdωn )+Kp ωn²
2
C(s)
R(s)

14. mathematical expression for P-I-D Controller
m(t)=Kpe(t)+ ki ∫e(t)dt+ Kd
𝑑
𝑑𝑡
e(t)+m0
Now take laplace
M(s)=KpE(s) +Ki Es +Kd sE(s)+M0
s
PID Controller

15. Kp
Kd s
Ki/s
ωn²/s(s+2ξωn)
R(s)
-
+
+
+
C(s)
Kp+ Kd s+ Ki/s
 Block-Diagram

16. Hence the T.f is ,
C(s) G(s)
R(s) 1 + G(s)H(s)
=
C(s) (Kds²+kps+ki) ωn²
R(s) 𝑆3 + (2ξωn+kdωn² ) s²+Kp ωn²s
=