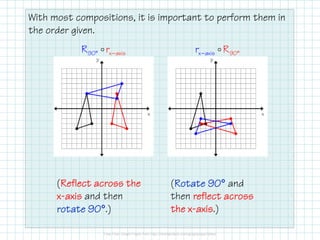
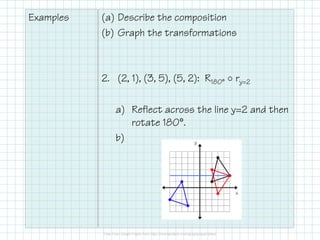
The document discusses compositions of transformations, which involve performing two or more transformations sequentially on a figure. It provides examples of compositions, such as a glide reflection, which reflects a figure and then translates it. Compositions are described using notation listing the transformations from right to left. Most compositions are important to perform in the given order. Examples are provided to describe and graph compositions involving reflections across axes or lines combined with translations or rotations.

1. Obj. 32 Compositions
The student is able to (I can):
• Draw and identify compositions of transformations

2. composition of
Performing two or more transformations
transformations sequentially (one after another) to a
figure.
An example that we have already seen of
a composition is a glide reflection: we
reflect the figure and then translate it
along a vector.

3. To describe a composite transformation
using notation, state each of the
transformations that make up the
composite transformation and link them
with the symbol . The transformations are
performed in order from right to left
left.
Example: To perform the transformation
T2,4 R 90° rx −axis
rx-axis — Reflect across the x-axis
R90° — Rotate 90° counterclockwise
T2, 4 — Translate along the vector 〈2, 4〉

4. With most compositions, it is important to perform them in
the order given.
R 90° rx −axis
(Reflect across the
Reflect
x-axis and then
90°
rotate 90°.)
rx −axis R 90°
(Rotate 90° and
Rotate 90°
then reflect across
x-axis.)
the x-axis

5. Examples
(a) Describe the composition
(b) Graph the transformations
1. (1, 4), (—2, 1), (—4, 1): T—3, 1
ry-axis
2. (2, 1), (3, 5), (5, 2): R180°
ry=2

6. Examples
(a) Describe the composition
(b) Graph the transformations
1. (1, 4), (—2, 1), (—4, 1): T—3, 1
ry-axis
a) Reflect across the y-axis and
translate along the vector 〈—3, 1〉
b)

7. Examples
(a) Describe the composition
(b) Graph the transformations
2. (2, 1), (3, 5), (5, 2): R180°
ry=2
a) Reflect across the line y=2 and then
rotate 180°.
b)