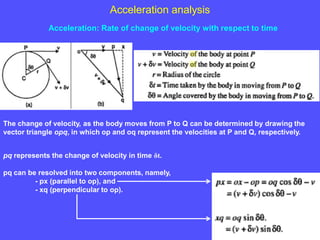
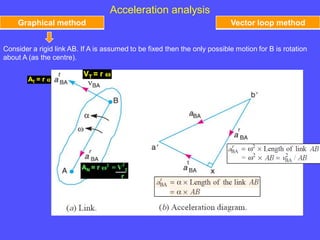
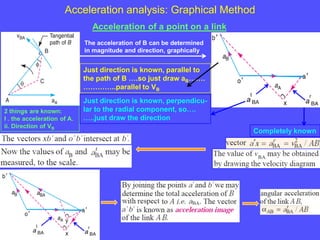
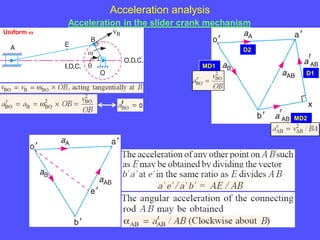
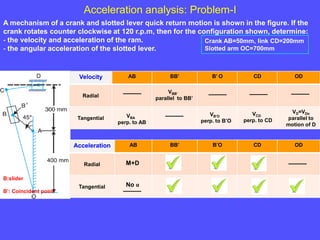
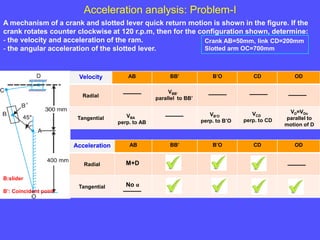
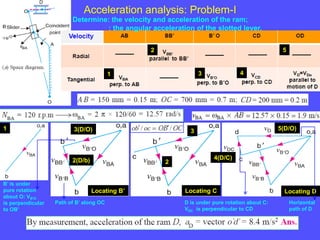
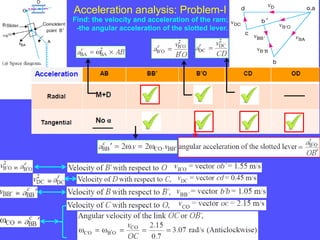
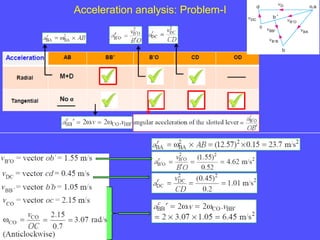
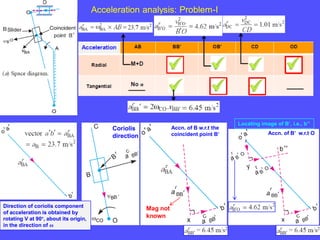
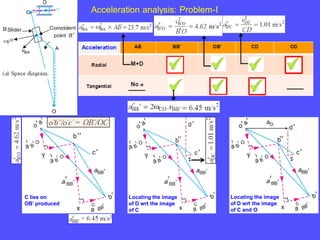
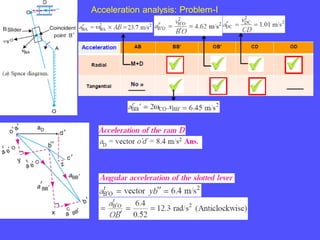
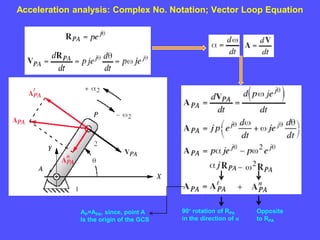
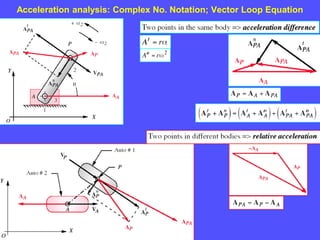
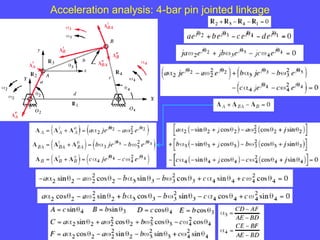
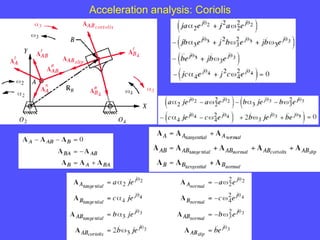
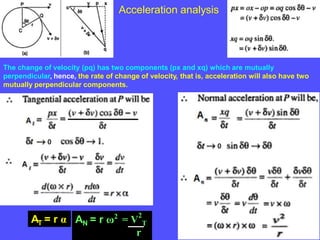
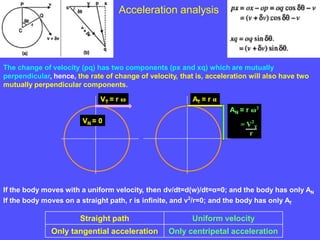
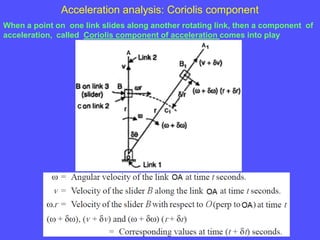
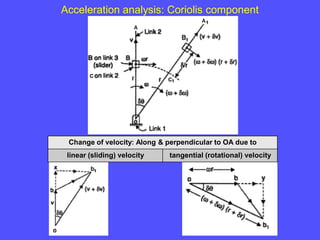
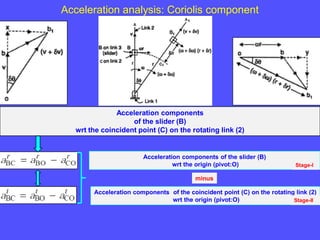
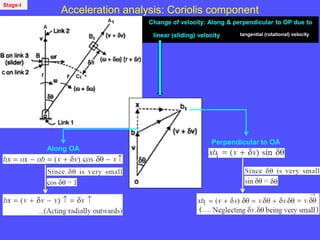
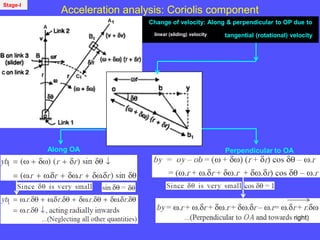
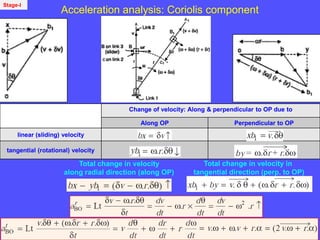
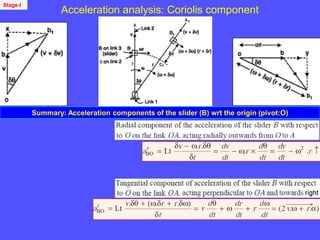
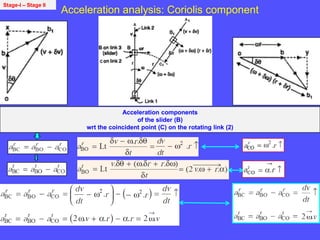
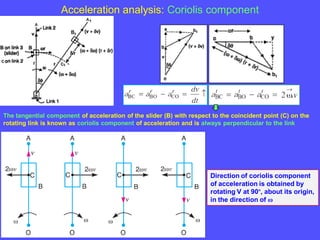
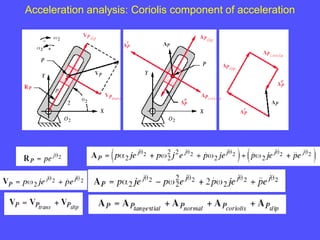
1) To analyze accelerations, positions must first be found to calculate velocities by differentiation and accelerations by further differentiation. 2) Acceleration has two components - tangential and centripetal. For uniform motion only centripetal acceleration exists, and for straight-line motion only tangential acceleration exists. 3) The Coriolis component arises for points moving on rotating links and is perpendicular to the link and proportional to the product of linear and angular velocities.

1. Kinematic Analysis: Scope
•Need to know the dynamic forces to be able to compute stresses in the components
• Dynamic forces are proportional to acceleration (Newton second law)
• Goal shifts to finding acceleration of all the moving parts in the assembly
•In order to calculate the accelerations:
• need to find the positions of all the links , for all increments in input motion
• differentiate the position eqs. to find velocities, diff. again to get accelerations

2. Acceleration analysis
Acceleration: Rate of change of velocity with respect to time
The change of velocity, as the body moves from P to Q can be determined by drawing the
vector triangle opq, in which op and oq represent the velocities at P and Q, respectively.
pq represents the change of velocity in time δt.
pq can be resolved into two components, namely,
- px (parallel to op), and
- xq (perpendicular to op).

3. Acceleration analysis
The change of velocity (pq) has two components (px and xq) which are mutually
perpendicular, hence, the rate of change of velocity, that is, acceleration will also have two
mutually perpendicular components.
AT = r α AN = r ω2
= V
2
T
r

4. Acceleration analysis
The change of velocity (pq) has two components (px and xq) which are mutually
perpendicular, hence, the rate of change of velocity, that is, acceleration will also have two
mutually perpendicular components.
If the body moves with a uniform velocity, then dv/dt=d(w)/dt=α=0; and the body has only AN
If the body moves on a straight path, r is infinite, and v2
/r=0; and the body has only AT
Straight path Uniform velocity
Only tangential acceleration Only centripetal acceleration

5. Acceleration analysis
Graphical method Vector loop method
Consider a rigid link AB. If A is assumed to be fixed then the only possible motion for B is rotation
about A (as the centre).

6. Acceleration analysis: Graphical Method
Acceleration of a point on a link
2 things are known:
I . the acceleration of A.
ii. Direction of VB
The acceleration of B can be determined
in magnitude and direction, graphically
Completely known
Just direction is known, perpendicu-
lar to the radial component, so….
…..just draw the direction
Just direction is known, parallel to
the path of B ….so just draw aB…….
…………..parallel to VB

7. Acceleration analysis
Acceleration in the slider crank mechanism
Uniform ω
MD2
MD1
D1
D2

8. Acceleration analysis: Coriolis component
When a point on one link slides along another rotating link, then a component of
acceleration, called Coriolis component of acceleration comes into play

9. Acceleration analysis: Coriolis component
Change of velocity: Along & perpendicular to OA due to
linear (sliding) velocity tangential (rotational) velocity

10. Acceleration analysis: Coriolis component
Acceleration components
of the slider (B)
wrt the coincident point (C) on the rotating link (2)
Acceleration components of the coincident point (C) on the rotating link (2)
wrt the origin (pivot:O)
Acceleration components of the slider (B)
wrt the origin (pivot:O)
minus
Stage-I
Stage-II

11. Acceleration analysis: Coriolis component
Change of velocity: Along & perpendicular to OP due to
linear (sliding) velocity tangential (rotational) velocity
Along OA
Perpendicular to OA
Stage-I

12. Acceleration analysis: Coriolis component
Change of velocity: Along & perpendicular to OP due to
linear (sliding) velocity tangential (rotational) velocity
Along OA Perpendicular to OA
Stage-I

13. Acceleration analysis: Coriolis component
Change of velocity: Along & perpendicular to OP due to
Along OP Perpendicular to OP
linear (sliding) velocity
tangential (rotational) velocity
Total change in velocity
along radial direction (along OP)
Total change in velocity in
tangential direction (perp. to OP)
Stage-I

14. Acceleration analysis: Coriolis component
Summary: Acceleration components of the slider (B) wrt the origin (pivot:O)
Stage-I

15. Acceleration analysis: Coriolis component
Summary: Acceleration components of the coincident point (C) on the rotating link (2) wrt O
Stage-II

16. Acceleration analysis: Coriolis component
Stage-I – Stage II
Acceleration components
of the slider (B)
wrt the coincident point (C) on the rotating link (2)

17. Acceleration analysis: Coriolis component
The tangential component of acceleration of the slider (B) with respect to the coincident point (C) on the
rotating link is known as coriolis component of acceleration and is always perpendicular to the link
Direction of coriolis component
of acceleration is obtained by
rotating V at 90º, about its origin,
in the direction of ω

18. Acceleration analysis: Problem-I
A mechanism of a crank and slotted lever quick return motion is shown in the figure. If the
crank rotates counter clockwise at 120 r.p.m, then for the configuration shown, determine:
- the velocity and acceleration of the ram.
- the angular acceleration of the slotted lever.
Crank AB=50mm, link CD=200mm
Slotted arm OC=700mm
Velocity AB BB’ B’ O CD OD
Radial
Tangential
Acceleration AB BB’ B’O CD OD
Radial
Tangential
___
VBA
perp. to AB
___
___ ___ ___VBB’
parallel to BB’
VB’O
perp. to B’O
VCD
perp. to CD
VD=VDo
parallel to
motion of D
___No α
M+D ___
B:slider
B’: Coincident point

19. Acceleration analysis: Problem-I
A mechanism of a crank and slotted lever quick return motion is shown in the figure. If the
crank rotates counter clockwise at 120 r.p.m, then for the configuration shown, determine:
- the velocity and acceleration of the ram.
- the angular acceleration of the slotted lever.
Crank AB=50mm, link CD=200mm
Slotted arm OC=700mm
Velocity AB BB’ B’O CD OD
Radial
Tangential
Acceleration AB BB’ B’O CD OD
Radial
Tangential
___
VBA
perp. to AB
___
___ ___ ___VBB’
parallel to BB’
VB’O
perp. to B’O
VCD
perp. to CD
VD=VDo
parallel to
motion of D
___No α
M+D ___
B:slider
B’: Coincident point

20. Acceleration analysis: Problem-I
Determine: the velocity and acceleration of the ram;
: the angular acceleration of the slotted lever.
1
1
Locating B’
2(D/b)
3(D/O)
2
3
B’ is under
pure rotation
about O: VB’O
is perpendicular
to OB’
Path of B’ along OC
2
3
Locating C
4
5
4
5
Locating D
4(D/C)
5(D/O)
D is under pure rotation about C:
VDC is perpendicular to CD
Horizontal
path of D

21. Acceleration analysis: Problem-I
Find: the velocity and acceleration of the ram;
-the angular acceleration of the slotted lever.

22. Acceleration analysis: Problem-I

23. Acceleration analysis: Problem-I
Coriolis
direction
Direction of coriolis component
of acceleration is obtained by
rotating V at 90º, about its origin,
in the direction of ω
Mag not
known
Accn. of B w.r.t the
coincident point B’
Locating image of B’, i.e., b’’
Accn. of B’ w.r.t O

24. Locating the image
of D wrt the image
of C
C lies on
OB’ produced
Acceleration analysis: Problem-I
Locating the image
of D wrt the image
of C and O

25. Acceleration analysis: Problem-I

26. Acceleration analysis: Complex No. Notation; Vector Loop Equation
90º rotation of RPA
in the direction of α
Opposite
to RPA
AP=APA, since, point A
Is the origin of the GCS

27. Acceleration analysis: Complex No. Notation; Vector Loop Equation

28. Acceleration analysis: 4-bar pin jointed linkage

29. Acceleration analysis: 4-bar slider crank

30. Acceleration analysis: Coriolis component of acceleration

31. Acceleration analysis: Coriolis

32. Acceleration analysis: Coriolis