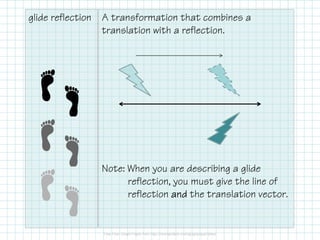
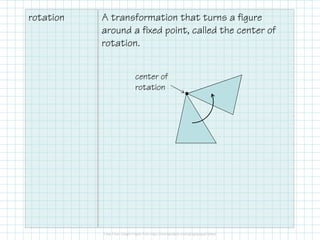
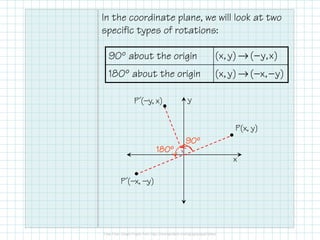
This document defines and provides examples of glide reflections and rotations. It explains that a glide reflection combines a translation with a reflection along a line, and a rotation turns a figure around a fixed center point. The document also gives the specific formulas for rotating a point 90 and 180 degrees around the origin, and provides examples of applying each rotation to triangles defined by sets of coordinates.

1. Obj. 31 Glide Reflections & Rotations
The student is able to (I can):
• Identify and draw glide reflections
• Identify and draw rotations

2. glide reflection A transformation that combines a
translation with a reflection.
Note: When you are describing a glide
reflection, you must give the line of
reflection and the translation vector.

3. rotation
A transformation that turns a figure
around a fixed point, called the center of
rotation.
center of
rotation
•

4. In the coordinate plane, we will look at two
specific types of rotations:
90º about the origin
(x, y) → (− y, x)
180º about the origin
(x, y) → (− x, − y)
P´(—y, x)
•
180º
y
90º
•
P(x, y)
x
•
P´(—x, —y)

5. Examples
1. Rotate ∆RUG with vertices R(2, -1),
U(4, 1), and G(3, 3) by 90º about the
origin.
(x, y) → (− y, x)
90º:
U´
G´
R´(1, 2), U´(-1, 4), G´(-3, 3)
2. Rotate ∆TRI with vertices T(2, 2),
R(4, -5), and I(-1, 6) by 180º about the
origin.
(x, y) → (− x, − y)
180º:
R´
I´
T´(-2, -2), R´(-4, 5), I´(1, -6)