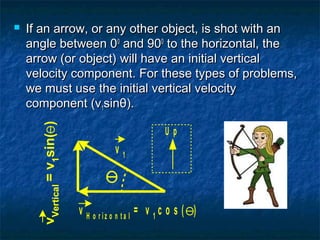
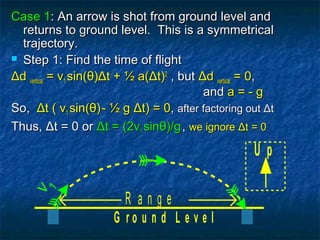
This document discusses vertical projectile motion with an initial vertical velocity component. It provides examples of how to calculate time of flight, maximum height, and range for objects moving under gravity, such as arrows shot at an angle. It includes sample problems and solutions, as well as references to online video explanations and additional practice problems from other sources. Key concepts covered are the use of initial vertical velocity, quadratic equations to solve for time of flight if maximum height is not zero, and how to determine if a trajectory is symmetrical or not.

1. Vertical Projectile Motion
With An Initial Vertical
Velocity Component
Nelson TB Reference Pages:Nelson TB Reference Pages:
78 (1/3 down) - 81 (1/3 down)78 (1/3 down) - 81 (1/3 down)

2.  If an arrow, or any other object, is shot with anIf an arrow, or any other object, is shot with an
angle between 0angle between 000
and 90and 9000
to the horizontal, theto the horizontal, the
arrow (or object) will have an initial verticalarrow (or object) will have an initial vertical
velocity component. For these types of problems,velocity component. For these types of problems,
we must use the initial vertical velocitywe must use the initial vertical velocity
component (vcomponent (v11sinsinθθ))..
v H o r i z o n t a l = v 1 c o s ( )
vVertical=v1sin()
v 1
U p

3. Case 1Case 1: An arrow is shot from ground level and: An arrow is shot from ground level and
returns to ground level. This is a symmetricalreturns to ground level. This is a symmetrical
trajectory.trajectory.
 Step 1: Find the time of flightStep 1: Find the time of flight
ΔΔdd verticalvertical = v= v11 sin(sin(θθ))ΔΔt + ½ a(t + ½ a(ΔΔt)t)22
, but, but ΔΔdd verticalvertical = 0= 0,,
andand a = - ga = - g
So,So, ΔΔt ( vt ( v11 sin(sin(θθ))- ½ g- ½ g ΔΔt) = 0t) = 0,, after factoring outafter factoring out ΔΔtt
Thus,Thus, ΔΔt = 0 ort = 0 or ΔΔt = (2vt = (2v11 sinsinθθ)/g)/g,, we ignorewe ignore ΔΔt = 0t = 0
G r o u n d L e v e l
U p
R a n g e
v
1

4.  We can now calculate the range:We can now calculate the range:
R =R = ((vv11 coscosθθ))ΔΔt =t = ((vv11 coscosθθ))(2v(2v11 sinsinθθ)/g)/g
R =R = (2(2vv11
22
coscosθθsinsinθθ)/g)/g, but, but 2sin2sinθθ·cos·cosθθ = sin2= sin2θθ
So, R = (vSo, R = (v11
22
sin(2sin(2θθ)) / g,)) / g, from this equation we can seefrom this equation we can see
that the greatest range is achieved whenthat the greatest range is achieved when θθ = ____ .= ____ .
 To find the maximum height, we would use:To find the maximum height, we would use:
 ΔΔt = 0.5·(2vt = 0.5·(2v11 sinsinθθ)/g)/g= (v= (v11 sinsinθθ)/g, this value is just half of)/g, this value is just half of
the total time of flight (the total time of flight (symmetrical trajectory onlysymmetrical trajectory only))
 ΔΔddmax-verticalmax-vertical ==,,( v( v11 sinsinθθ)/g )·[(v)/g )·[(v11 sinsinθθ)x ½],)x ½],{{ΔΔd = vd = vavav xx ΔΔt }t }
 The square brackets represents the average vertical velocityThe square brackets represents the average vertical velocity
from ground level to the highest point reachedfrom ground level to the highest point reached
(where v(where vverticalvertical = 0)= 0)
 ΔΔddmax-verticalmax-vertical = ( v= ( v11
22
sinsin22
θθ)/(2g ))/(2g )

5. Case 2Case 2 – Not a Symmetrical Trajectory– Not a Symmetrical Trajectory
 In the diagram, we see that the arrow achieves a finalIn the diagram, we see that the arrow achieves a final
height of “h”. When we calculate the time of flight, weheight of “h”. When we calculate the time of flight, we
would get two different and correct values.would get two different and correct values. OneOne valuevalue
would represent the arrow reaching height “h” on the waywould represent the arrow reaching height “h” on the way
up ( at “A”). Theup ( at “A”). The secondsecond time value occurs when thetime value occurs when the
arrow reaches the same height on the way down (at “B”).arrow reaches the same height on the way down (at “B”).
To know which value is correct, more information wouldTo know which value is correct, more information would
have to be given (range, achieving max height, etc.).have to be given (range, achieving max height, etc.).
 To find time of flight, in this example, a quadratic equationTo find time of flight, in this example, a quadratic equation
would have to be solved since hwould have to be solved since h ≠≠ 00
((h = 0 only for a symmetrical trajectoryh = 0 only for a symmetrical trajectory).).
R a n g e
v1
h
A B

6. Chalkboard Example
 An arrow is shot with an initial velocity ofAn arrow is shot with an initial velocity of 10.0 m/s
[300
Up from Horiz.] from a bridge which isfrom a bridge which is 10.0 m
above the ground. Lettingabove the ground. Letting g = 10.0 m/s2
,,
determine the following:determine the following:
1.1. Time of flightTime of flight
2.2. Maximum height above the groundMaximum height above the ground
3.3. RangeRange [Ans. 2.0 s, hmax= 11.2 m, R = 17.4 m]
G r o u n d L e v e l
v 1
R a n g eh
U p
h M a x

7. Videos
Very short

http://www.youtube.com/watch?v=ZBfy-MNgtoYhttp://www.youtube.com/watch?v=ZBfy-MNgtoY
Shooting at a toy monkey which drops from a tree
– where do you aim?

http://www.youtube.com/watch?v=cxvsHNRXLjwhttp://www.youtube.com/watch?v=cxvsHNRXLjw
Long lesson-type video not shown in class.
 http://www.youtube.com/watch?v=-uUsUaPJUc0http://www.youtube.com/watch?v=-uUsUaPJUc0
Physics PM Rap!
 http://www.youtube.com/watch?v=3X5-nsbPz88http://www.youtube.com/watch?v=3X5-nsbPz88

8. Practice Problems
Nelson TB:
Page 81
#3, 4 (assume no air resistance), 6, 7, 8
Page 93 #41 {Consider ground level as being the
height at which the ball leaves the barrel.}
For additional practice, students should try the
following McGraw-Hill problems found in the
workbook (New Page 42):
#9-12#9-12