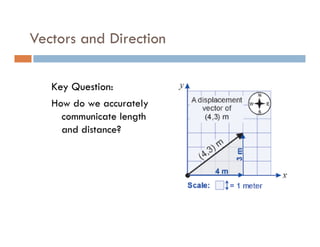
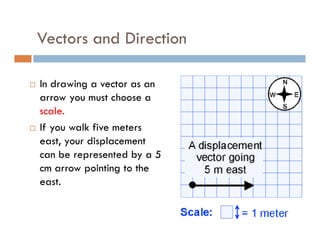
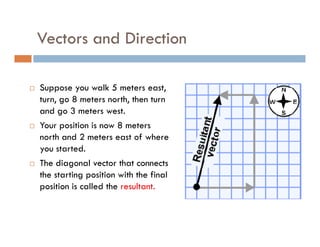
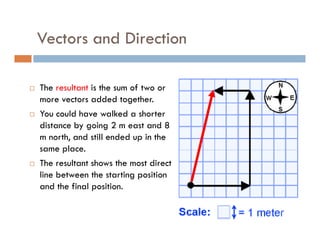
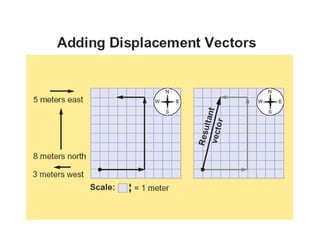
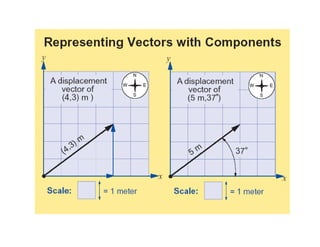
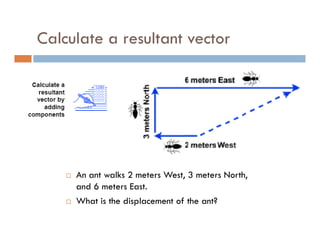
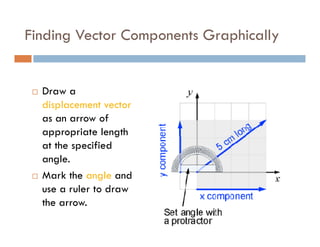
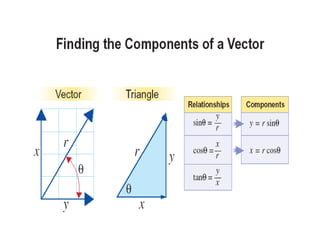
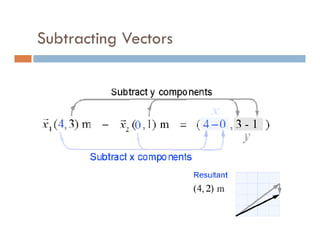
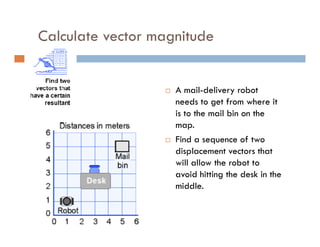
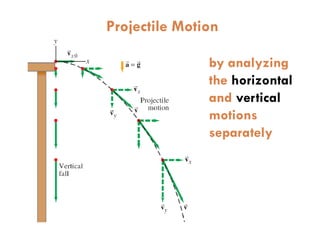
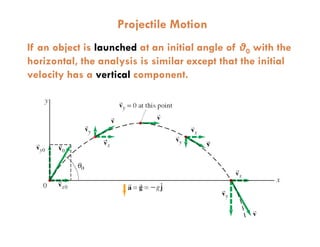
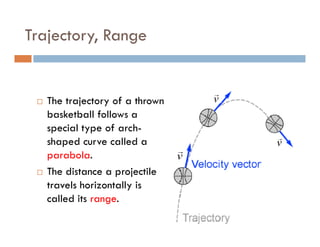
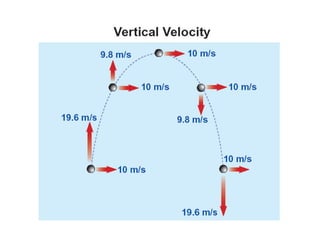
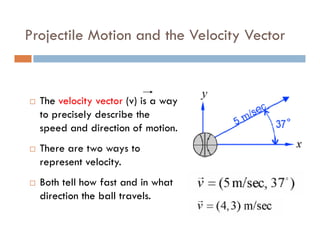
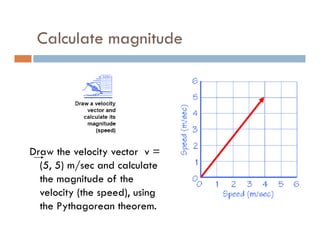
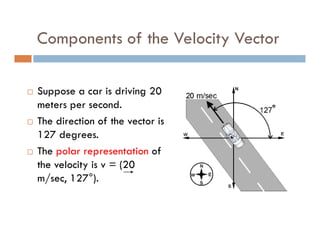
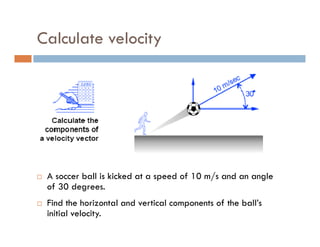
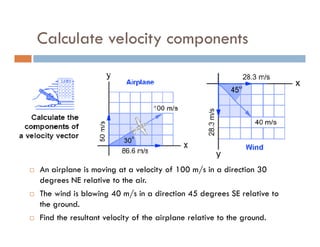
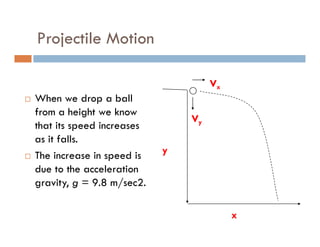
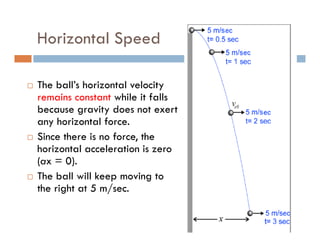
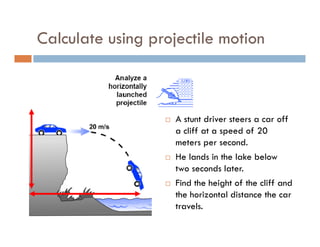
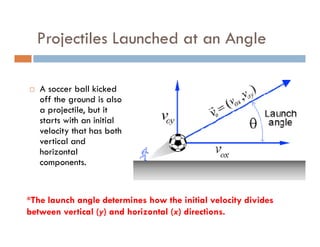
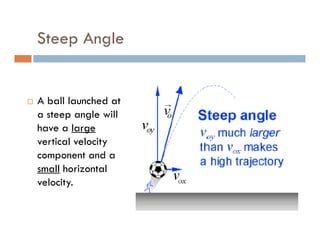
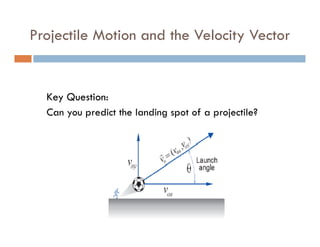
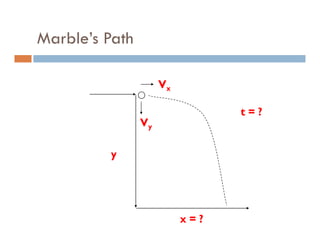
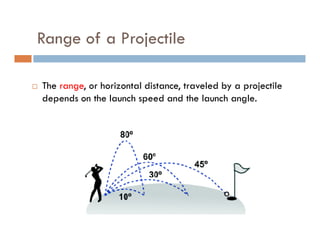
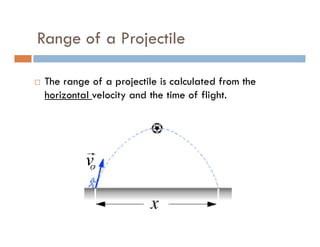
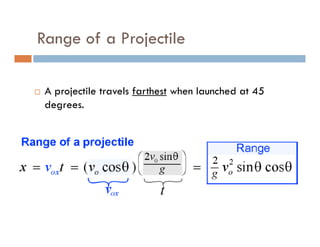
1) A projectile's path is determined by its initial velocity components in the horizontal and vertical directions. 2) The time of flight of a projectile can be calculated from its maximum height using the equation t = √(2y/g). 3) Knowing the time of flight and horizontal velocity component allows calculating the horizontal range using the equation x = vot.

1. VECTORS
PROJECTILE MOTION

2. Vectors and Direction
Key Question:
How do we accurately
communicate length
and distance?

3. Vectors and Direction
A scalar is a quantity that
can be completely described
by one value: the magnitude.
You can think of magnitude
as size or amount, including
units.

4. Vectors and Direction
A vector is a quantity that
includes both magnitude and
direction.
Vectors require more than
one number.
The information “1 kilometer,
40 degrees east of north” is
an example of a vector.

5. Vectors and Direction
In drawing a vector as an
arrow you must choose a
scale.
If you walk five meters
east, your displacement
can be represented by a 5
cm arrow pointing to the
east.

6. Vectors and Direction
Suppose you walk 5 meters east,
turn, go 8 meters north, then turn
and go 3 meters west.
Your position is now 8 meters
north and 2 meters east of where
you started.
The diagonal vector that connects
the starting position with the final
position is called the resultant.

7. Vectors and Direction
The resultant is the sum of two or
more vectors added together.
You could have walked a shorter
distance by going 2 m east and 8
m north, and still ended up in the
same place.
The resultant shows the most direct
line between the starting position
and the final position.

10. Calculate a resultant vector
An ant walks 2 meters West, 3 meters North,
and 6 meters East.
What is the displacement of the ant?

11. Finding Vector Components Graphically
Draw a
displacement vector
as an arrow of
appropriate length
at the specified
angle.
Mark the angle and
use a ruler to draw
the arrow.

13. Finding the Magnitude of a Vector
When you know the x- and y- components of a vector, and the
vectors form a right triangle, you can find the magnitude using
the Pythagorean theorem.

14. Adding Vectors
Writing vectors in components make it easy to add them.

15. Subtracting Vectors

16. Calculate vector magnitude
A mail-delivery robot
needs to get from where it
is to the mail bin on the
map.
Find a sequence of two
displacement vectors that
will allow the robot to
avoid hitting the desk in the
middle.

17. Projectile Motion
A projectile is an
object moving in
two dimensions
under the influence
of Earth's gravity;
its path is a
parabola.

18. Projectile Motion
by analyzing
the horizontal
and vertical
motions
separately

19. Projectile Motion
The speed in the x-
direction is constant; in
the y-direction the object
moves with constant
acceleration g.
This photograph shows two balls that
start to fall at the same time. The one
on the right has an initial speed in the
x-direction. It can be seen that vertical
positions of the two balls are identical
at identical times, while the horizontal
position of the yellow ball increases
linearly.

20. Projectile Motion
If an object is launched at an initial angle of θ0 with the
horizontal, the analysis is similar except that the initial
velocity has a vertical component.

21. Trajectory
The path a projectile
follows is called its
trajectory.

22. Trajectory, Range
The trajectory of a thrown
basketball follows a
special type of arch-
shaped curve called a
parabola.
The distance a projectile
travels horizontally is
called its range.

24. Projectile Motion and the Velocity Vector
The velocity vector (v) is a way
to precisely describe the
speed and direction of motion.
There are two ways to
represent velocity.
Both tell how fast and in what
direction the ball travels.

25. Calculate magnitude
Draw the velocity vector v =
(5, 5) m/sec and calculate
the magnitude of the
velocity (the speed), using
the Pythagorean theorem.

26. Components of the Velocity Vector
Suppose a car is driving 20
meters per second.
The direction of the vector is
127 degrees.
The polar representation of
the velocity is v = (20
m/sec, 127°).

27. Calculate velocity
A soccer ball is kicked at a speed of 10 m/s and an angle
of 30 degrees.
Find the horizontal and vertical components of the ball’s
initial velocity.

28. Adding Velocity Components
Sometimes the total velocity of an object is a combination of
velocities.
One example is the motion of a boat on a river.
The boat moves with a certain velocity relative to the
water.
The water is also moving with another velocity relative to
the land.

29. Adding Velocity Components

30. Calculate velocity components
An airplane is moving at a velocity of 100 m/s in a direction 30
degrees NE relative to the air.
The wind is blowing 40 m/s in a direction 45 degrees SE relative to
the ground.
Find the resultant velocity of the airplane relative to the ground.

31. Projectile Motion
Vx
When we drop a ball
from a height we know
Vy
that its speed increases
as it falls.
y
The increase in speed is
due to the acceleration
gravity, g = 9.8 m/sec2.
x

32. Horizontal Speed
The ball’s horizontal velocity
remains constant while it falls
because gravity does not exert
any horizontal force.
Since there is no force, the
horizontal acceleration is zero
(ax = 0).
The ball will keep moving to
the right at 5 m/sec.

33. Horizontal Speed
The horizontal distance a projectile moves can
be calculated according to the formula:

34. Vertical Speed
The vertical speed (vy) of the
ball will increase by 9.8 m/sec
after each second.
After one second has passed, vy
of the ball will be 9.8 m/sec.
After the 2nd second has
passed, vy will be 19.6 m/sec
and so on.

36. Calculate using projectile motion
A stunt driver steers a car off
a cliff at a speed of 20
meters per second.
He lands in the lake below
two seconds later.
Find the height of the cliff and
the horizontal distance the car
travels.

37. Projectiles Launched at an Angle
A soccer ball kicked
off the ground is also
a projectile, but it
starts with an initial
velocity that has both
vertical and
horizontal
components.
*The launch angle determines how the initial velocity divides
between vertical (y) and horizontal (x) directions.

38. Steep Angle
A ball launched at
a steep angle will
have a large
vertical velocity
component and a
small horizontal
velocity.

39. Shallow Angle
A ball launched at a
low angle will have
a large horizontal
velocity component
and a small vertical
one.

40. Projectiles Launched at an Angle
The initial velocity components of an object launched at a velocity vo and
angle θ are found by breaking the velocity into x and y components.

41. Range of a Projectile
The range, or horizontal distance, traveled by a projectile
depends on the launch speed and the launch angle.

42. Range of a Projectile
The range of a projectile is calculated from the
horizontal velocity and the time of flight.

43. Range of a Projectile
A projectile travels farthest when launched at 45
degrees.

44. Range of a Projectile
The vertical velocity is responsible for giving the
projectile its "hang" time.

45. Hang Time
You can easily calculate your own hang time.
Run toward a doorway and jump as high as you can, touching
the wall or door frame.
Have someone watch to see exactly how high you reach.
Measure this distance with a meter stick.
The vertical distance formula can be rearranged to solve for
time:

46. Projectile Motion and the Velocity Vector
Key Question:
Can you predict the landing spot of a projectile?

47. Marble’s Path
Vx
t=?
Vy
y
x=?

48. In order to solve “x” we must know “t”
Y = vot – ½ g t2
vot = 0 (zero)
Y = ½ g t2
2y = g t2 t2 = 2y t = 2y
g
g