Uploaded bygeethawilliam
PPTX, PDF4,128 views

Geometric transformation 2d chapter 5

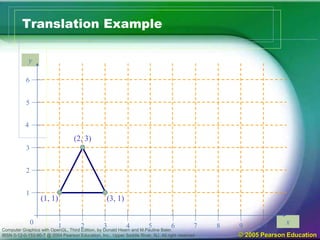
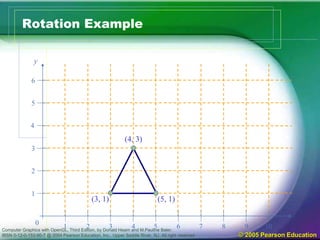
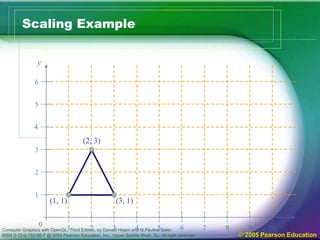
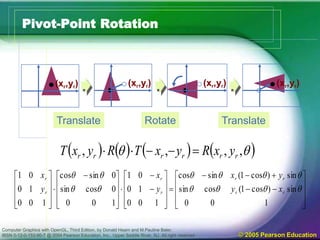
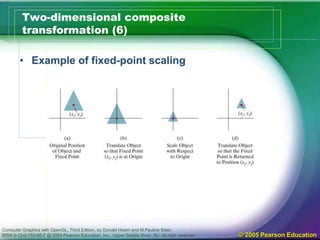
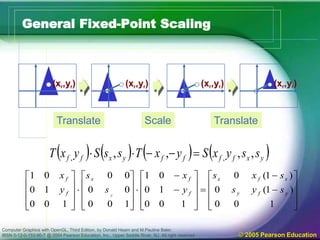
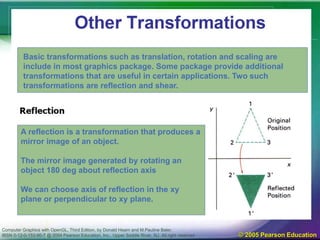
The document discusses various 2D geometric transformations including translation, rotation, and scaling. Translation moves objects by adding offsets to coordinates. Rotation changes the orientation of objects by specifying an axis and angle of rotation. Scaling alters the size of objects by multiplying coordinates by scaling factors. These transformations can be represented by 3x3 matrices using homogeneous coordinates, allowing multiple transformations to be combined through matrix multiplication.

Education◦
In this document
Powered by AI

Introduction to computer graphics, focusing on geometric transformations.

Basic transformations in computer graphics: translation, scaling, and rotation with purposes.

How to translate objects in 2D, including adding offsets using matrix operations and translation examples.

Understanding 2D rotation by specifying the axis and angle, complete with an example.

Explanation of how scaling alters size through matrix operations, illustrated with a scaling example.

Introduction to homogeneous coordinates and their significance in simplifying transformations.

Inverse operations for translation, rotation, and scaling matrices in two-dimensional spaces.

Discussion on defining composite transformations through a series of translations, rotations, and scalings.

Details on pivot-point rotation methods and their representation with matrix operations.

Process of fixed-point scaling through translating, scaling, and returning to original position.

General scaling directions and transformed shapes illustrated with matrix representations.

Overview of additional transformations such as reflection and shear in computer graphics.

Embed presentation

Downloaded 387 times
© 2005 Pearson Education Computer Graphics
© 2005 Pearson Education Chapter 5 Geometric Transformations
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Geometric Transformations • Basic transformations: – Translation – Scaling – Rotation • Purposes: – To move the position of objects – To alter the shape / size of objects – To change the orientation of objects
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Basic two-dimensional geometric transformations (1/1) • Two-Dimensional translation – One of rigid-body transformation, which move objects without deformation – Translate an object by Adding offsets to coordinates to generate new coordinates positions – Set tx,ty be the translation distance, we have – In matrix format, where T is the translation vector xtx'x  yty'y         y x P        y x t t T       'y 'x 'P TP'P 
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education – We could translate an object by applying the equation to every point of an object. • Because each line in an object is made up of an infinite set of points, however, this process would take an infinitely long time. • Fortunately we can translate all the points on a line by translating only the line’s endpoints and drawing a new line between the endpoints. • This figure translates the “house” by (3, -4) Basic two-dimensional geometric transformations (1/2)
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Translation Example y x0 1 1 2 2 3 4 5 6 7 8 9 10 3 4 5 6 (1, 1) (3, 1) (2, 3)
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Basic two-dimensional geometric transformations (2/1) • Two-Dimensional rotation – Rotation axis and angle are specified for rotation – Convert coordinates into polar form for calculation – Example, to rotation an object with angle a • The new position coordinates • In matrix format • Rotation about a point (xr, yr) cosrx  sinry            cossin sincos R PR'P    cossincossinsincos)sin(' sincossinsincoscos)cos(' yxrrry yxrrrx     cos)(sin)(' sin)(cos)(' rrr rrr yyxxyy yyxxxx   r r
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education – This figure shows the rotation of the house by 45 degrees. • Positive angles are measured counterclockwise (from x towards y) • For negative angles, you can use the identities: – cos(-) = cos() and sin(-)=-sin() Basic two-dimensional geometric transformations (2/2) 6    y x0 1 1 2 2 3 4 5 6 7 8 9 10 3 4 5 6
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Rotation Example y 0 1 1 2 2 3 4 5 6 7 8 9 10 3 4 5 6 (3, 1) (5, 1) (4, 3)
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Basic two-dimensional geometric transformations (3/1) • Two-Dimensional scaling – To alter the size of an object by multiplying the coordinates with scaling factor sx and sy – In matrix format, where S is a 2by2 scaling matrix – Choosing a fix point (xf, yf) as its centroid to perform scaling xsx'x  ysyy                    y x s0 0s 'y 'x y x PS'P  )s1(ysy'y )s1(xsx'x yfy xfx  
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education – In this figure, the house is scaled by 1/2 in x and 1/4 in y • Notice that the scaling is about the origin: – The house is smaller and closer to the origin Basic two-dimensional geometric transformations (3/2)
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Scaling Note: House shifts position relative to origin y x 0 1 1 2 2 3 4 5 6 7 8 9 10 3 4 5 6       1 2       1 3       3 6       3 9 – If the scale factor had been greater than 1, it would be larger and farther away. WATCH OUT: Objects grow and move!
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Scaling Example y 0 1 1 2 2 3 4 5 6 7 8 9 10 3 4 5 6 (1, 1) (3, 1) (2, 3)
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Homogeneous Coordinates • A point (x, y) can be re-written in homogeneous coordinates as (xh, yh, h) • The homogeneous parameter h is a non- zero value such that: • We can then write any point (x, y) as (hx, hy, h) • We can conveniently choose h = 1 so that (x, y) becomes (x, y, 1) h x x h  h y y h 
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Why Homogeneous Coordinates? • Mathematicians commonly use homogeneous coordinates as they allow scaling factors to be removed from equations • We will see in a moment that all of the transformations we discussed previously can be represented as 3*3 matrices • Using homogeneous coordinates allows us use matrix multiplication to calculate transformations – extremely efficient!
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Homogenous Coordinates • Combine the geometric transformation into a single matrix with 3by3 matrices • Expand each 2D coordinate to 3D coordinate with homogenous parameter • Two-Dimensional translation matrix • Two-Dimensional rotation matrix • Two-Dimensional scaling matrix                                 1 y x 100 t10 t01 1 'y 'x y x                                  1 y x 100 0cossin 0coscos 1 'y 'x                                   1 y x 100 0s0 00s 1 'y 'x y x
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Inverse transformations • Inverse translation matrix • Two-Dimensional translation matrix • Two-Dimensional translation matrix              100 t10 t01 T y x 1            100 0cossin 0sincos R 1                      100 0 s 1 0 00 s 1 S x x 1
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Two-dimensional composite transformation (1) • Composite transformation – A sequence of transformations – Calculate composite transformation matrix rather than applying individual transformations • Composite two-dimensional translations – Apply two successive translations, T1 and T2 – Composite transformation matrix in coordinate form PM'P PMM'P 12   PTTPTTP ttTT ttTT yx yx    )()(' ),( ),( 1212 222 111 ),(),(),( 21211122 yyxxyxyx ttttTttTttT 
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Two-dimensional composite transformation (2) • Composite two-dimensional rotations – Two successive rotations, R1 and R2 into a point P – Multiply two rotation matrices to get composite transformation matrix • Composite two-dimensional scaling PRRP PRRP   )}()({' })({)(' 12 12   PssssSP ssssSssSssS yyxx yyxxyxyx   ),(' ),(),(),( 2121 21212211 PRP RRR   )(' )()()( 21 2112  
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Two-dimensional composite transformation (3) • General two-dimensional Pivot-point rotation – Graphics package provide only origin rotation – Perform a translate-rotate-translate sequence • Translate the object to move pivot-point position to origin • Rotate the object • Translate the object back to the original position – Composite matrix in coordinates form ),y,x(R)y,x(T)(R)y,x(T rrrrrr  
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Two-dimensional composite transformation (4) • Example of pivot-point rotation
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Pivot-Point Rotation                                                 100 sin)cos1(cossin sin)cos1(sincos 100 10 01 100 0cossin 0sincos 100 10 01     rr rr r r r r xy yx y x y x         ,,,, rrrrrr yxRyxTRyxT  Translate Rotate Translate (xr,yr) (xr,yr) (xr,yr)(xr,yr)
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Two-dimensional composite transformation (5) • General two-dimensional Fixed-point scaling – Perform a translate-scaling-translate sequence • Translate the object to move fixed-point position to origin • Scale the object wrt. the coordinate origin • Use inverse of translation in step 1 to return the object back to the original position – Composite matrix in coordinates form )s,s,y,x(S)y,x(T)s,s(S)y,x(T yxffffyxff 
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Two-dimensional composite transformation (6) • Example of fixed-point scaling
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education General Fixed-Point Scaling                                                100 )1(0 )1(0 100 10 01 100 00 00 100 10 01 yfy xfx f fx f f sys sxs y x s s y x y Translate Scale Translate (xr,yr) (xr,yr) (xr,yr) (xr,yr)        yxffffyxff ssyxSyxTssSyxT ,,,, ,, 
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Two-dimensional composite transformation (7) • General two-dimensional scaling directions – Perform a rotate-scaling-rotate sequence – Composite matrix in coordinates form               100 0cosssinssincos)ss( 0sincos)ss(sinscoss )(R)s,s(S)(R 2 2 2 112 12 2 2 2 1 21 1     s1 s2
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education General Scaling Directions • Converted to a parallelogram              100 0cossinsincos)( 0sincos)(sincos )(),()( 2 2 2 112 12 2 2 2 1 21 1    ssss ssss RssSR x y (0,0) (3/2,1/2) (1/2,3/2) (2,2) x y (0,0) (1,0) (0,1) (1,1) x y s 2 s 1  Scale
Computer Graphics with OpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Basic transformations such as translation, rotation and scaling are include in most graphics package. Some package provide additional transformations that are useful in certain applications. Two such transformations are reflection and shear. A reflection is a transformation that produces a mirror image of an object. The mirror image generated by rotating an object 180 deg about reflection axis We can choose axis of reflection in the xy plane or perpendicular to xy plane.

More Related Content

PPTX
polygon clipping IN COMPUTER GRAPHICS.pptx
byurvashipundir04
 
PPT
COMPOSITE TRANSFORMATION COMPUTER GRAPHICDS.ppt
byurvashipundir04
 
PPT
Two dimensional geometric transformations
byMohammad Sadiq
 
PDF
3D Transformation
bySwatiHans10
 
PPTX
3 d display methods
byShami Al Rahad
 
PPT
Computer graphics iv unit
byaravindangc
 
PPT
hidden surface elimination using z buffer algorithm
byrajivagarwal23dei
 
PPT
Raster scan system
byMohd Arif
 
polygon clipping IN COMPUTER GRAPHICS.pptx
byurvashipundir04
 
COMPOSITE TRANSFORMATION COMPUTER GRAPHICDS.ppt
byurvashipundir04
 
Two dimensional geometric transformations
byMohammad Sadiq
 
3D Transformation
bySwatiHans10
 
3 d display methods
byShami Al Rahad
 
Computer graphics iv unit
byaravindangc
 
hidden surface elimination using z buffer algorithm
byrajivagarwal23dei
 
Raster scan system
byMohd Arif
 

What's hot

PPTX
Video display devices
byshalinikarunakaran1
 
PDF
Computer graphics notes
bysmruti sarangi
 
PPT
Polygon clipping
byMohd Arif
 
PDF
4. THREE DIMENSIONAL DISPLAY METHODS
bySanthiNivas
 
PDF
Unit-IV Windowing and Clipping.pdf
byAmol Gaikwad
 
PDF
2D Transformation in Computer Graphics
byA. S. M. Shafi
 
PPTX
Computer graphics
byNanhen Verma
 
PPTX
Image enhancement lecture
byISRAR HUSSAIN
 
PPTX
Mid point line Algorithm - Computer Graphics
byDrishti Bhalla
 
PPT
Window to viewport transformation
byAnkit Garg
 
PPTX
Computer Graphics - Windowing and Clipping
byDr. Chandrakant Divate
 
PPTX
Cohen-Sutherland Line Clipping Algorithm
byMaruf Abdullah (Rion)
 
PPTX
KEY FRAME SYSTEM-Ruby Stella mary.pptx
byComputerScienceDepar6
 
PPT
Visible Surface Detection
byAmitBiswas99
 
PPTX
3D Graphics : Computer Graphics Fundamentals
byMuhammed Afsal Villan
 
PPTX
3d transformation computer graphics
byUniversity of Potsdam
 
PPTX
Back face detection
byPooja Dixit
 
PPTX
Hidden surface removal algorithm
byKKARUNKARTHIK
 
PPTX
COMPUTER GRAPHICS-"Projection"
byAnkit Surti
 
PPTX
BRESENHAM’S LINE DRAWING ALGORITHM
bySt Mary's College,Thrissur,Kerala
 
Video display devices
byshalinikarunakaran1
 
Computer graphics notes
bysmruti sarangi
 
Polygon clipping
byMohd Arif
 
4. THREE DIMENSIONAL DISPLAY METHODS
bySanthiNivas
 
Unit-IV Windowing and Clipping.pdf
byAmol Gaikwad
 
2D Transformation in Computer Graphics
byA. S. M. Shafi
 
Computer graphics
byNanhen Verma
 
Image enhancement lecture
byISRAR HUSSAIN
 
Mid point line Algorithm - Computer Graphics
byDrishti Bhalla
 
Window to viewport transformation
byAnkit Garg
 
Computer Graphics - Windowing and Clipping
byDr. Chandrakant Divate
 
Cohen-Sutherland Line Clipping Algorithm
byMaruf Abdullah (Rion)
 
KEY FRAME SYSTEM-Ruby Stella mary.pptx
byComputerScienceDepar6
 
Visible Surface Detection
byAmitBiswas99
 
3D Graphics : Computer Graphics Fundamentals
byMuhammed Afsal Villan
 
3d transformation computer graphics
byUniversity of Potsdam
 
Back face detection
byPooja Dixit
 
Hidden surface removal algorithm
byKKARUNKARTHIK
 
COMPUTER GRAPHICS-"Projection"
byAnkit Surti
 
BRESENHAM’S LINE DRAWING ALGORITHM
bySt Mary's College,Thrissur,Kerala
 

Similar to Geometric transformation 2d chapter 5

PPTX
Part 2- Geometric Transformation.pptx
byKhalil Alhatab
 
PPT
Two dimentional transform
byPatel Punit
 
PPTX
Part 2- Transformation.pptx
byKhalil Alhatab
 
PDF
2D Transformation.pdf
bymaheshshinde762539
 
PPT
2D_transformatiomcomputer graphics 2d translation, rotation and scaling trans...
byrenuka b
 
PPTX
Transformations computer graphics
byVikram Halder
 
PPTX
Computer Graphics Unit 2
byaravindangc
 
PPT
Cs8092 computer graphics and multimedia unit 2
bySIMONTHOMAS S
 
PDF
Computer Graphics & linear Algebra
byXad Kuain
 
PPTX
Part 3- Manipulation and Representation of Curves.pptx
byKhalil Alhatab
 
PPT
2D-Transformations-Transformations are the operations applied to geometrical ...
byBINJAD1
 
PPT
lecture-9-online WORK PART UNIFORMITY IN
bysailavanyar1
 
PPTX
Lecture 6-1543909797
byCanh Le
 
PPTX
lecture11-11_16827_2d-transformations in computer graphics
bylarytonex
 
PDF
3. Geometric Transformation (2D) Computer Graphics.pdf
byu20mcse011p
 
PPTX
2D and 3D Geometric transformations.pptx
bysindhupriya344409
 
PPTX
Computer Graphics Three-Dimensional Geometric Transformations
byDr. Chandrakant Divate
 
PPTX
Three dimensional geometric transformations
byshanthishyam
 
PPT
transformation in open GL. why use open GL modes
byjawadsafee
 
PPT
2D_Transformations in computer graphicsCG
byPriyankaPatil919748
 
Part 2- Geometric Transformation.pptx
byKhalil Alhatab
 
Two dimentional transform
byPatel Punit
 
Part 2- Transformation.pptx
byKhalil Alhatab
 
2D Transformation.pdf
bymaheshshinde762539
 
2D_transformatiomcomputer graphics 2d translation, rotation and scaling trans...
byrenuka b
 
Transformations computer graphics
byVikram Halder
 
Computer Graphics Unit 2
byaravindangc
 
Cs8092 computer graphics and multimedia unit 2
bySIMONTHOMAS S
 
Computer Graphics & linear Algebra
byXad Kuain
 
Part 3- Manipulation and Representation of Curves.pptx
byKhalil Alhatab
 
2D-Transformations-Transformations are the operations applied to geometrical ...
byBINJAD1
 
lecture-9-online WORK PART UNIFORMITY IN
bysailavanyar1
 
Lecture 6-1543909797
byCanh Le
 
lecture11-11_16827_2d-transformations in computer graphics
bylarytonex
 
3. Geometric Transformation (2D) Computer Graphics.pdf
byu20mcse011p
 
2D and 3D Geometric transformations.pptx
bysindhupriya344409
 
Computer Graphics Three-Dimensional Geometric Transformations
byDr. Chandrakant Divate
 
Three dimensional geometric transformations
byshanthishyam
 
transformation in open GL. why use open GL modes
byjawadsafee
 
2D_Transformations in computer graphicsCG
byPriyankaPatil919748
 

Recently uploaded

PDF
Most Imp Chapters & Weightage for Boards 2025.pdf
byTamannaSagar
 
PPTX
Multiple Linear Regression - Least Square Method X₁ on X₂ and X₃
bySundar B N
 
PPTX
10-12-2025 Francois Staring How can Researchers and Initial Teacher Educators...
byEduSkills OECD
 
PDF
Multiple Myeloma , definition, etiology, PP, CM , DE and management
byNisha Borsa
 
PPTX
TAMIS & TEMS - HOW, WHY and THE STEPS IN PROCTOLOGY
byJohn Thanakumar
 
PPTX
How to Configure Push & Pull Rule in Odoo 18 Inventory
byCeline George
 
PDF
Using Charts and Tables in Presenting Data
byThelma Villaflores
 
PPTX
Semester 6 Unit 2 Club foot (talipes).pptx
bysachin7989
 
PPTX
Basics in Phytochemistry, Extraction, Isolation methods, Characterisation etc.
byD. Y. Patil College of Pharmacy, Kolhapur.
 
PPTX
How to Manage Package Reservation in Odoo 18 Inventory
byCeline George
 
PPTX
Nursing Unit Management, patient care unit, physical layout of nursing unit,t...
byyellow4878
 
PPTX
Steve Hale - Developing Elite Young Goalkeepers 2024.pptx
bypjmfd
 
PPTX
PURPOSIVE SAMPLING IN EDUCATIONAL RESEARCH RACHITHRA RK.pptx
byssuser047b711
 
PDF
The voice of the rain poem class 11th.pdf
byReeta Baral
 
PDF
International Men's Day Event: Breaking the Silence: Embracing Vulnerability ...
byAssociation for Project Management
 
PPTX
Access partner report in Odoo 18.2 _ Odoo 19
byCeline George
 
PPTX
Growth & Development MILESTONES (ADOLESCENTS ).pptx
byAneetaSharma15
 
PDF
Types of eggs and Egg membranes (Developmental Zoology)
bySudhandraKarthi
 
PPTX
PARENTAL ROUTES OF DRUGS ADMINISTRATION .pptx
byAneetaSharma15
 
PPTX
4 G8_Q3_L4 (Evaluating opinion editorials for textual evidence and quality).pptx
byNorafeSahagun
 
Most Imp Chapters & Weightage for Boards 2025.pdf
byTamannaSagar
 
Multiple Linear Regression - Least Square Method X₁ on X₂ and X₃
bySundar B N
 
10-12-2025 Francois Staring How can Researchers and Initial Teacher Educators...
byEduSkills OECD
 
Multiple Myeloma , definition, etiology, PP, CM , DE and management
byNisha Borsa
 
TAMIS & TEMS - HOW, WHY and THE STEPS IN PROCTOLOGY
byJohn Thanakumar
 
How to Configure Push & Pull Rule in Odoo 18 Inventory
byCeline George
 
Using Charts and Tables in Presenting Data
byThelma Villaflores
 
Semester 6 Unit 2 Club foot (talipes).pptx
bysachin7989
 
Basics in Phytochemistry, Extraction, Isolation methods, Characterisation etc.
byD. Y. Patil College of Pharmacy, Kolhapur.
 
How to Manage Package Reservation in Odoo 18 Inventory
byCeline George
 
Nursing Unit Management, patient care unit, physical layout of nursing unit,t...
byyellow4878
 
Steve Hale - Developing Elite Young Goalkeepers 2024.pptx
bypjmfd
 
PURPOSIVE SAMPLING IN EDUCATIONAL RESEARCH RACHITHRA RK.pptx
byssuser047b711
 
The voice of the rain poem class 11th.pdf
byReeta Baral
 
International Men's Day Event: Breaking the Silence: Embracing Vulnerability ...
byAssociation for Project Management
 
Access partner report in Odoo 18.2 _ Odoo 19
byCeline George
 
Growth & Development MILESTONES (ADOLESCENTS ).pptx
byAneetaSharma15
 
Types of eggs and Egg membranes (Developmental Zoology)
bySudhandraKarthi
 
PARENTAL ROUTES OF DRUGS ADMINISTRATION .pptx
byAneetaSharma15
 
4 G8_Q3_L4 (Evaluating opinion editorials for textual evidence and quality).pptx
byNorafeSahagun
 

Geometric transformation 2d chapter 5

  • 1.
    © 2005 PearsonEducation Computer Graphics
  • 2.
    © 2005 PearsonEducation Chapter 5 Geometric Transformations
  • 3.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Geometric Transformations • Basic transformations: – Translation – Scaling – Rotation • Purposes: – To move the position of objects – To alter the shape / size of objects – To change the orientation of objects
  • 4.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Basic two-dimensional geometric transformations (1/1) • Two-Dimensional translation – One of rigid-body transformation, which move objects without deformation – Translate an object by Adding offsets to coordinates to generate new coordinates positions – Set tx,ty be the translation distance, we have – In matrix format, where T is the translation vector xtx'x  yty'y         y x P        y x t t T       'y 'x 'P TP'P 
  • 5.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education – We could translate an object by applying the equation to every point of an object. • Because each line in an object is made up of an infinite set of points, however, this process would take an infinitely long time. • Fortunately we can translate all the points on a line by translating only the line’s endpoints and drawing a new line between the endpoints. • This figure translates the “house” by (3, -4) Basic two-dimensional geometric transformations (1/2)
  • 6.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Translation Example y x0 1 1 2 2 3 4 5 6 7 8 9 10 3 4 5 6 (1, 1) (3, 1) (2, 3)
  • 7.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Basic two-dimensional geometric transformations (2/1) • Two-Dimensional rotation – Rotation axis and angle are specified for rotation – Convert coordinates into polar form for calculation – Example, to rotation an object with angle a • The new position coordinates • In matrix format • Rotation about a point (xr, yr) cosrx  sinry            cossin sincos R PR'P    cossincossinsincos)sin(' sincossinsincoscos)cos(' yxrrry yxrrrx     cos)(sin)(' sin)(cos)(' rrr rrr yyxxyy yyxxxx   r r
  • 8.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education – This figure shows the rotation of the house by 45 degrees. • Positive angles are measured counterclockwise (from x towards y) • For negative angles, you can use the identities: – cos(-) = cos() and sin(-)=-sin() Basic two-dimensional geometric transformations (2/2) 6    y x0 1 1 2 2 3 4 5 6 7 8 9 10 3 4 5 6
  • 9.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Rotation Example y 0 1 1 2 2 3 4 5 6 7 8 9 10 3 4 5 6 (3, 1) (5, 1) (4, 3)
  • 10.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Basic two-dimensional geometric transformations (3/1) • Two-Dimensional scaling – To alter the size of an object by multiplying the coordinates with scaling factor sx and sy – In matrix format, where S is a 2by2 scaling matrix – Choosing a fix point (xf, yf) as its centroid to perform scaling xsx'x  ysyy                    y x s0 0s 'y 'x y x PS'P  )s1(ysy'y )s1(xsx'x yfy xfx  
  • 11.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education – In this figure, the house is scaled by 1/2 in x and 1/4 in y • Notice that the scaling is about the origin: – The house is smaller and closer to the origin Basic two-dimensional geometric transformations (3/2)
  • 12.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Scaling Note: House shifts position relative to origin y x 0 1 1 2 2 3 4 5 6 7 8 9 10 3 4 5 6       1 2       1 3       3 6       3 9 – If the scale factor had been greater than 1, it would be larger and farther away. WATCH OUT: Objects grow and move!
  • 13.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Scaling Example y 0 1 1 2 2 3 4 5 6 7 8 9 10 3 4 5 6 (1, 1) (3, 1) (2, 3)
  • 14.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Homogeneous Coordinates • A point (x, y) can be re-written in homogeneous coordinates as (xh, yh, h) • The homogeneous parameter h is a non- zero value such that: • We can then write any point (x, y) as (hx, hy, h) • We can conveniently choose h = 1 so that (x, y) becomes (x, y, 1) h x x h  h y y h 
  • 15.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Why Homogeneous Coordinates? • Mathematicians commonly use homogeneous coordinates as they allow scaling factors to be removed from equations • We will see in a moment that all of the transformations we discussed previously can be represented as 3*3 matrices • Using homogeneous coordinates allows us use matrix multiplication to calculate transformations – extremely efficient!
  • 16.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Homogenous Coordinates • Combine the geometric transformation into a single matrix with 3by3 matrices • Expand each 2D coordinate to 3D coordinate with homogenous parameter • Two-Dimensional translation matrix • Two-Dimensional rotation matrix • Two-Dimensional scaling matrix                                 1 y x 100 t10 t01 1 'y 'x y x                                  1 y x 100 0cossin 0coscos 1 'y 'x                                   1 y x 100 0s0 00s 1 'y 'x y x
  • 17.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Inverse transformations • Inverse translation matrix • Two-Dimensional translation matrix • Two-Dimensional translation matrix              100 t10 t01 T y x 1            100 0cossin 0sincos R 1                      100 0 s 1 0 00 s 1 S x x 1
  • 18.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Two-dimensional composite transformation (1) • Composite transformation – A sequence of transformations – Calculate composite transformation matrix rather than applying individual transformations • Composite two-dimensional translations – Apply two successive translations, T1 and T2 – Composite transformation matrix in coordinate form PM'P PMM'P 12   PTTPTTP ttTT ttTT yx yx    )()(' ),( ),( 1212 222 111 ),(),(),( 21211122 yyxxyxyx ttttTttTttT 
  • 19.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Two-dimensional composite transformation (2) • Composite two-dimensional rotations – Two successive rotations, R1 and R2 into a point P – Multiply two rotation matrices to get composite transformation matrix • Composite two-dimensional scaling PRRP PRRP   )}()({' })({)(' 12 12   PssssSP ssssSssSssS yyxx yyxxyxyx   ),(' ),(),(),( 2121 21212211 PRP RRR   )(' )()()( 21 2112  
  • 20.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Two-dimensional composite transformation (3) • General two-dimensional Pivot-point rotation – Graphics package provide only origin rotation – Perform a translate-rotate-translate sequence • Translate the object to move pivot-point position to origin • Rotate the object • Translate the object back to the original position – Composite matrix in coordinates form ),y,x(R)y,x(T)(R)y,x(T rrrrrr  
  • 21.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Two-dimensional composite transformation (4) • Example of pivot-point rotation
  • 22.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Pivot-Point Rotation                                                 100 sin)cos1(cossin sin)cos1(sincos 100 10 01 100 0cossin 0sincos 100 10 01     rr rr r r r r xy yx y x y x         ,,,, rrrrrr yxRyxTRyxT  Translate Rotate Translate (xr,yr) (xr,yr) (xr,yr)(xr,yr)
  • 23.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Two-dimensional composite transformation (5) • General two-dimensional Fixed-point scaling – Perform a translate-scaling-translate sequence • Translate the object to move fixed-point position to origin • Scale the object wrt. the coordinate origin • Use inverse of translation in step 1 to return the object back to the original position – Composite matrix in coordinates form )s,s,y,x(S)y,x(T)s,s(S)y,x(T yxffffyxff 
  • 24.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Two-dimensional composite transformation (6) • Example of fixed-point scaling
  • 25.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education General Fixed-Point Scaling                                                100 )1(0 )1(0 100 10 01 100 00 00 100 10 01 yfy xfx f fx f f sys sxs y x s s y x y Translate Scale Translate (xr,yr) (xr,yr) (xr,yr) (xr,yr)        yxffffyxff ssyxSyxTssSyxT ,,,, ,, 
  • 26.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Two-dimensional composite transformation (7) • General two-dimensional scaling directions – Perform a rotate-scaling-rotate sequence – Composite matrix in coordinates form               100 0cosssinssincos)ss( 0sincos)ss(sinscoss )(R)s,s(S)(R 2 2 2 112 12 2 2 2 1 21 1     s1 s2
  • 27.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education General Scaling Directions • Converted to a parallelogram              100 0cossinsincos)( 0sincos)(sincos )(),()( 2 2 2 112 12 2 2 2 1 21 1    ssss ssss RssSR x y (0,0) (3/2,1/2) (1/2,3/2) (2,2) x y (0,0) (1,0) (0,1) (1,1) x y s 2 s 1  Scale
  • 28.
    Computer Graphics withOpenGL, Third Edition, by Donald Hearn and M.Pauline Baler. IBSN 0-12-0-153-90-7 @ 2004 Pearson Education, Inc., Upper Saddle River, NJ. All right reserved © 2005 Pearson Education Basic transformations such as translation, rotation and scaling are include in most graphics package. Some package provide additional transformations that are useful in certain applications. Two such transformations are reflection and shear. A reflection is a transformation that produces a mirror image of an object. The mirror image generated by rotating an object 180 deg about reflection axis We can choose axis of reflection in the xy plane or perpendicular to xy plane.