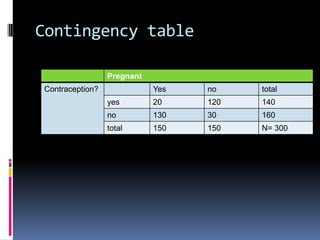
Non-parametric tests are used when data is not normally distributed. They analyze rankings of raw scores rather than means. The Mann-Whitney and Wilcoxon rank-sum tests compare two independent groups and are equivalent to a t-test. They ignore groupings and rank all data points, expecting similar ranks between groups if they are the same. The Kruskal-Wallis test compares multiple groups and is akin to an ANOVA. Chi square examines relationships between categorical variables by comparing observed and expected frequencies in a contingency table to determine if differences are due to chance.

1. Non-Parametric Tests Ryan Sain, Ph.D

2. Non-parametric tests These are used in the place of parametric stats When your data is not normal There are specific adjustments and procedures to not be affected by this Typically do not use the mean to make comparisons Most create rankings of the raw scores then analyze these rankings

3. Independent samples Comparing two groups of independent samples Equivalent to the t-test Mann-Whitney Wilcoxon rank-sum

4. Rank logic Ignoring the specific groups We rank all data from lowest (1st) to highest (nth) If the groups are the same you would expect similar ranks in each group The sums of these ranks will likely be similar if no difference between groups exist If the groups ARE different – then you will expect a disproportionate set of ranks in one group compared to the other and the sums of those ranks would be different. Same raw scores get an average of the ranks (tied ranks).

5. Standardizing and significance We can calculate a mean using n for each group: Wmean= n1(n1+n2+1)/2 SEWmean= SQRT (n1n2(n1+n2+1))/12 But we still need to get a standard error convert raw to z Using the mean calculated from above Magical +/-1.96

6. Two related conditions Wilcoxon signed rank test Used when the data are related (repeated measures of the same individuals) Is the same as the dependent t-test Use a negative sign of the rank dropped for a given person between test 1 and 2. Drop all people that did not change.

7. Testing multiple groups Kruskal-Wallis Uses the same ranking logic as the mann-whiteney Is akin to an ANOVA Omnibus test as well. Post hoc tests of mann-whitney or Wilcoxon rank-sum.

8. Categorical Data Categorical data is data that fits into only one category Gender Pregnancy Voting We have looked at using categorical data for predicting something (point biserial correlation) but now we want to examine the relationship between these variable types

9. The logic There is no mean or median to work with The values are arbitrary All we can really look at are frequencies of occurrence

10. Chi square Two categorical variables Pregnant and contraception used. What is the chance that our observations are not due to chance? We cannot look at means, we can only look at frequencies – so we need to find the expected values

11. Contingency table

12. Expected distributions So we look at what is expected in each cell. (cannot use n/cells to get this) Because there is a different number of people in each condition. So we make an adjustment Row total x column total / n X2 = the sum of each (observed-expected)2/expected This statistic is then able to be looked up on a probability table. We can then decide if the distribution is expected or not. Degrees of freedom (row-1)(column-1)

13. A sample X2 = (20-70)2/70 + ….. X2 = 35.71 + 35.71 +31.25 + 31.25 X2 = 133.92 with 2 df

14. assumptions No repeated measures situations Expected frequencies should be greater than 5

15. conclusion If you have categorical data and you are wanting to see if the distributions are by chance – use the Chi Square analysis.