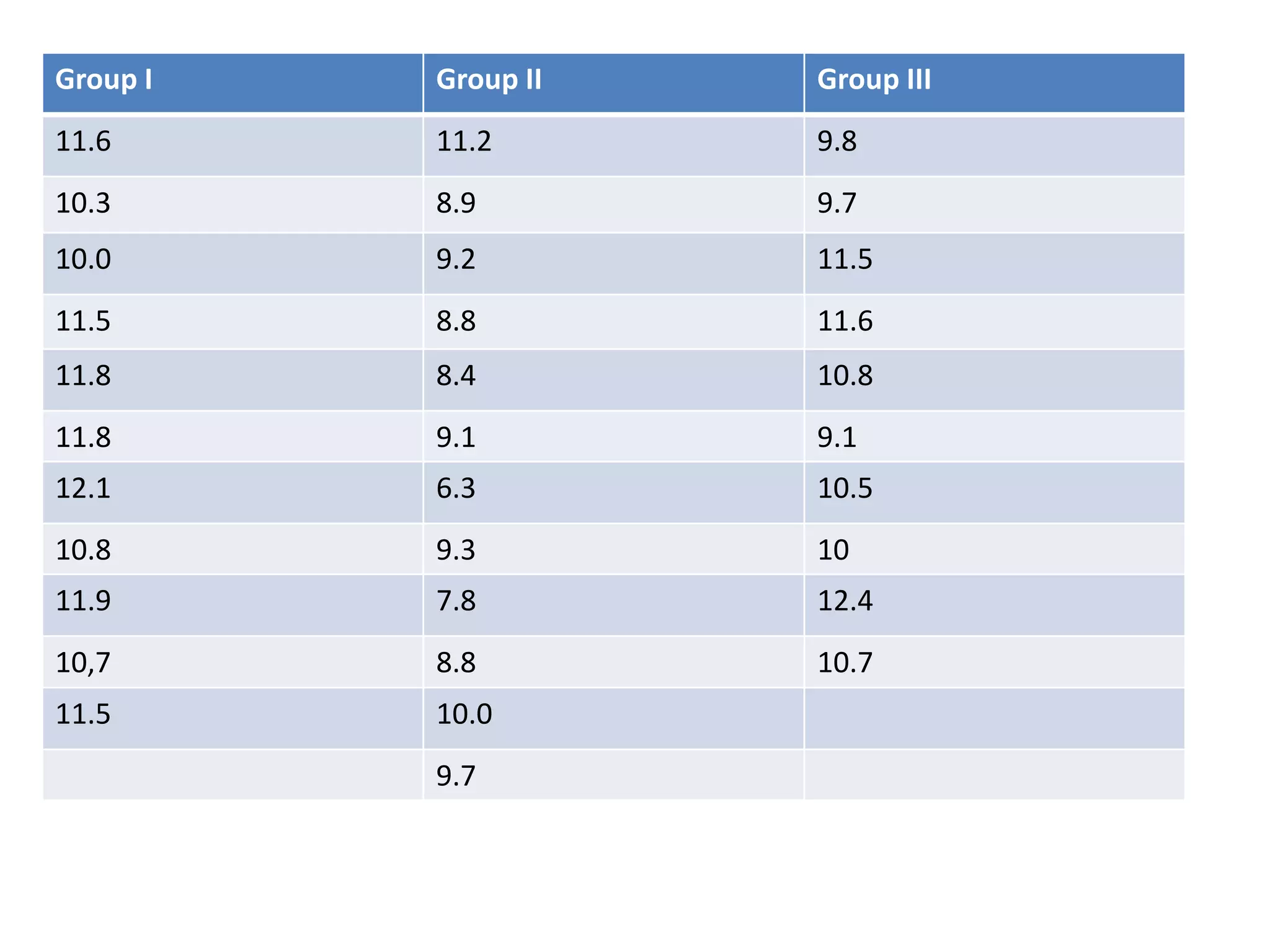
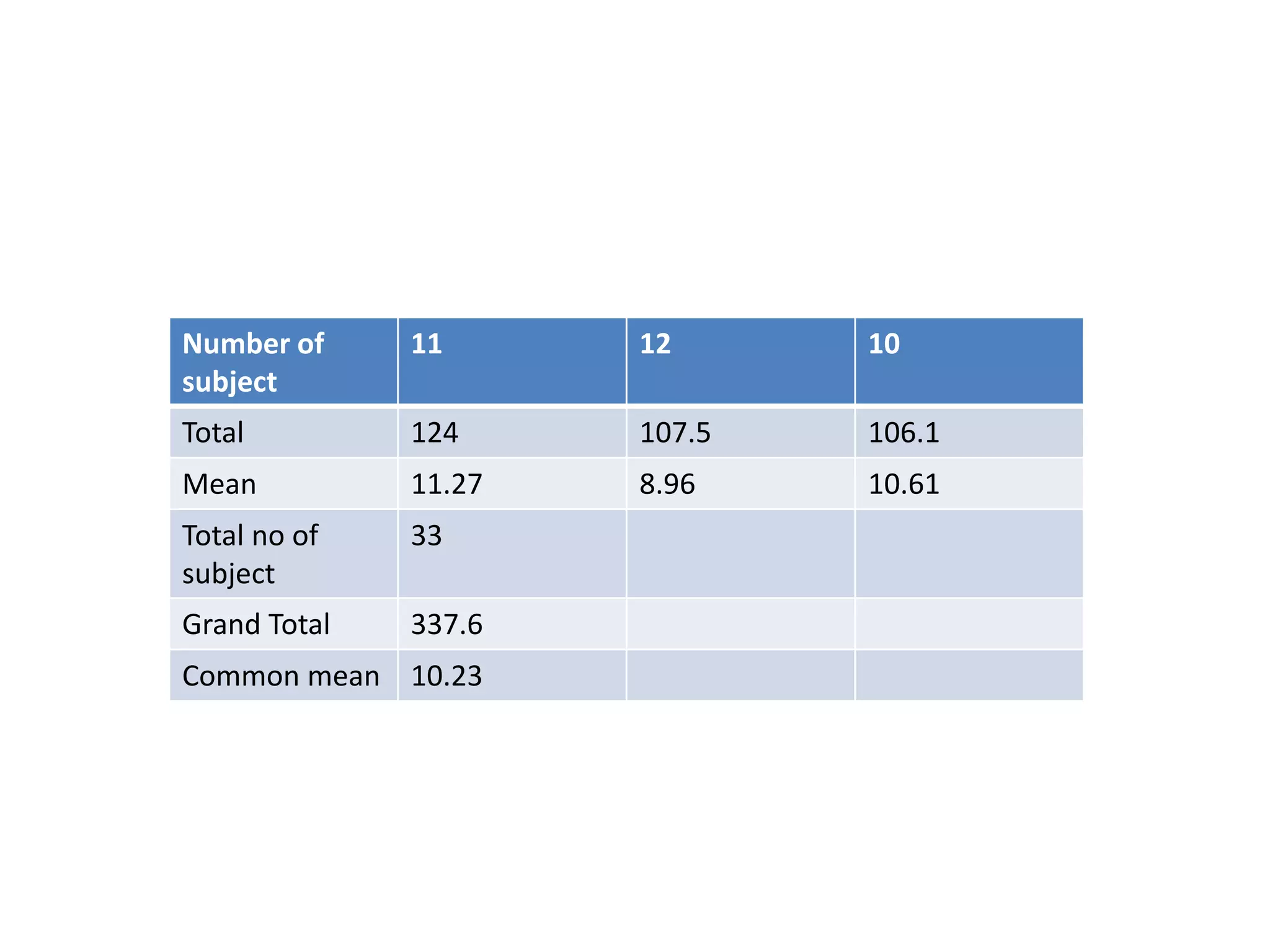
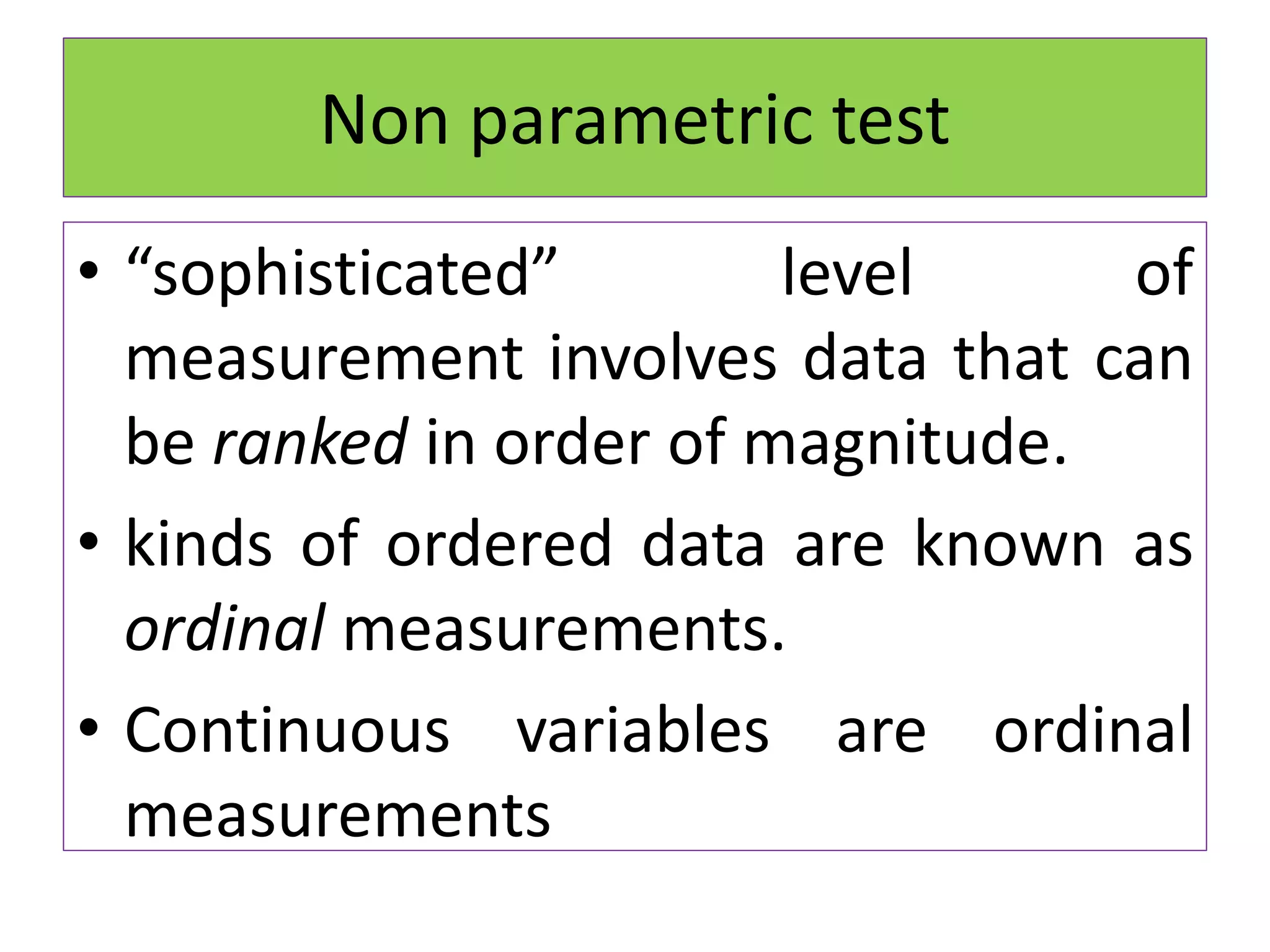
The document discusses non-parametric tests and provides information about when to use them. Non-parametric tests make fewer assumptions about the distribution of population values and can be used when sample sizes are small or the data is ordinal. Examples of non-parametric tests provided include the sign test, chi-square test, Mann-Whitney U test, and Kruskal-Wallis test. The general steps to perform a non-parametric test are also outlined.

1. Problem- ANOVA
The haemoglobin level of three
groups of children fed three
different diets are given in the
table. Test whether the means
of these groups differ
significantly

2. Group I Group II Group III
11.6 11.2 9.8
10.3 8.9 9.7
10.0 9.2 11.5
11.5 8.8 11.6
11.8 8.4 10.8
11.8 9.1 9.1
12.1 6.3 10.5
10.8 9.3 10
11.9 7.8 12.4
10,7 8.8 10.7
11.5 10.0
9.7

3. Number of
subject
11 12 10
Total 124 107.5 106.1
Mean 11.27 8.96 10.61
Total no of
subject
33
Grand Total 337.6
Common mean 10.23

4. Non Parametric test

5. Definition
It is the mathematical procedures
concerned with the treatment of
standard statistical problem.
when the assumption of normal are
replaced with general assumption for
the distribution function.

6. When to use non parametric test
• In experiments when the data is
not normal.
• Sample size is so small
• All the tests involving the ranking
of data are non parametric.

7. Nonparametric statistics, also known as
distribution-free statistics.
It may be applicable when the nature of
the distributions are unknown.
we are not willing to accept the
assumptions necessary for the application
of the usual statistical procedures.
When to use non parametric test

8. • some people believe that any kind of data, no
matter what the distribution, can be correctly
analyzed using nonparametric methods.
• Many believe that most nonparametric
methods require that the distributions be
• Continuous
• Symmetrical, and
• Independent
When to use non parametric test

9. Data that are categorical or attribute
measurements.
• These are also known as nominal
observations (i.e., the observation is
given a name).
• Thus, a person is observed to be a
“male” or a “female” or “black,”
“white,” or “yellow.”

10. The assignment of a number to such
nominal data may be useful to
differentiate the categories, perhaps
for computer usage.
For example, we could assign the
number 1 to a male and 2 to a female,
but this does not imply that a female is
larger (or, for that matter, smaller)
than a male.

11. Non parametric test
• “sophisticated” level of
measurement involves data that can
be ranked in order of magnitude.
• kinds of ordered data are known as
ordinal measurements.
• Continuous variables are ordinal
measurements

12. Ordinal measurement
• For example, patients receiving antidepressant
medication, may be rated according to attributes
such as “sociability.”
• A high score will be assigned to a patient
performing well on this criterion.
• If the patient shows characteristics of
“withdrawal,” a low score will result.
• Intermediary scores reflect various degrees of
response.
• These are ordinal measurements.

13. A patient with a score of zero after one
week of medication.
A score of 3 after two weeks of
medication can be said to have improved.
During the period between one and two
weeks of treatment.
A score of 3 is better than a score of zero.

14. Many nonparametric tests are based
on ranking data.
• The condition of the “depressed” patient is a
continuum.
• The condition can vary from one extreme to
another with infinitely small gradations, in
theory.
• It is not possible practically to measure the
subjective condition with its infinite subtleties,
and therefore we substitute an ordered scale that
approximates the condition of the patient.

15. • if a score of 3 represents “marked improvement”
in sociability, 2 represents “moderate
improvement,” and 1 represents “no
improvement,”
• one usually cannot say that the difference
between scores of 3 and 2 is equal in magnitude
to the difference of 2 and 1.
• Yet the data analysis of such scores usually treats
a difference between 3 and 2 as equivalent to a
difference between 2 and 1.

16. Data derived from continuous distributions are
particularly amenable to nonparametric
methods when the distributions deviate greatly
from normality.
A marked disadvantage of the simpler
nonparametric techniques is the lack of
flexibility of the design and analysis.
The sign test is probably the simplest of the
nonparametric tests.

17. • If the sample size is small [as 6] there is no
alternative to use a non parametric test unless
the nature of population distribution is
precisely known.
• Easy to learn
• It is applicable when the observation are
nominal, ordinal [ ranked ] , or measured
imprecisely
Advantage

18. • It is suitable for treating samples made
up of observations from different
populations.
• The hypothesis tested by the non
parametric test may be more appropriate
for the research investigation.
• It can be applied easier than parametric
tests.
Advantage

19. • It is used to modify the hypothesis rather than
estimation.
• Test is about the median instead of the mean.
• Tables of critical values may not be easily
available.
• Tests are not systematic.
Disadvantage

20. Some non parametric tests
When we have to test an assumption about the
population distribution with a random sample from
the population
• Binomial test- when data are in two categories
and the sample size is small.
• Chi- square test – when the data are in discrete
categories and the sample are sufficiently large.
• Kolmogorov – smirnov test – when the variable
has a continuous distribution

21. When we have to test if two random samples are
likely to have come from population with the same
mean.
Randomisation test- small samples when data
measurement in a numerical scale
Kolmogorov – smirnov test with weaker
measurement
Mann whitney U test- large samples when data
represent weaker measurement.
Median test
Some non parametric tests

22. Some non parametric tests
Kruskal – wallis test
When more than two sample are considered
when they all belong to same population.
Fisher exact probability test
It is used when scores from the independent
random samples all fall into one or other of
mutually exclusive classes.

23. Some non parametric tests
When we have to find out the statistical significance
of difference in matched pairs comparison.
Mecnemar test
Data are frequencies in different categories
Sign test
Data are on a variable with continuity but can be
measured only in a gross way.
Ranks within the pairs are used

24. Some non parametric tests
Wilcoxon test
• Differences observed for the various matched
pairs can be meaningfully ranked.
Randomisation test
• When data measurement in a numerical scale
and the sample size is sufficiently small

25. Some non parametric tests
When we have to measure the correlation as
the observations are ranked.
• Kendall’s tau
• Spearmann rho

26. Application
• When parametric tests are not
satisfied
• If testing hypothesis does not have
any distribution.
• In order to quickly analyse the data
• When unscaled data is available.

27. Assumptions
• Observations are independent
• Continuous variable
• It is applied appropriately to data
measured in an ordinal scale.

28. Test procedure- General steps to carry
out non parametric test
Stating hypothesis
• The null and alternative hypothesis is stated.
Setting significance level
• The alpha related significance level with null
hypothesis is set.
• it is normally set as 5% and therefore the
confidence level is 95 %

29. Selecting test
• Suitable statistic test is chosen
It is done by considering
• The number of sample,
• whether the sample is dependent or
independent.
• Types of data.
Calculating statistics
• The test statistics is then calculated.
• Comparing values
Test procedure- General steps to carry
out non parametric test

30. • The value required to reject the null hypothesis is
determined using the suitable table of critical
values for the specified statistics.
• This value is compared with the critical values
which enables us to find the difference based on
a specific significance level.
• Then we can state whether the null hypothesis
should be rejected or not.
Making decision
• The results are explained and a conclusion is
drawn.
Test procedure- General steps to carry
out non parametric test