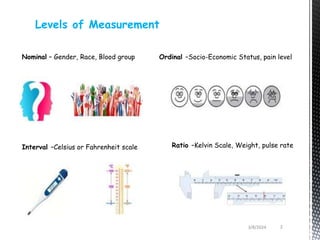
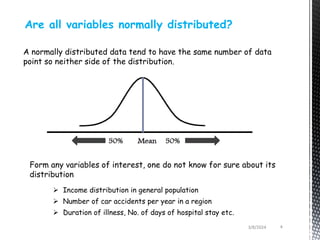
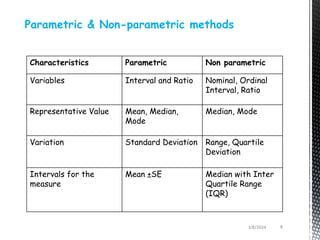
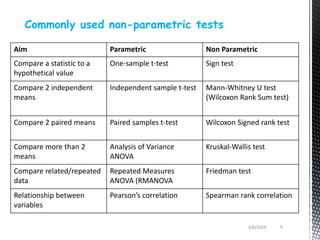
This document discusses parametric and non-parametric statistical methods. It defines different levels of measurement and provides examples of parametric and non-parametric tests. Key points include: - Parametric tests assume normal distributions and make inferences about population parameters, while non-parametric tests do not require assumptions about the distribution and can be used on ordinal or nominal data. 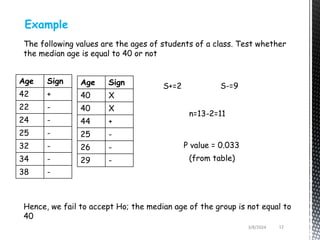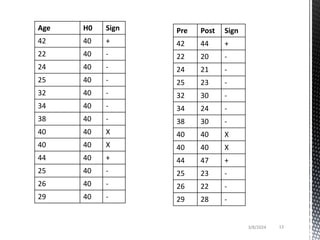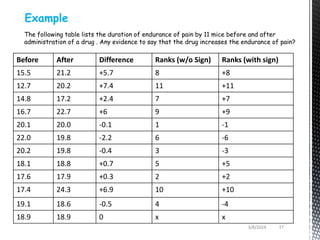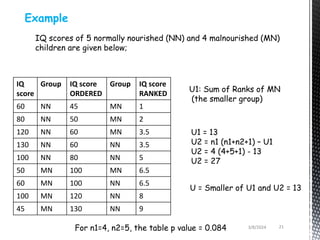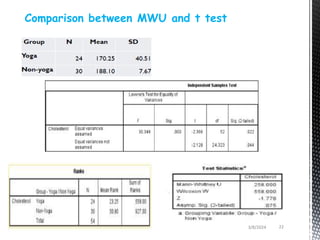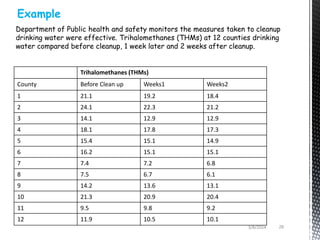- Common non-parametric tests described are the sign test, Wilcoxon signed-rank test, Mann-Whitney U test, and Kruskal-Wallis one-way ANOVA. Examples are provided to demonstrate how to perform and interpret each test. - Non-parametric tests are recommended when the data does not

1. Sumit Kumar Das
PhD Student
Dept of Biostatistics
NIMHANS
Non-Parametric Statistics

2. Levels of Measurement
Nominal – Gender, Race, Blood group Ordinal –Socio-Economic Status, pain level
Interval –Celsius or Fahrenheit scale Ratio –Kelvin Scale, Weight, pulse rate
3/8/2024 2

3. Statistical Inference
STEPS in testing of a hypothesis
 Form a null hypothesis (Ex: No difference between two groups)
 Collect data
 Compute a test statistic (Ex: t test)
 Compute p value (critical value) for the test statistic
 Decision on the hypothesis (Ex: p ≤ .05 reject null hypothesis)
Assumptions –Normality, homogeneity of variances etc.
Descriptive Statistics
 Summarizing and organizing data and provide a more general ‘picture’
about the data
Inferential statistics
 Make inferences about the population using the sample data
3/8/2024 3

4. Are all variables normally distributed?
A normally distributed data tend to have the same number of data
point so neither side of the distribution.
Form any variables of interest, one do not know for sure about its
distribution
 Income distribution in general population
 Number of car accidents per year in a region
 Duration of illness, No. of days of hospital stay etc.
3/8/2024 4

5. Parametric Methods
The properties of a distribution are defined by its midpoint
(mean) and spread of values (SD). These measures represent
the parameters of a population.
The parametric statistical methods:
1. The data must be random and independent
2. Involve population parameters . Ex: Mean
3. The data must have at least interval level of measurement
4. Require larger sample size. Ex: Z test
5. Assumptions . Ex: Equality of variances in ANOVA, Normality in t tests
3/8/2024 5

6. Non-parametric Methods
Statistical tests that don't assume a distribution or use
parameters are called nonparametric tests
1. Samples are drawn randomly and are independent
2. Do not involve population parameters
3. No stringent assumptions about distribution
4. Use counts (frequencies) and ranks
5. They are called as distribution - free/ranking tests
6. Computationally simpler methods for smaller samples
7. Can be applied on data measured on any scale (nominal, ordinal,
interval or ratio)
3/8/2024 6

7. Why Use Non-Parametric tests?
1. Scales of measurement: Ordinal/nominal scale data
Ex: GCSscore, data from social science research problems
2. Are all variables normally distributed ??
Ex: Is income distributed normally in the population ?
Incidence rates (rare diseases)
3. Smaller sample size
4. Meeting other assumptions
Ex: Variances of the samples aren’t equal always
3/8/2024 7

8. Parametric & Non-parametric methods
Characteristics Parametric Non parametric
Variables Interval and Ratio Nominal, Ordinal
Interval, Ratio
Representative Value Mean, Median,
Mode
Median, Mode
Variation Standard Deviation Range, Quartile
Deviation
Intervals for the
measure
Mean ±SE Median with Inter
Quartile Range
(IQR)
3/8/2024 8

9. 3/8/2024 9
Commonly used non-parametric tests
Aim Parametric Non Parametric
Compare a statistic to a
hypothetical value
One-sample t-test Sign test
Compare 2 independent
means
Independent sample t-test Mann-Whitney U test
(Wilcoxon Rank Sum test)
Compare 2 paired means Paired samples t-test Wilcoxon Signed rank test
Compare more than 2
means
Analysis of Variance
ANOVA
Kruskal-Wallis test
Compare related/repeated
data
Repeated Measures
ANOVA (RMANOVA
Friedman test
Relationship between
variables
Pearson’s correlation Spearman rank correlation

10. 3/8/2024 10
Sign test
 One of the simplest and oldest of the nonparametric tests.
 Can be used as a non parametric alternative to one sample t test
Ho: The median value of the sample is equal to a stated
(hypothesized) value
12, 15, 17, 23, 15, 16, 18
12, 15, 17, 40,15, 16
Mean= 16.57, Median= 16
Mean= 19, Median= 16

11. 3/8/2024 11
Procedure for sign test
 State the hypothesis value to be tested – H0
 Number of values > stated value – refer it to as S+.
 Number of values < stated value – refer it to as S-
 Tied observations are ignored, hence reducing the effective
sample size of the test
 Smaller among S+ and S- is considered as x to look into binomial
test table for p value at (n-ties) and x
For larger samples (n>25), normal approximation formula is used

12. 3/8/2024 12
Example
The following values are the ages of students of a class. Test whether
the median age is equal to 40 or not
Age Sign
42 +
22 -
24 -
25 -
32 -
34 -
38 -
Age Sign
40 X
40 X
44 +
25 -
26 -
29 -
S+=2 S-=9
n=13-2=11
P value = 0.033
(from table)
Hence, we fail to accept Ho; the median age of the group is not equal to
40

13. 3/8/2024 13
Age H0 Sign
42 40 +
22 40 -
24 40 -
25 40 -
32 40 -
34 40 -
38 40 -
40 40 X
40 40 X
44 40 +
25 40 -
26 40 -
29 40 -
Pre Post Sign
42 44 +
22 20 -
24 21 -
25 23 -
32 30 -
34 24 -
38 30 -
40 40 X
40 40 X
44 47 +
25 23 -
26 22 -
29 28 -

14. 3/8/2024 14
Sign test for paired samples
One sample sign test is a special case of a paired sample sign test
used for paired/matched samples
Ho: The median difference between pairs is zero
Under Ho we would expect that,
No of Xpre> Xpost= No ofXpre< Xpost
i.e. half of the differences will be
positive and half will be positive
Only signs are considered for
calculations but not the magnitude of
difference. Hence, it’s a less powerful
test.
Pre Post Difference
42 45 +
22 20 -
24 21 -
25 20 -
32 31 -
34 48 +
38 25 -
25 26 +
18 28 +
26 26 X

15. 3/8/2024 15
Wilcoxon Signed rank test
 To compare two related/ matched samples or repeated
measurements on a single sample to assess whether their population
mean ranks differ.
 It corresponds to paired t-test in parametric methods
 It takes into account direction & magnitude of the difference
 This is also called as Wilcoxon paired-sample test
Ho: The median difference is zero
or
Ho: There is no difference in median of paired values

16. 3/8/2024 16
Procedure for WSR test
 Compute the difference between each paired values (ignore the
ties)
 Rank the differences (ascending / descending order) without
considering the sign of the difference
 Attach the corresponding signs after assigning the ranks
 T + = Sum of the positive ranks
 T - = Sum of the negative ranks
 T = Smaller of T + and T –
 Get the table value corresponding to sample size (n - ties)
For larger samples use normal approximation formula

17. 3/8/2024 17
Example
The following table lists the duration of endurance of pain by 11 mice before and after
administration of a drug . Any evidence to say that the drug increases the endurance of pain?
Before After Difference Ranks (w/o Sign) Ranks (with sign)
15.5 21.2 +5.7 8 +8
12.7 20.2 +7.4 11 +11
14.8 17.2 +2.4 7 +7
16.7 22.7 +6 9 +9
20.1 20.0 -0.1 1 -1
22.0 19.8 -2.2 6 -6
20.2 19.8 -0.4 3 -3
18.1 18.8 +0.7 5 +5
17.6 17.9 +0.3 2 +2
17.4 24.3 +6.9 10 +10
19.1 18.6 -0.5 4 -4
18.9 18.9 0 x x

18. 3/8/2024 18
Example (contd.)
T+ = Sum of Positive Ranks = 14
T-= Sum of Negative Ranks = 52
T = Smaller of T+ and T-
T = 14
For n=11, table P value= 0.091
Conclusion: The difference in the sum of positive and negative ranks is
statistically not significant
or
The median duration of pain endurance is not different after giving
the drug

19. 3/8/2024 19
Mann-Whitney U test
Non – parametric analogue of independent samples t test. Used in
situations where,
 The data doesn’t follow normal distribution
 Two samples are grossly different in size & variance
 Data is in ordinal scale or ranks
Ho: Two groups have similar distributions or
Ho: Two independent samples come from the same population or
Ho: Median of two independent samples are equal
This test is also known as Mann-Whitney-Wilcoxon (MWW) Test or
Wilcoxon Rank-Sum Test

20. 3/8/2024 20
Procedure for MW U test
 Rank (ascending / descending order ) all the values in the
two groups taken together
 Tied values should be given average ranks
 U1 = Sum of the ranks of smaller group
 U2=n1 (n1+n2+1) – U1
 U = Smaller of U1 and U2
 Get the table value (sampling distribution of U)
corresponding to n1 & n2 & U
For larger samples use normal approximation formula

21. 3/8/2024 21
Example
IQ scores of 5 normally nourished (NN) and 4 malnourished (MN)
children are given below;
IQ
score
Group IQ score
ORDERED
Group IQ score
RANKED
60 NN 45 MN 1
80 NN 50 MN 2
120 NN 60 MN 3.5
130 NN 60 NN 3.5
100 NN 80 NN 5
50 MN 100 MN 6.5
60 MN 100 NN 6.5
100 MN 120 NN 8
45 MN 130 NN 9
U1: Sum of Ranks of MN
(the smaller group)
U1 = 13
U2 = n1 (n1+n2+1) – U1
U2 = 4 (4+5+1) - 13
U2 = 27
For n1=4, n2=5, the table p value = 0.084
U = Smaller of U1 and U2 = 13

22. 3/8/2024 22
Comparison between MWU and t test

23. 3/8/2024 23
Kruskal-Wallis one way ANOVA
This test is used as nonparametric alternative to one way ANOVA.
It tests whether several (three or more) samples come from the
same population or not.
Ho: Samples have similar distributions or
Ho: The median values in different groups are the same
 Uses Chi Square distribution with k–1 df
 K=Number of groups/ Factors/ Levels

24. 3/8/2024 24
Procedure of KW test
 Rank the values taking all values (irrespective of the groups) together
 Calculate the test statistic
𝐻 = (
12
𝑛(𝑛+1)
𝑅𝑗2
𝑛𝑗
) − 3 (n+1)
n= Total of sample size
𝑅𝑗 = The sum of the ranks of ith group (i=1,..,k)
k is the number of groups
 H is distributed as chi square distribution with (k-1) df
 Reject H0 if H is more than chi square table value
 If the global H0 is rejected, pairwise group differences should be
tried using MW U test for each pairs with correction

25. 3/8/2024 25
Example
Diastolic Blood Pressure (DBP - mm/Hg) measured for patients with 3 Socio
Economic backgrounds. Is there any reason to believe that the 3 groups differ with
respect to this characteristic?
Group I Ranks I
100 13
103 15
89 7
78 1
105 16
Group 2 Ranks 2
92 9
97 11
88 6
84 4
90 8
95 10
Group 3 Ranks 3
81 2
102 14
86 5
83 3
99 12
 Ranking is done irrespective of the group
 Number in each group need not be equal

26. 3/8/2024 26
Example (contd.)
𝐻 = (
12
𝑛(𝑛+1)
𝑅𝑗2
𝑛𝑗
) − 3 (n+1)
H = 52.2 – 51 =1.2
Hence, the difference in median DBP values of 3 SES groups are
statistically not significant
Table value (chi square table) with 2 df table P value=0.539

27. 3/8/2024 27
Friedman’s test
 It is non-parametric alternative of repeated measures ANOVA
 Groups that is measured for three or more times
𝐻 =
12
𝑛𝑘 𝑛+1
𝑅𝑗2
− 3n(k+1)
k is the number of times the measurement is taken
n is the number of subjects
Rj is the sum of the ranks in the column

28. 3/8/2024 28
Example
Trihalomethanes (THMs)
County Before Clean up Weeks1 Weeks2
1 21.1 19.2 18.4
2 24.1 22.3 21.2
3 14.1 12.9 12.9
4 18.1 17.8 17.3
5 15.4 15.1 14.9
6 16.2 15.1 15.1
7 7.4 7.2 6.8
8 7.5 6.7 6.1
9 14.2 13.6 13.1
10 21.3 20.9 20.4
11 9.5 9.8 9.2
12 11.9 10.5 10.1
Department of Public health and safety monitors the measures taken to cleanup
drinking water were effective. Trihalomethanes (THMs) at 12 counties drinking
water compared before cleanup, 1 week later and 2 weeks after cleanup.

29. 3/8/2024 29
County Within-subjects ranks
Rank 1 Rank 2 Rank 3
1 21.1(3) 19.2(2) 18.4(1)
2 24.1(3) 22.3(2) 21.2(1)
3 14.1(3) 12.9(1.5) 12.9(1.5)
4 18.1(3) 17.8(2) 17.3(1)
5 15.4(3) 15.1(2) 14.9(1)
6 16.2(3) 15.1(1.5) 15.1(1.5)
7 7.4(3) 7.2(2) 6.8(1)
8 7.5(3) 6.7(2) 6.1(1)
9 14.2(3) 13.6(2) 13.1(1)
10 21.3(3) 20.9(2) 20.4(1)
11 9.5(2) 9.8(3) 9.2(1)
12 11.9(3) 10.5(2) 10.1(1)
𝑅𝑗2
35 24 13
Example (Cont…)
𝐻 =
12
𝑛𝑘 𝑛+1
𝑅𝑗2
− 3n(k+1)
𝐻 =
12
12𝑥3𝑥 3+1
(352
+ 242
+ 132
) −
3x12x(3+1)
For the values of independent subjects (n)
greater than 20 and/or values of groups (k)
greater than 6, use χ2 table with k-1 degrees
of freedom otherwise use the Friedman table
Calculated H value is greater than the critical
value of H for a 0.05 significance level.
Hcalculated >Hcritical hence reject the null
hypotheses.
For n=12, k=3, α=5% the Hcritical is 6.5
H= 20.16

30. 3/8/2024 30
Non-parametric methods
Aim Tests
Association and agreement Chi square/ Fisher’s exact test; Contingency
coefficients; Kendall’s Tau; Kappa coefficient
Comparison of two
independent samples
Fisher’s exact test; Median test; WMW U test; KS
test; Moses test
Comparison of multiple
independent samples
Kruskal-Wallis test; Extended median test
Comparison of two
dependent samples
McNemar’s test; Sign test for two samples; WSR
test
Comparison of multiple
independent samples
Cochran’s Q test; Friedman’s ANOVA; Kendal’s
CoC
Analysis of single samples Binomial test; Sign test for one sample ; Test for
randomness; Chi square for GOF test; KS one
sample test

31. 3/8/2024 31
Merits and Demerits
Merits:
1. Used with all scales
2. Easier to compute for small samples
3. Make Fewer Assumptions
4. Need not involve population parameters
5. Applied on any type of data
6. Avoids problems of transformation (Ex: interpretation)
7. Can be much more efficient than parametric methods when
distributions are notnormal
Demerits:
1. Less powerful in detecting differences
2. May waste/discard information
3. Difficult to compute by hand for large
samples
4. Covariate analyses can’t be done.

32. 3/8/2024 32
Why not use NP tests all the time?
Since non parametric tests require fewer assumptions and can be
used with a broader range of data types, this question arises!!
Parametric and non-parametric methods often address two different
types of questions.
Parametric tests are often preferred because:
 They are more robust
 They don’t discard any information in the data
 Under ideal conditions, parametric tests are more powerful

33. 3/8/2024 33
THANK YOU