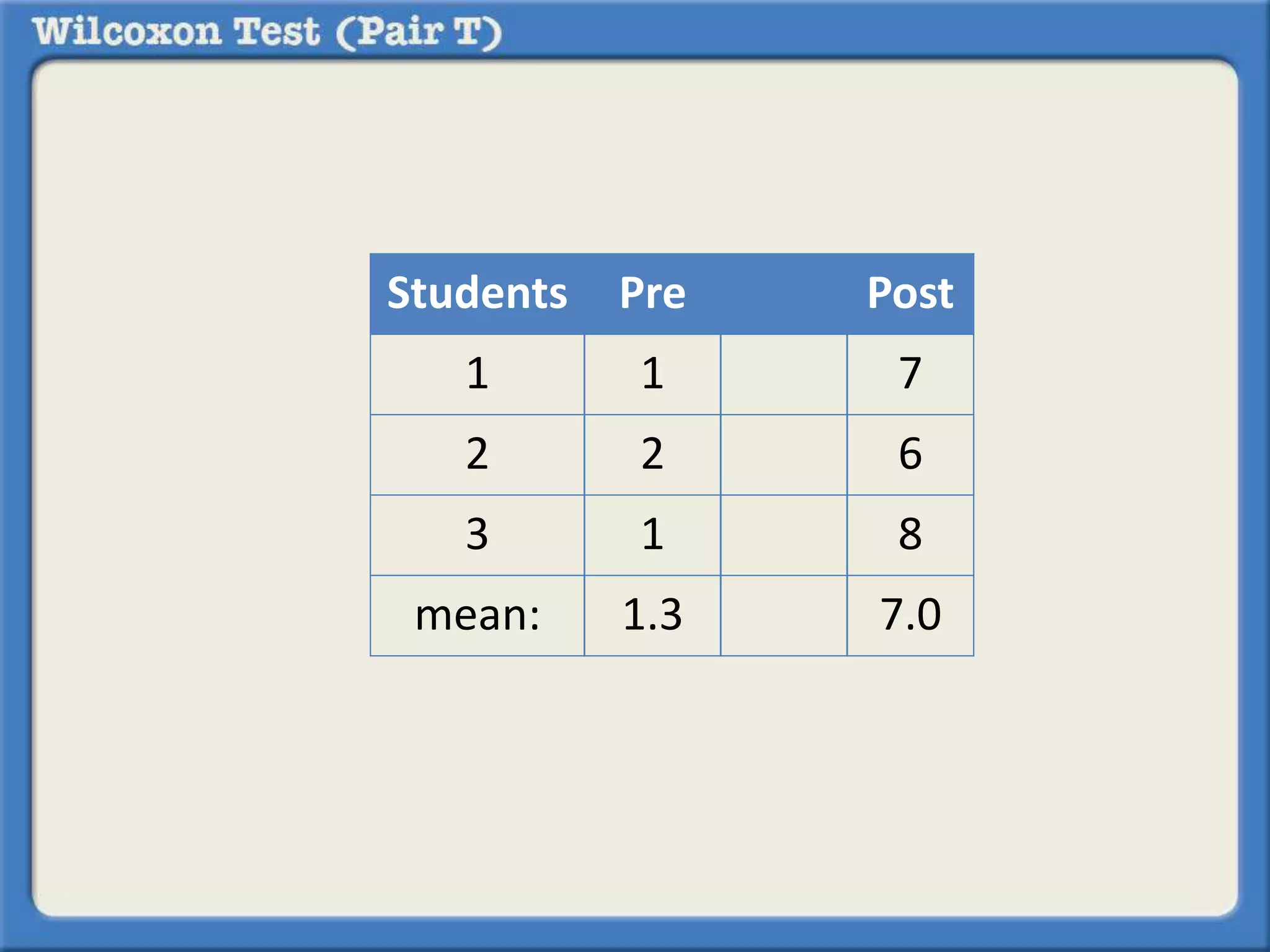
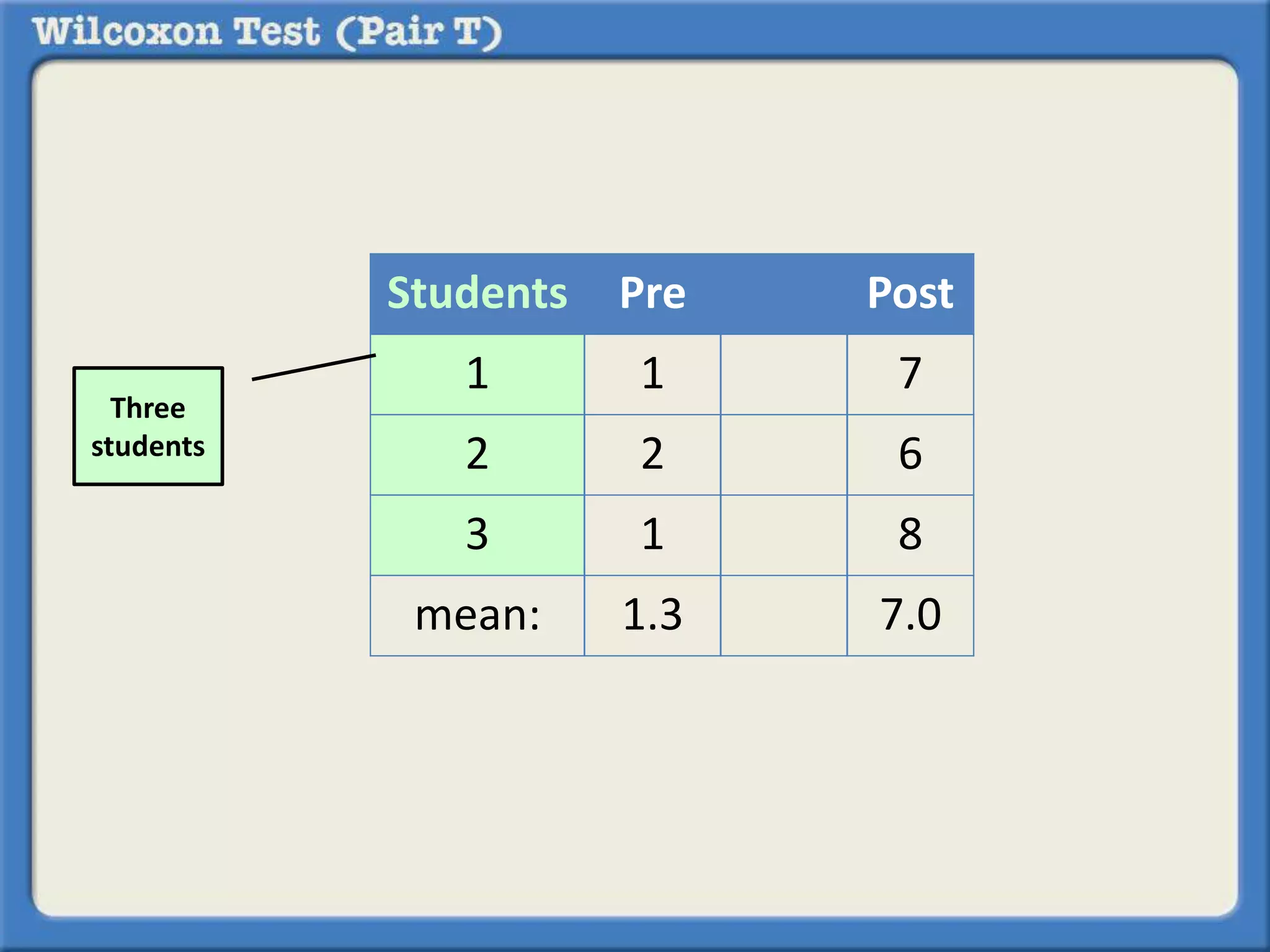
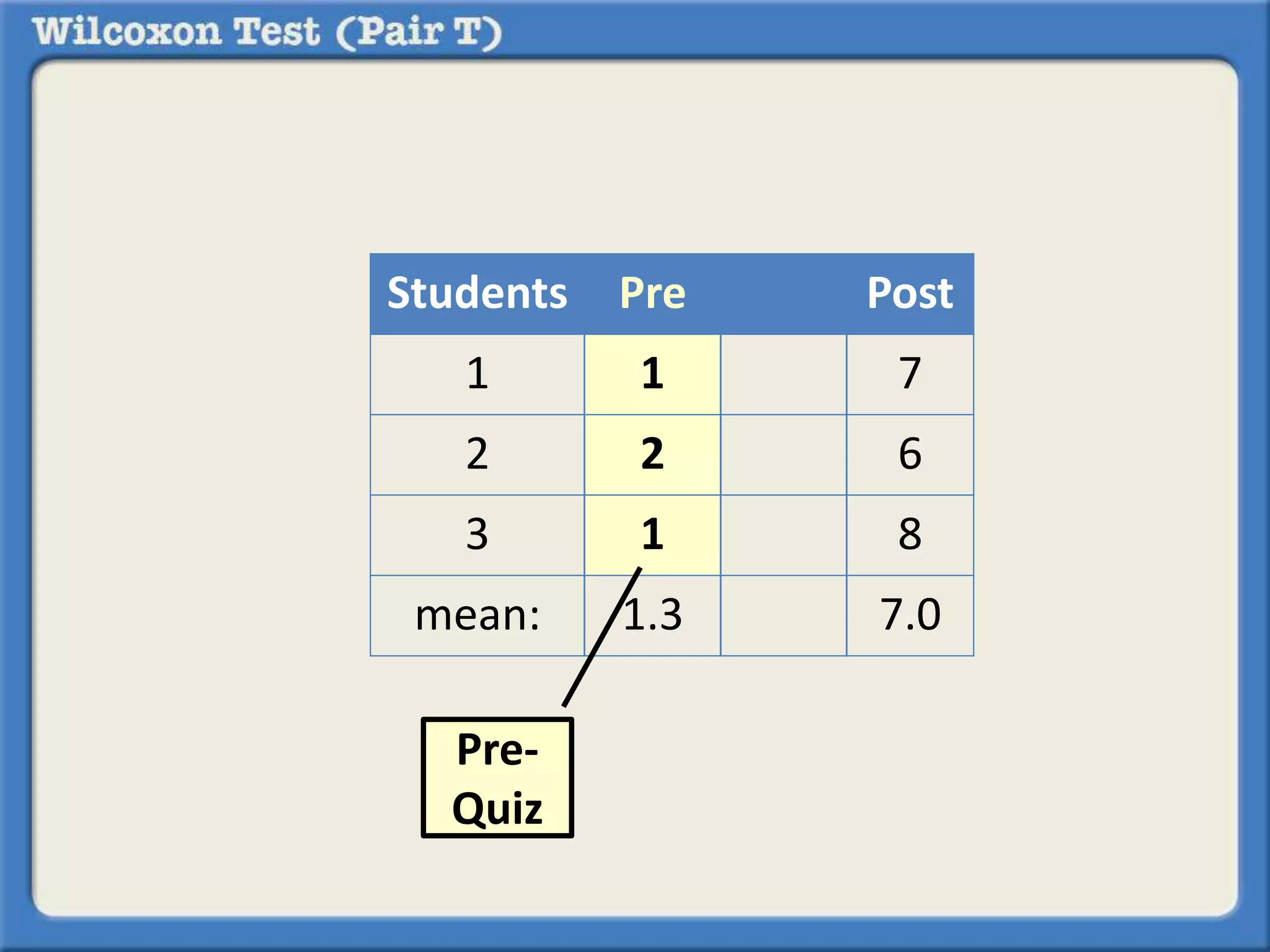
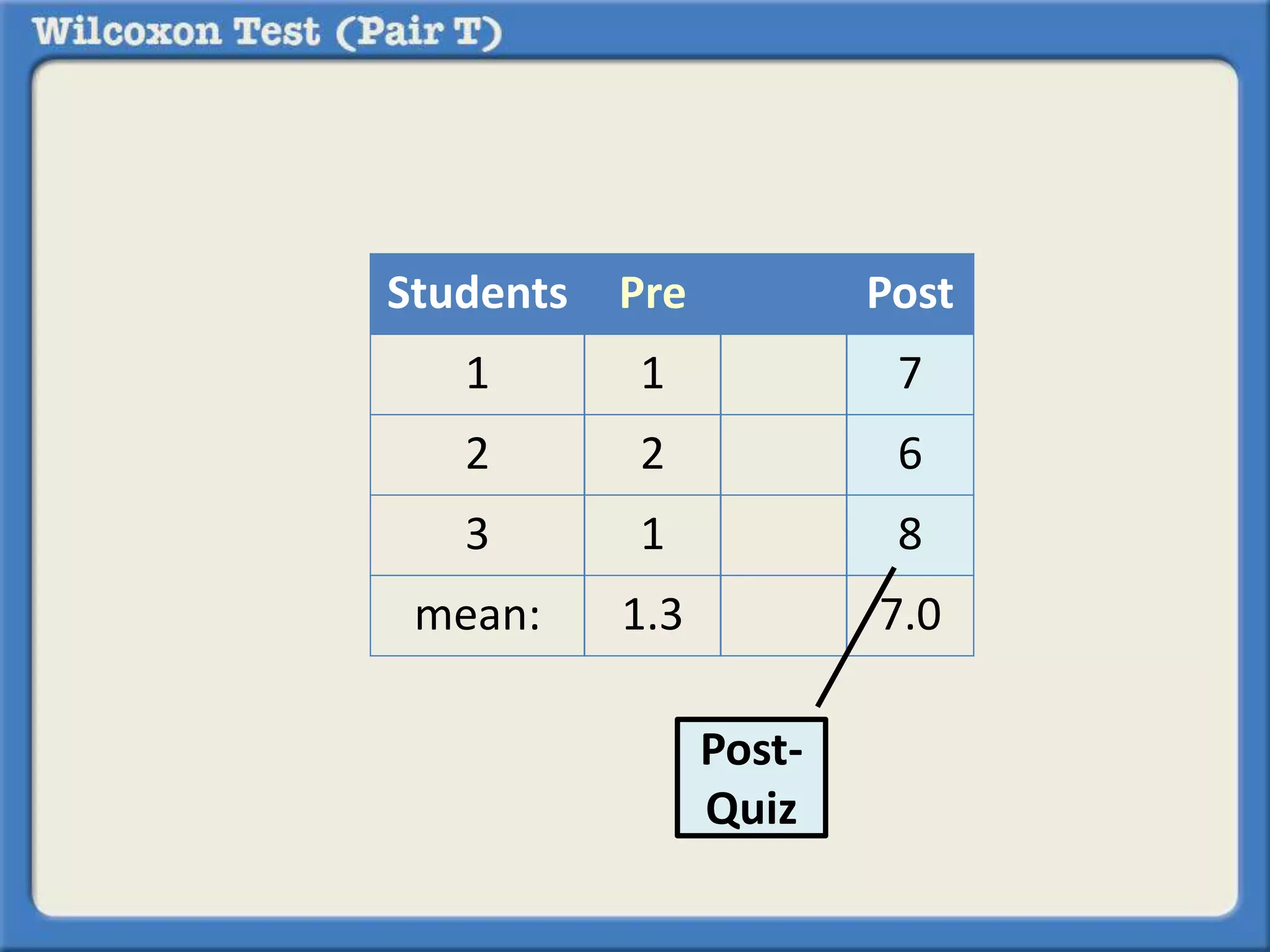
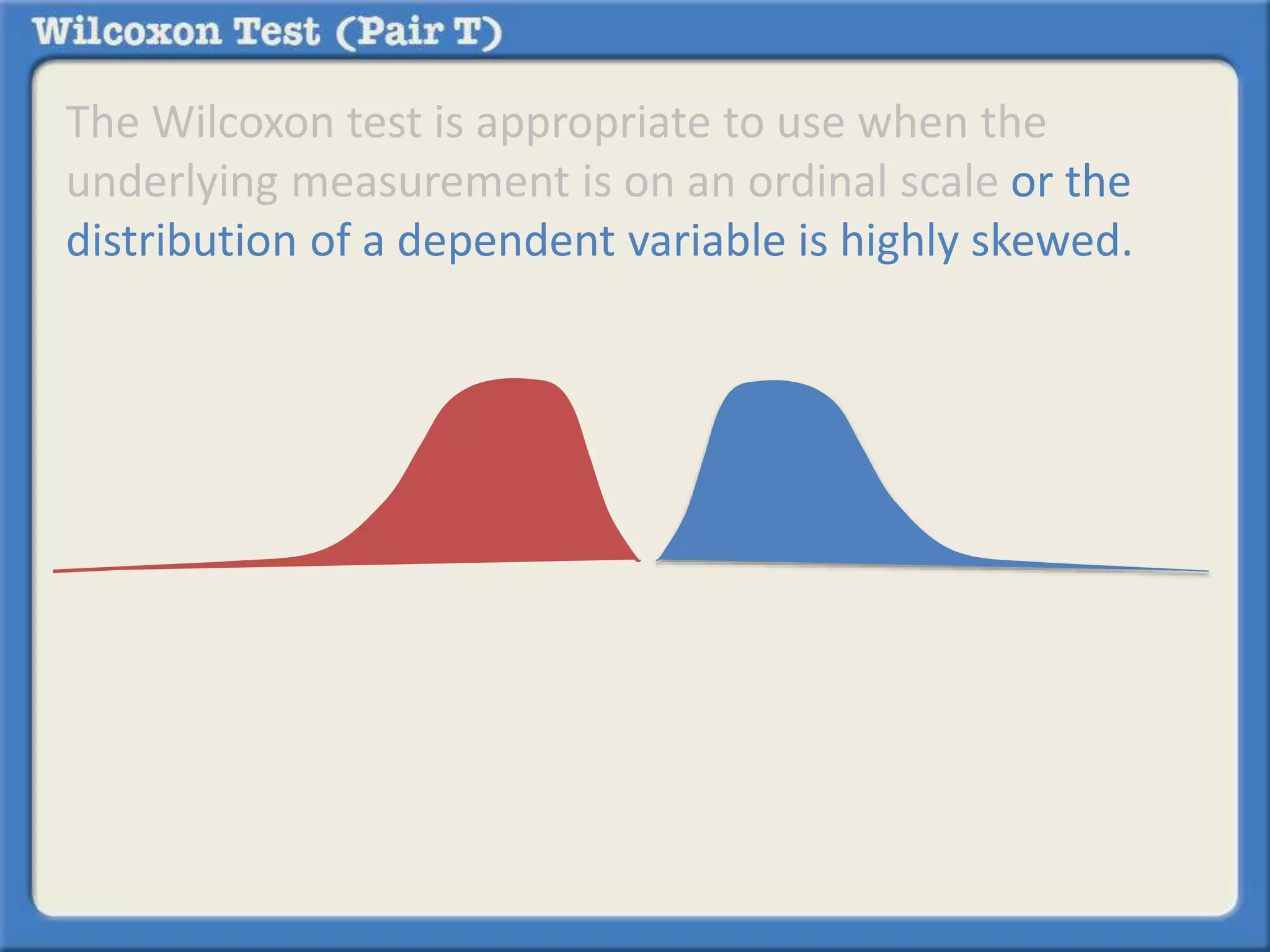
The Wilcoxon Signed-Ranked Test is a non-parametric statistical hypothesis test used to compare two related samples, such as the same set of observations measured under two different conditions, to assess whether their population mean ranks differ. It can be used as an alternative to the paired Student's t-test when the assumption of normality is not met or the data is only on an ordinal scale. Like the paired t-test, it tests whether the mean or median of the differences between paired observations is significantly different from zero.

1. Wilcoxon Signed-Ranked Test
(Paired T)

2. The Wilcoxon test is the non-parametric analogue to the
pair-wise (repeated measures) t-test.

3. The non-parametric analogue to the pair-wise (repeated
measures) t-test is the Wilcoxon test.
You may remember that the pair-wise (repeated
measures) t-test is used to determine the statistical
significant difference between the same
sample/observations or people on two separate
occasions.

4. Here is a simplified data set that would use a paired
sample t-test:

5. Students Pre Post
1 1 7
2 2 6
3 1 8
mean: 1.3 7.0

6. Students Pre Post
1 1 7
2 2 6
3 1 8
mean: 1.3 7.0
Three
students

7. Students Pre Post
1 1 7
2 2 6
3 1 8
mean: 1.3 7.0
Pre-
Quiz

8. Students Pre Post
1 1 7
2 2 6
3 1 8
mean: 1.3 7.0
Students Receive
Instruction

9. Students Pre Post
1 1 7
2 2 6
3 1 8
mean: 1.3 7.0
Post-
Quiz

10. Students Pre Post
1 1 7
2 2 6
3 1 8
mean: 1.3 7.0
The Mean
of the
Pre-quiz

11. Students Pre Post
1 1 7
2 2 6
3 1 8
mean: 1.3 7.0
The Mean
of the
Pre-quiz
is compared to

12. Students Pre Post
1 1 7
2 2 6
3 1 8
mean: 1.3 7.0
The Mean
of the
Pre-quiz
is compared to
The Mean
of the
Post-quiz

13. Students Pre Post
1 1 7
2 2 6
3 1 8
mean: 1.3 7.0
The Mean
of the
Pre-quiz
is compared to
The Mean
of the
Post-quiz
using a Paired-
Sample t-test

14. It appears that the post-test scores are higher than the
pre-test scores. But what is the likelihood of getting this
result if we tested one thousand samples of 3.0?

15. It appears that the post-test scores are higher than the
pre-test scores. But what is the likelihood of getting this
result if we tested one thousand samples of 3.0?
We use the paired-sample t-test to test the likelihood of
this result occurring by chance.

16. It appears that the post-test scores are higher than the
pre-test scores. But what is the likelihood of getting this
result if we tested one thousand samples of 3.0?
We use the paired-sample t-test to test the likelihood of
this result occurring by chance.
But the Paired-sample t-test can be used when certain
assumptions are met:

17. It appears that the post-test scores are higher than the
pre-test scores. But what is the likelihood of getting this
result if we tested one thousand samples of 3.0?
We use the paired-sample t-test to test the likelihood of
this result occurring by chance.
But the Paired-sample t-test can be used when certain
assumptions are met:
1. the data is interval/ratio

18. It appears that the post-test scores are higher than the
pre-test scores. But what is the likelihood of getting this
result if we tested one thousand samples of 3.0?
We use the paired-sample t-test to test the likelihood of
this result occurring by chance.
But the Paired-sample t-test can be used when certain
assumptions are met:
1. the data is interval/ratio
2. the data is normally distributed

19. The Wilcoxon test is appropriate to use when the
underlying measurement is on an ordinal scale.

20. The Wilcoxon test is appropriate to use when the
underlying measurement is on an ordinal scale.
3rd
Place
15’2”
2nd
Place
16’1”
1st
Place
16’3”

21. The distance between 3rd and 2nd place (11”) is not the
same interval as the distance between 2nd and 1st
3rd
Place
15’2”
2nd
Place
16’1”
1st
Place
16’3”
place (1”)

22. The Wilcoxon test is appropriate to use when the
underlying measurement is on an ordinal scale or the
distribution of a dependent variable is highly skewed.

23. The Wilcoxon test is appropriate to use when the
underlying measurement is on an ordinal scale or the
distribution of a dependent variable is highly skewed.

24. The Wilcoxon test is appropriate to use when the
underlying measurement is on an ordinal scale or the
distribution of a dependent variable is highly skewed.
Like the Paired Sample t-test, the Wilcoxon test will
compare whether there are significant differences
between the distributions between time-one and time-two.

25. Time 1 for Distribution A Time 2 for Distribution A
0 0

26. A Paired Sample t-test would be used if the distributions
were more normal and the data were interval or ratio.

27. A Paired Sample t-test would be used if the distributions
were more normal and the data were interval or ratio.
Interval/Ratio scales
• assume quantity of the attribute.
• have equal intervals.

28. The Wilcoxon like all nonparametric tests

29. The Wilcoxon like all nonparametric tests
1. is not sensitive to outliers and therefore is more
appropriate to use when the data is skewed.

30. The Wilcoxon like all nonparametric tests
1. is not sensitive to outliers and therefore is more
appropriate to use when the data is skewed.
2. (uses the Median instead of the Mean and is
therefore more appropriate to use when the data is
rank order or ordinal.