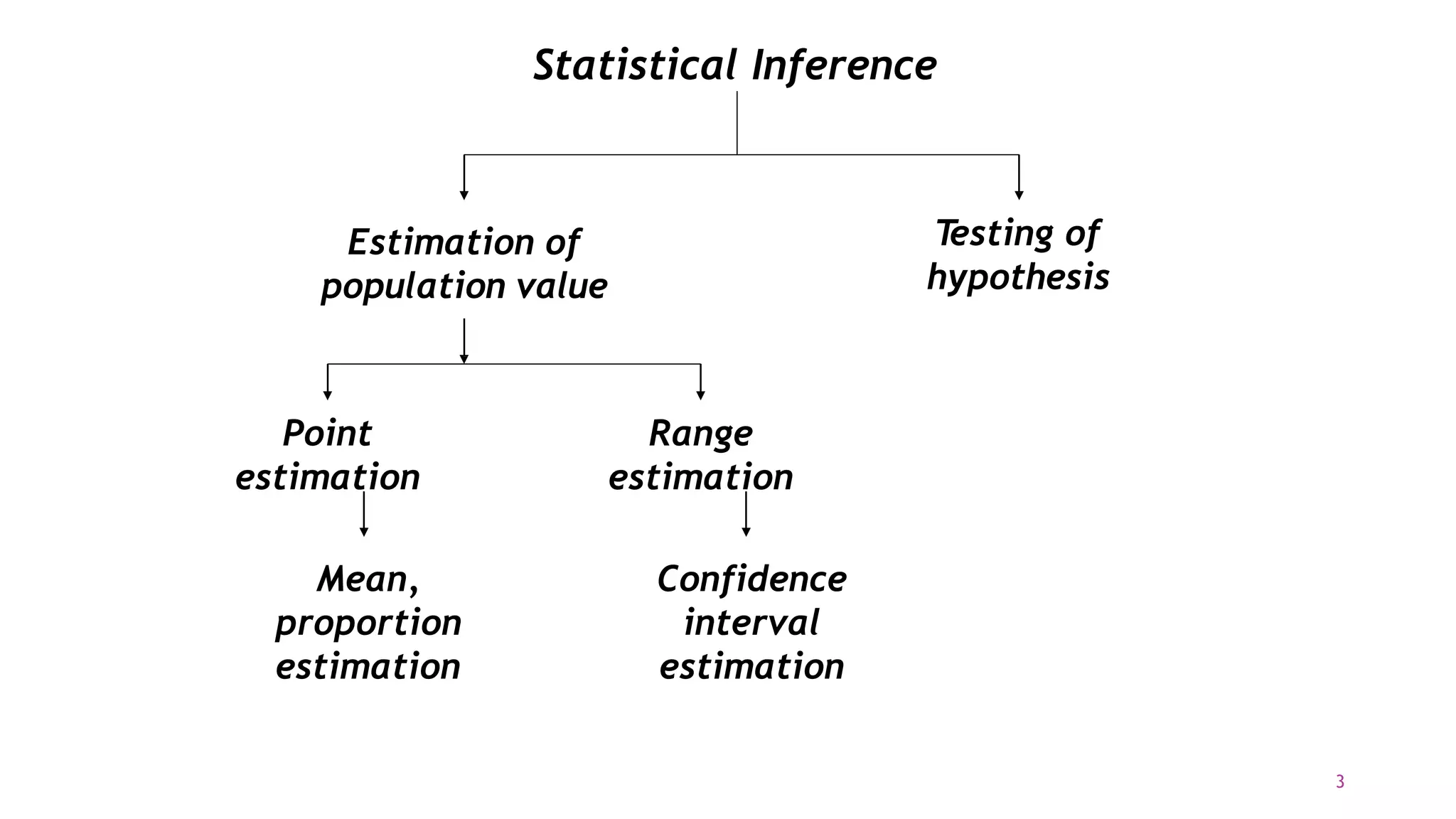
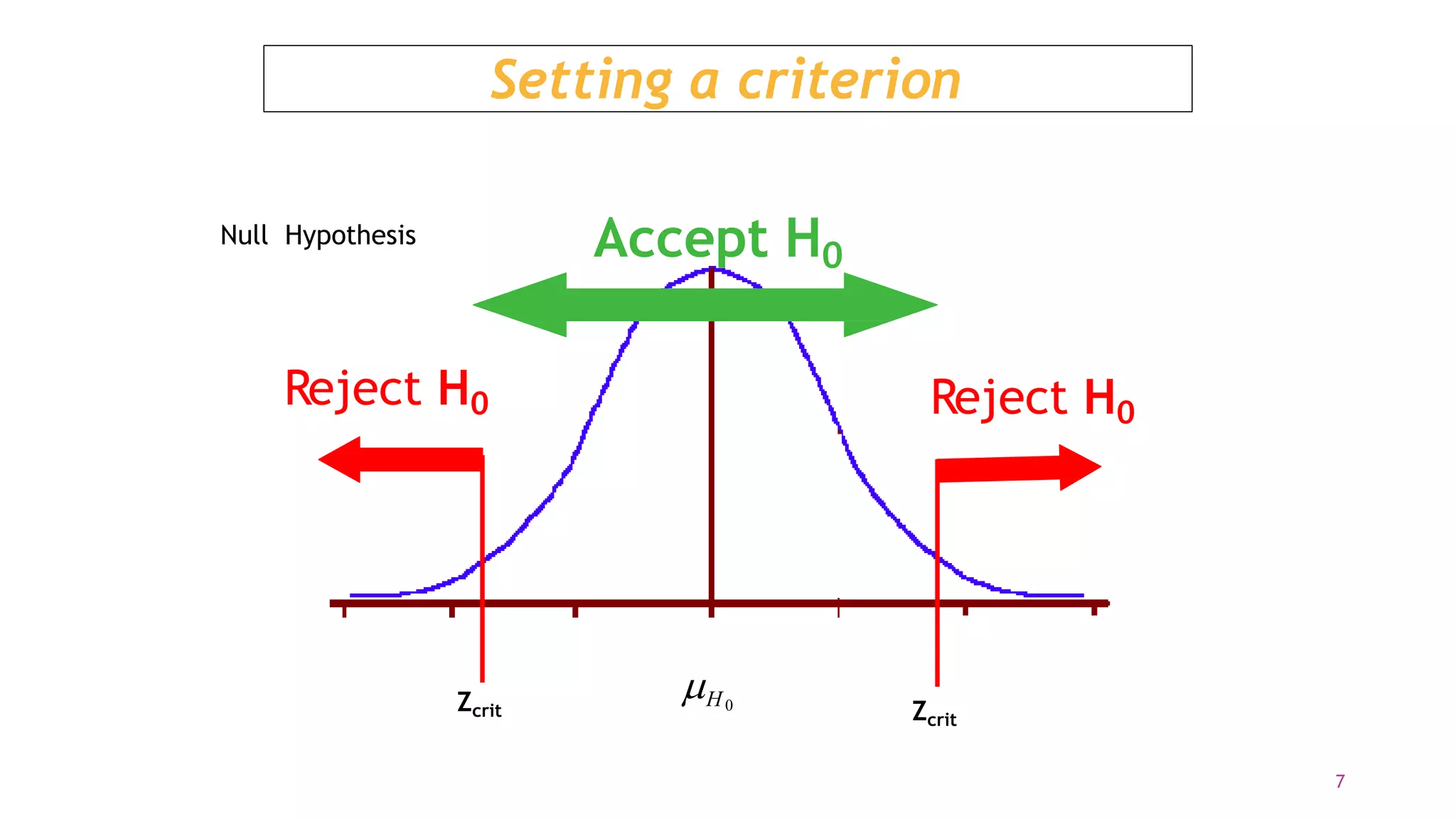
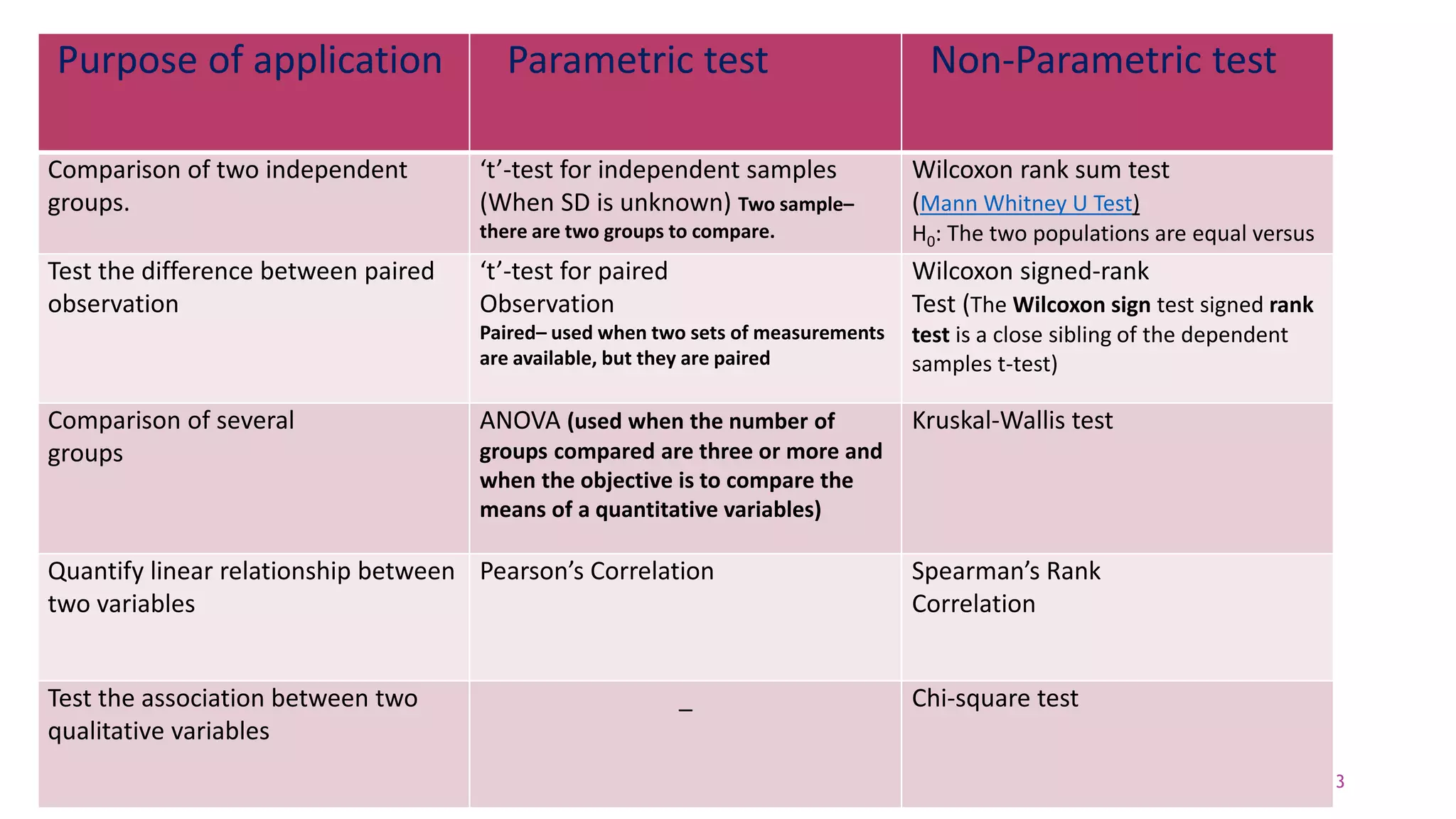
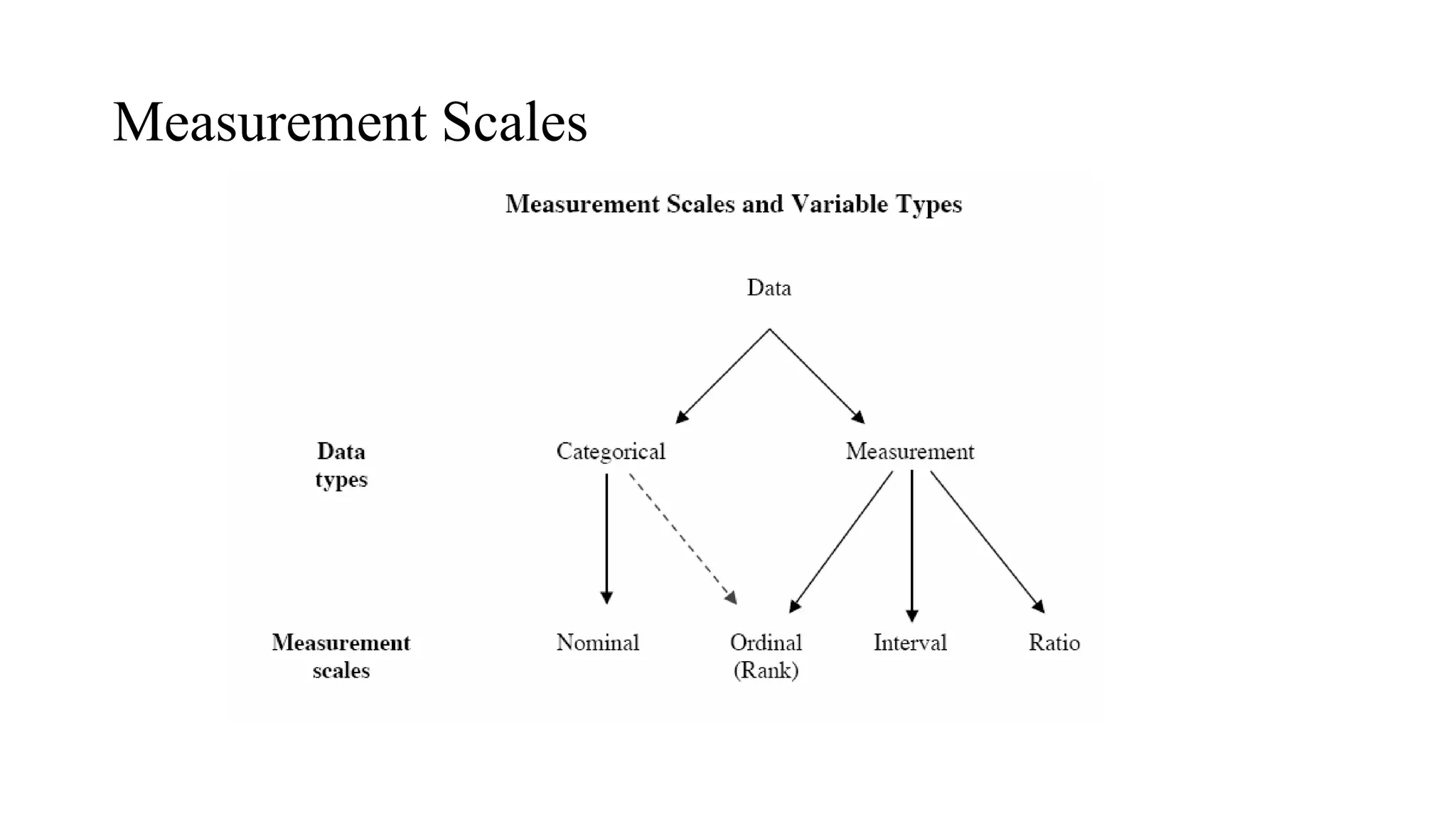
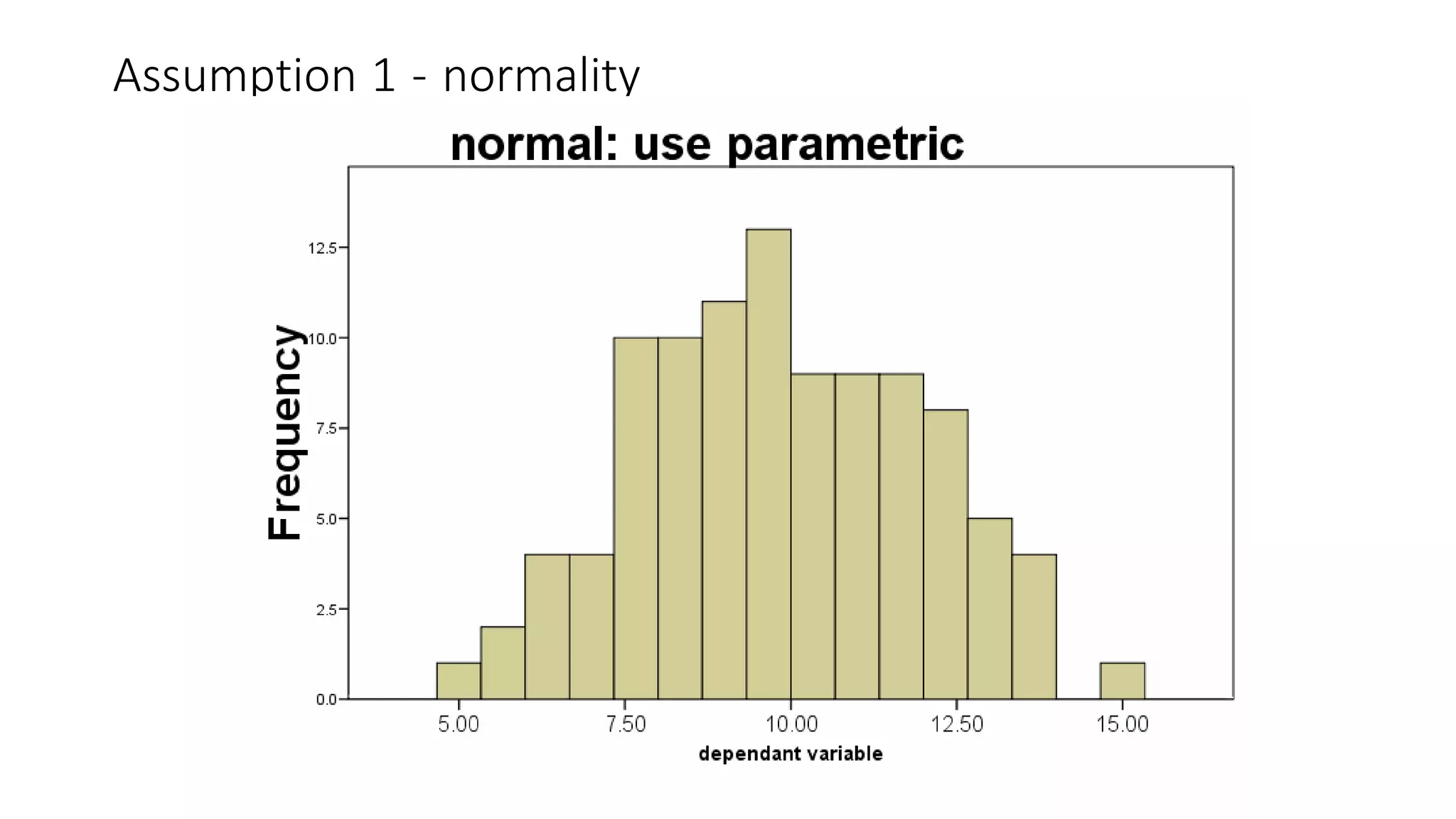
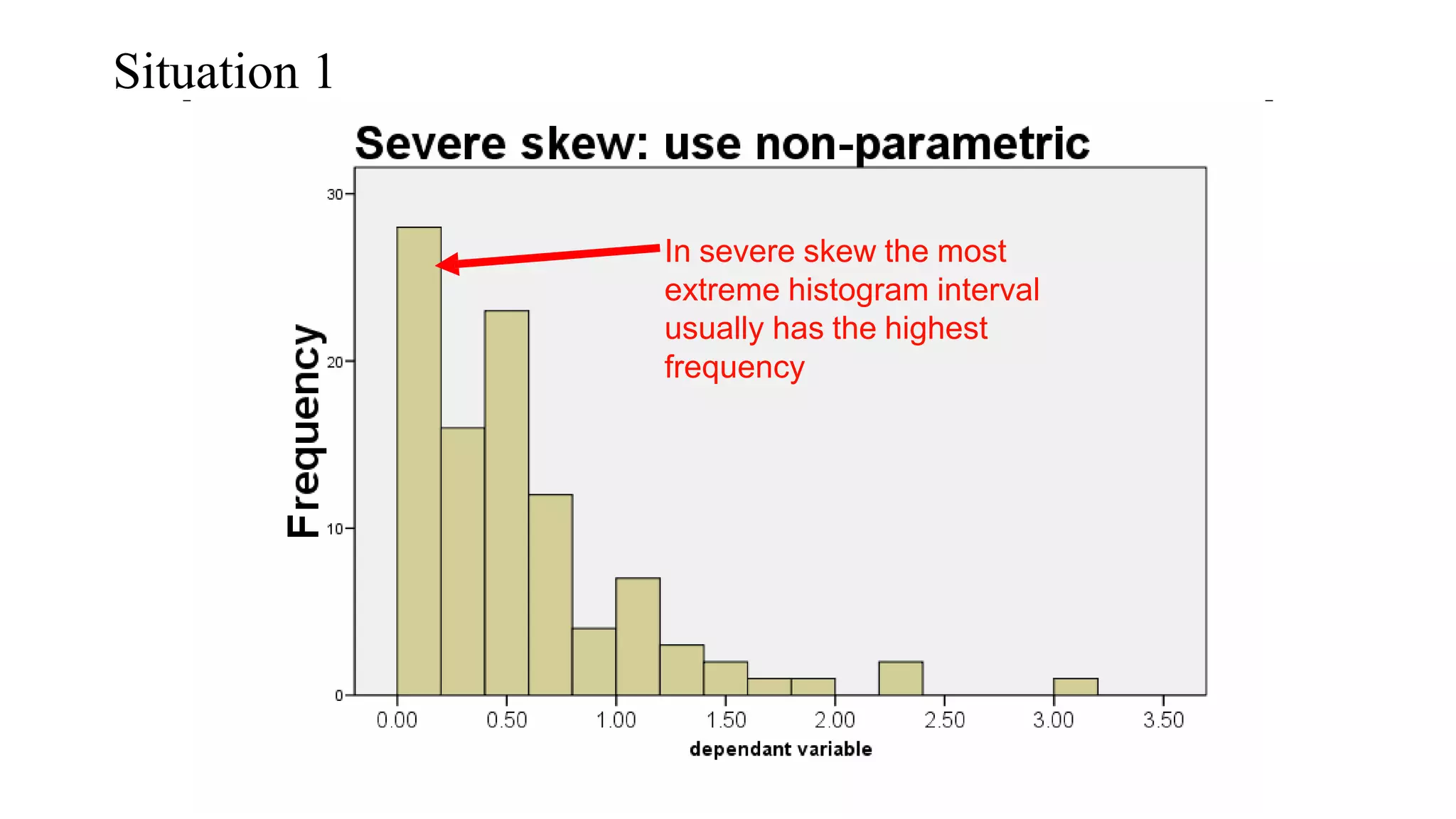
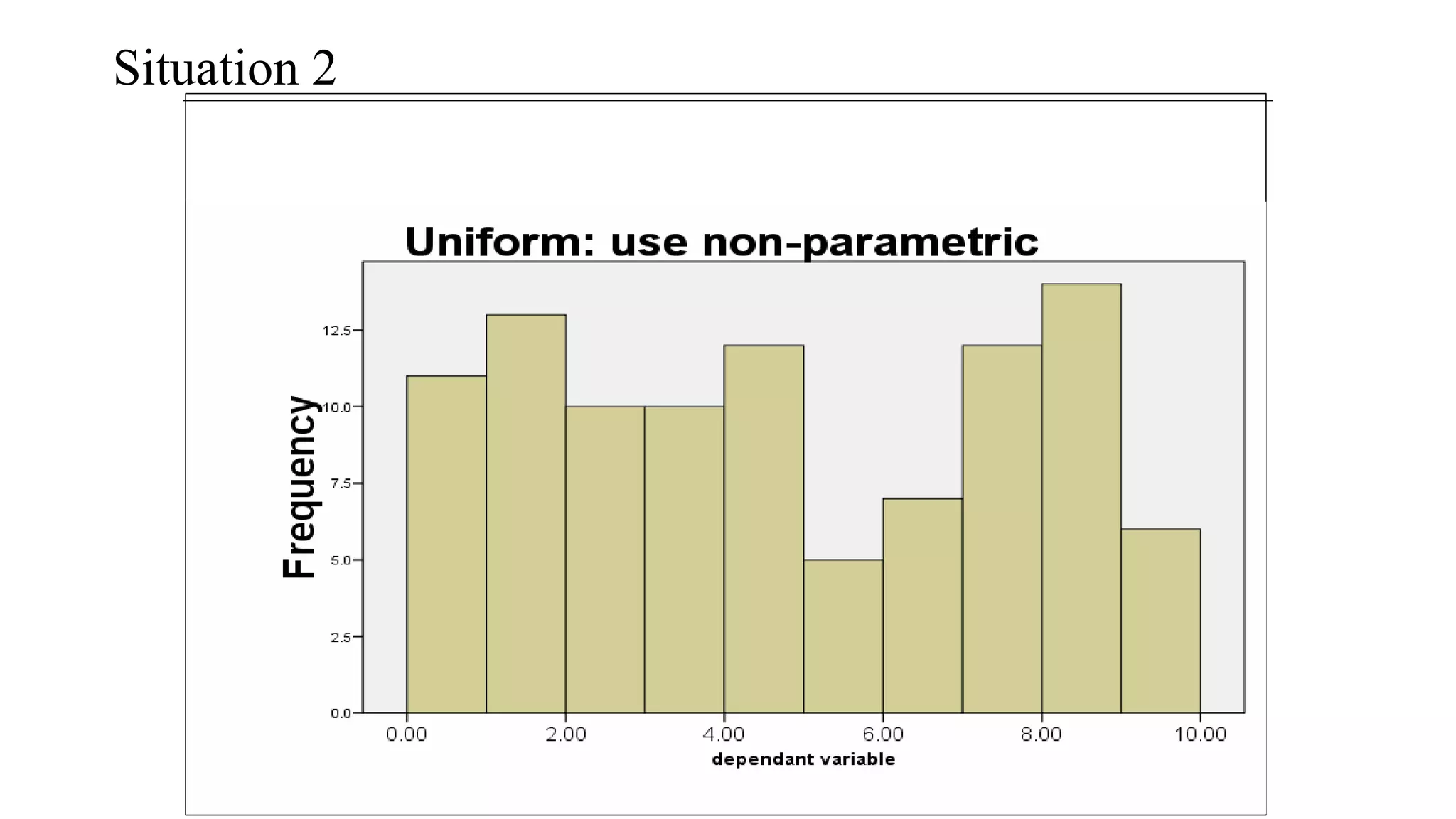
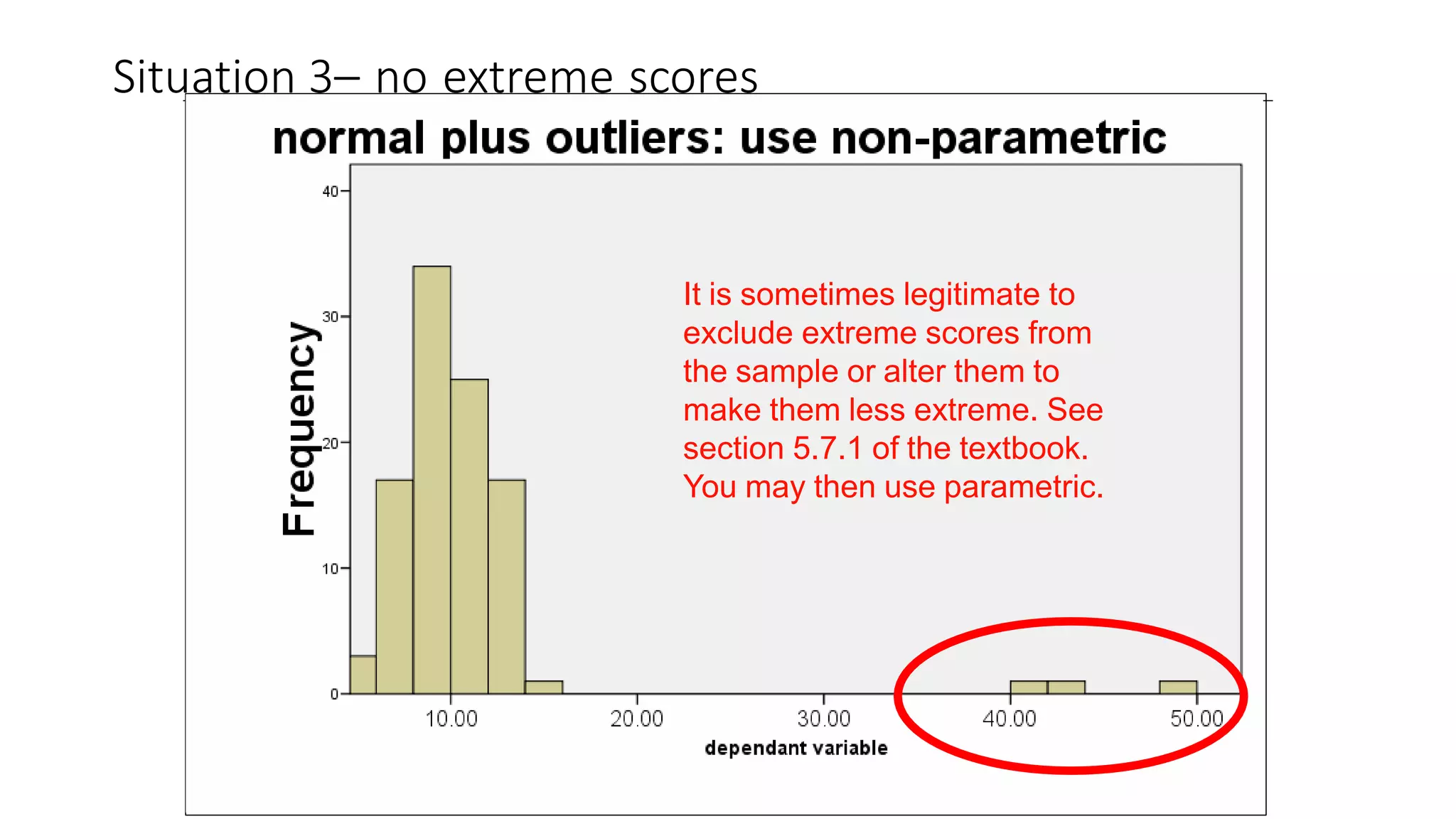
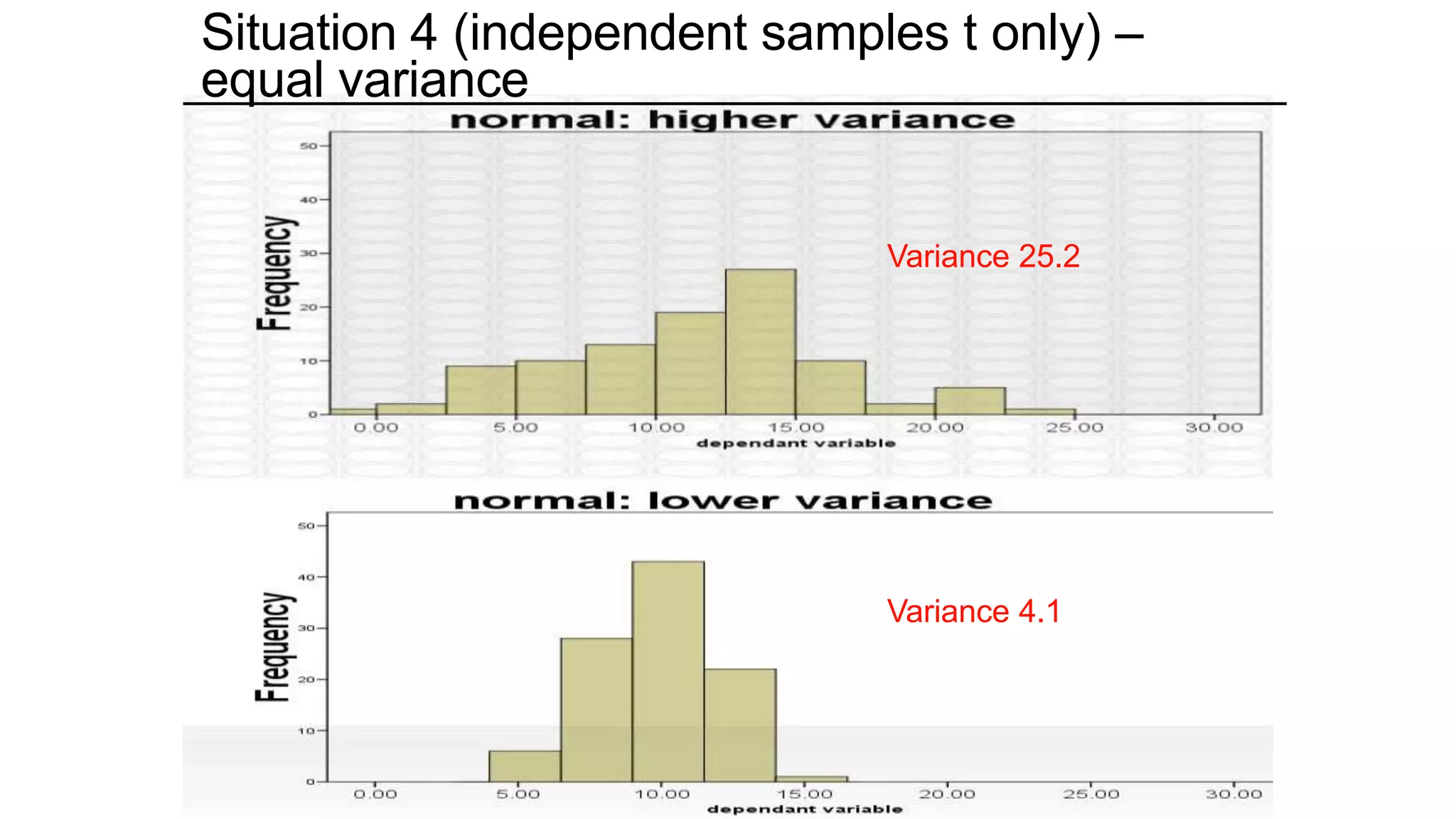
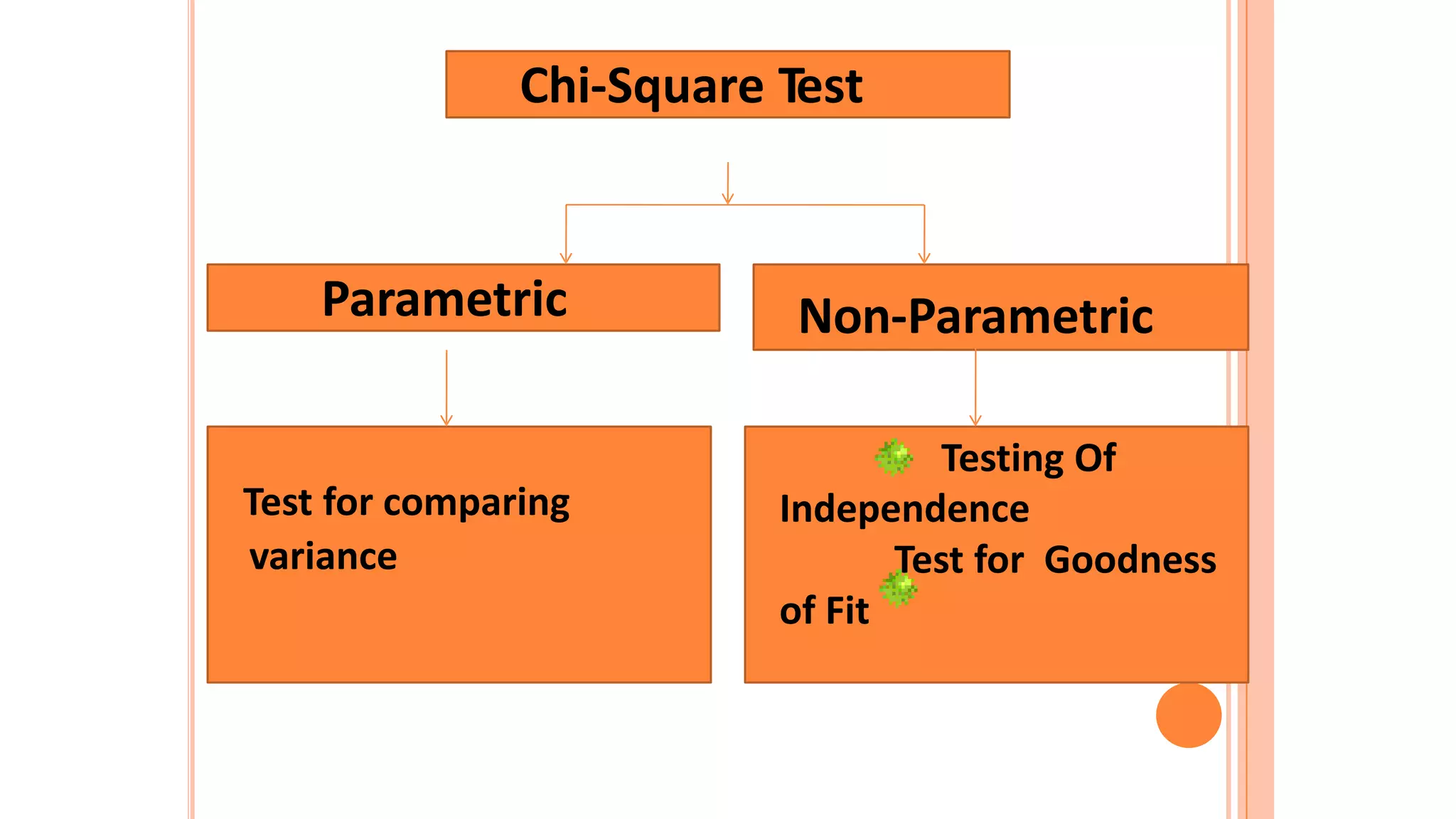
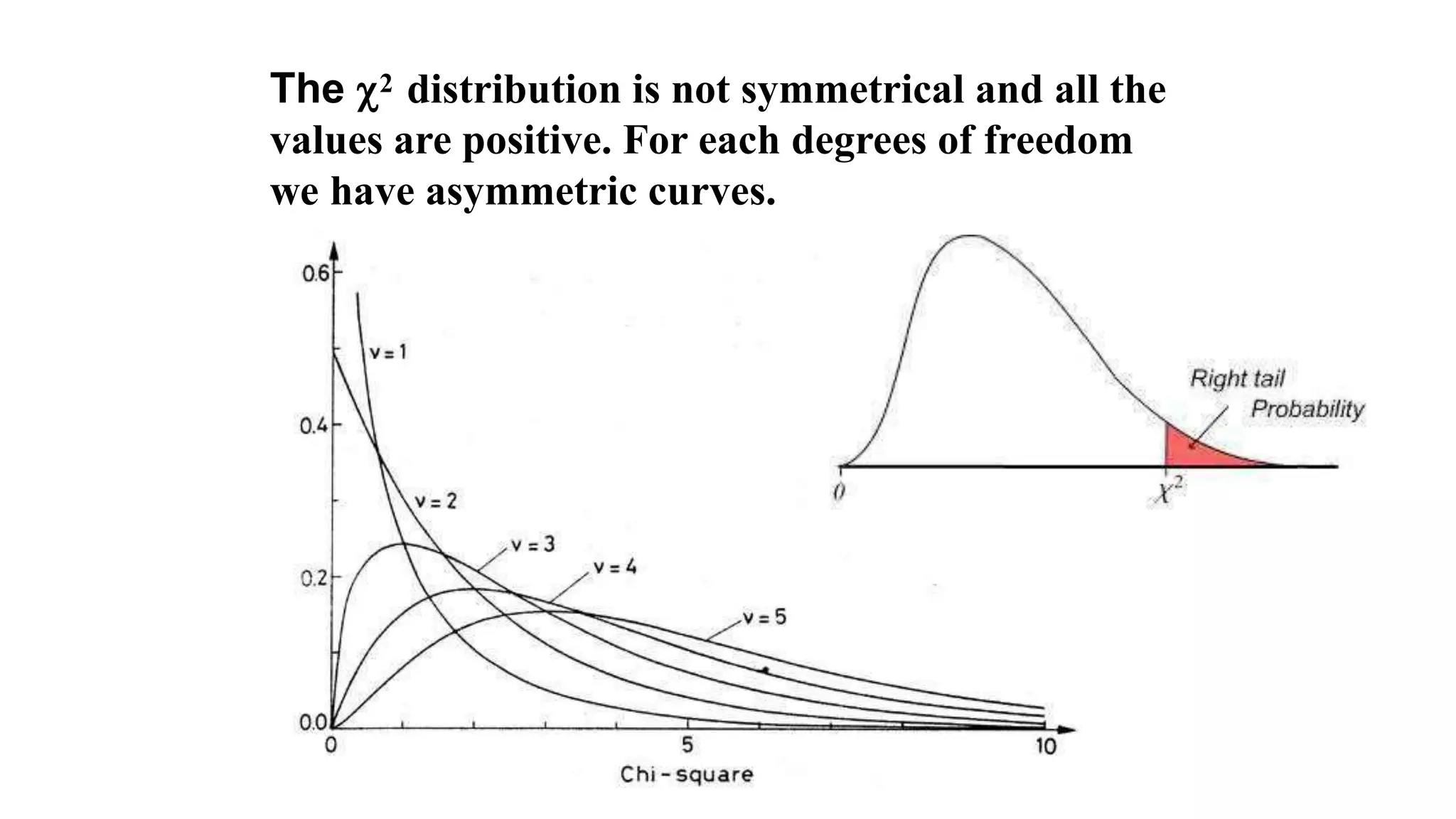
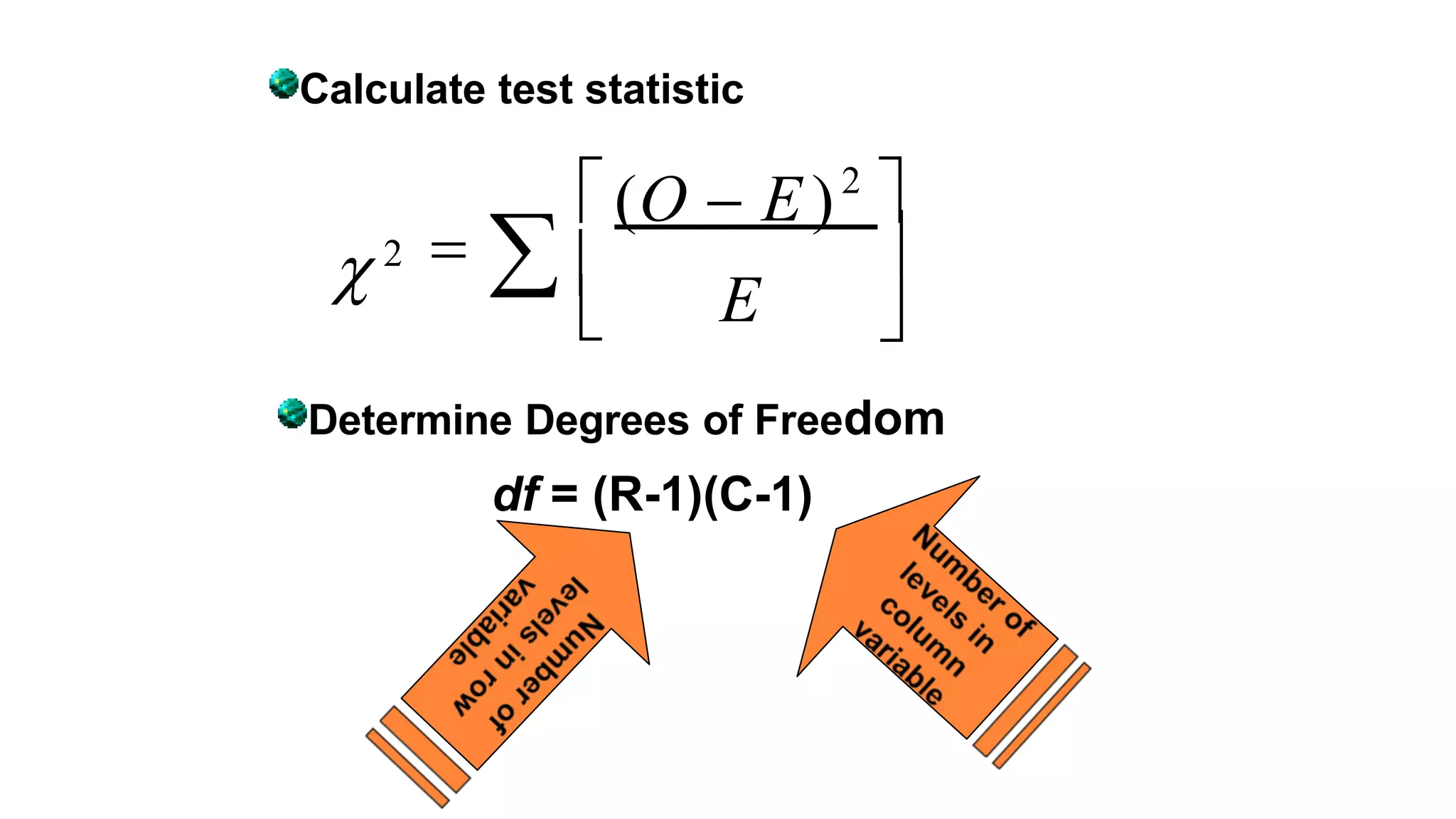
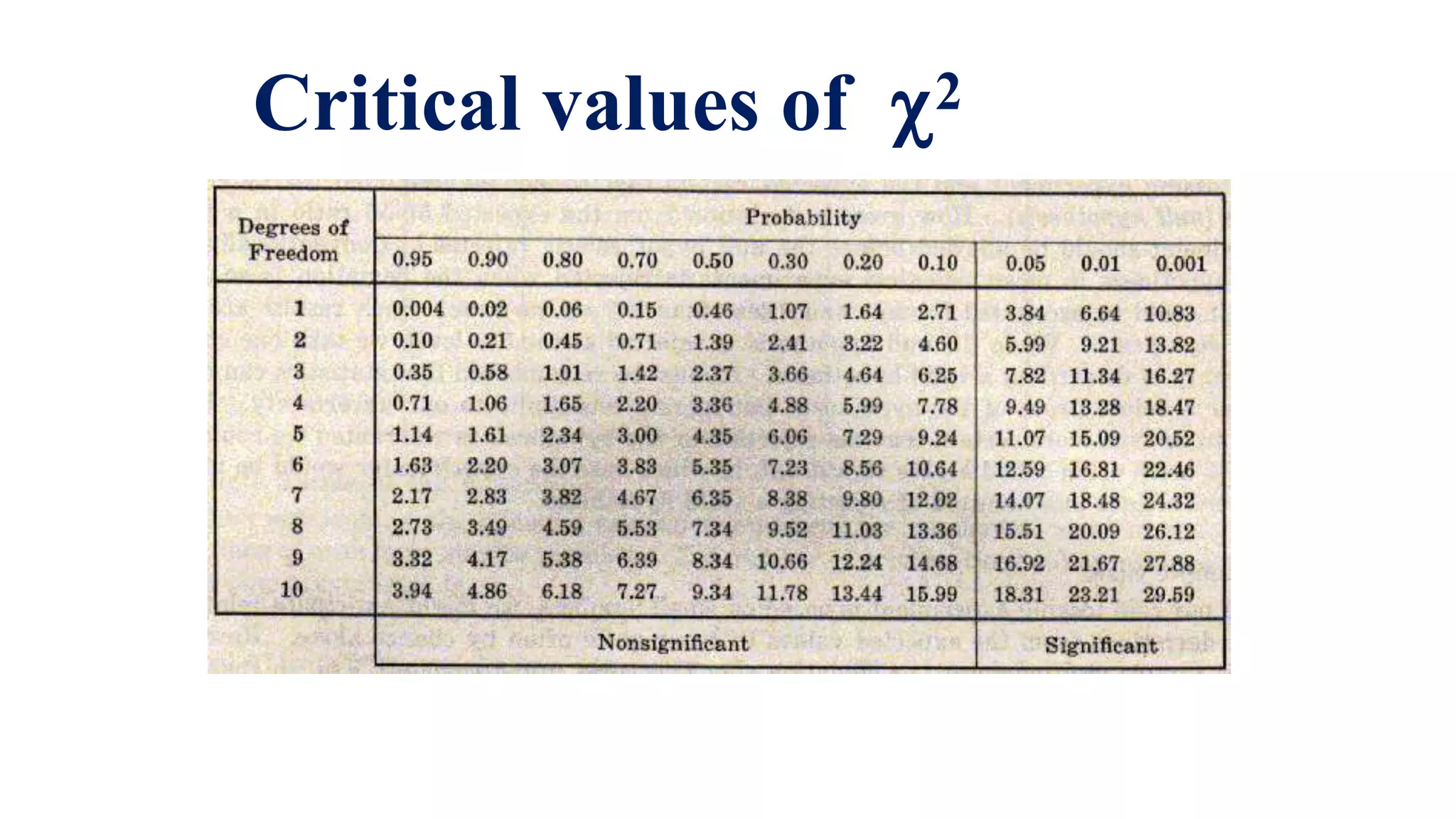
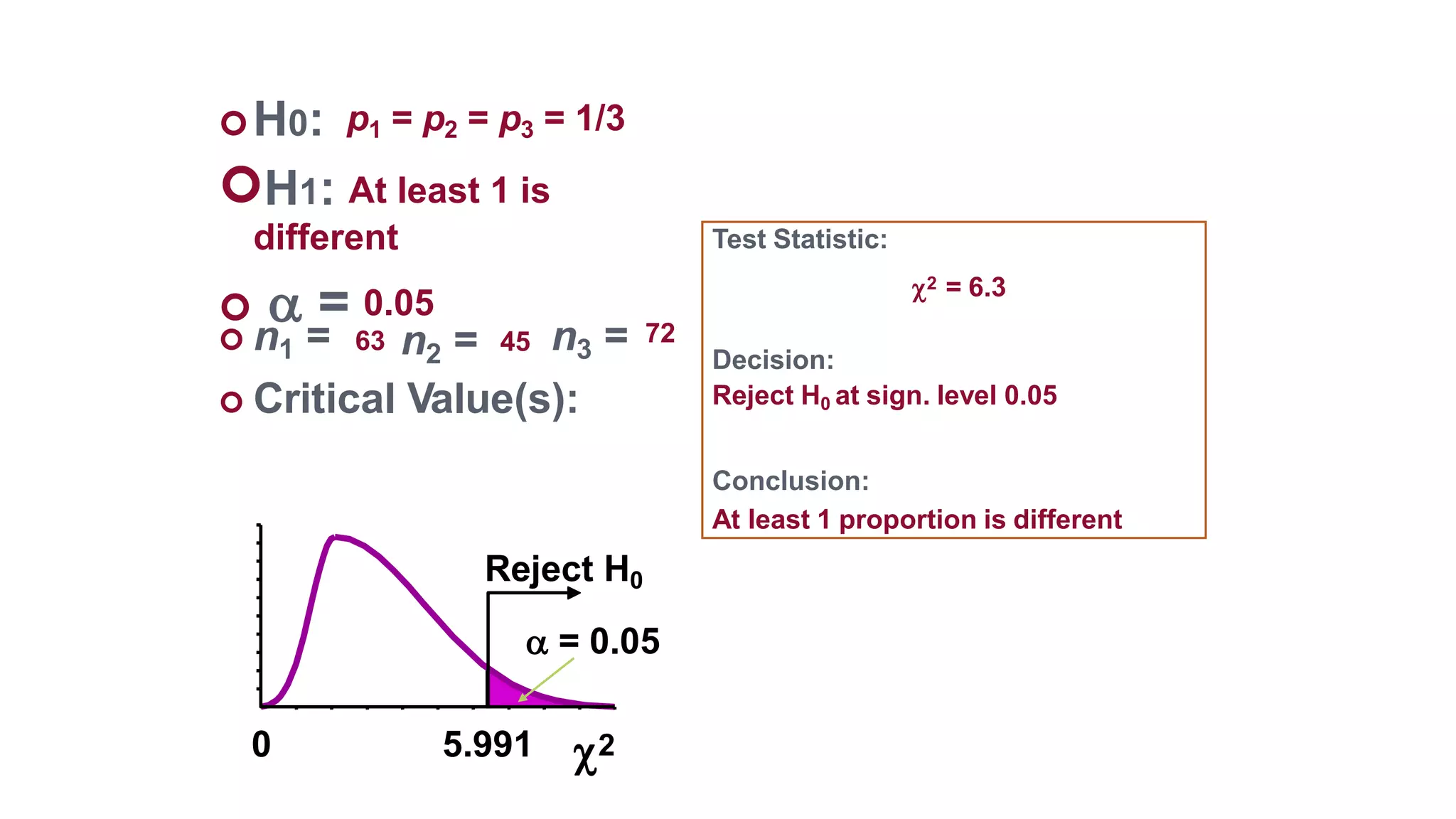
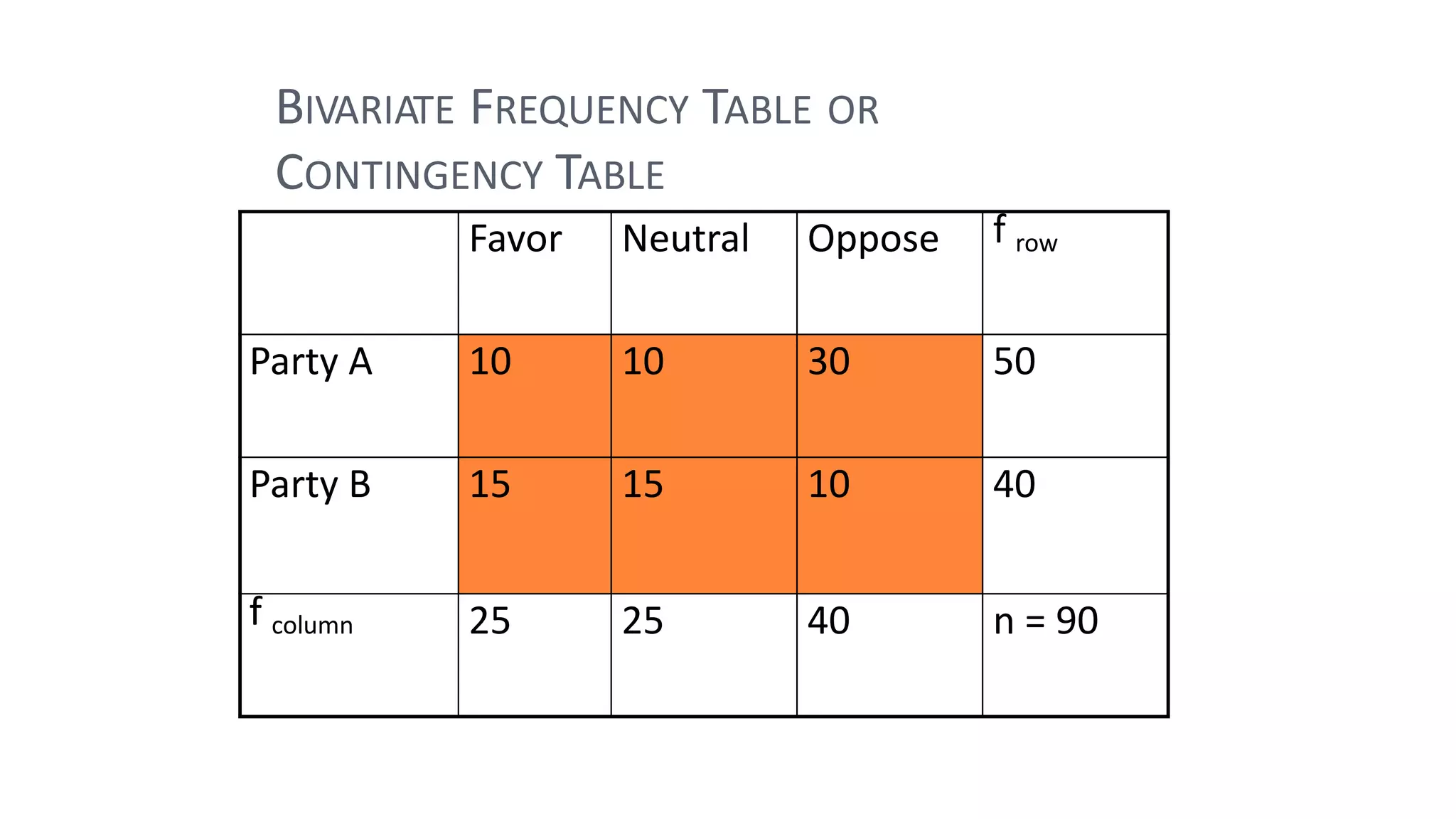
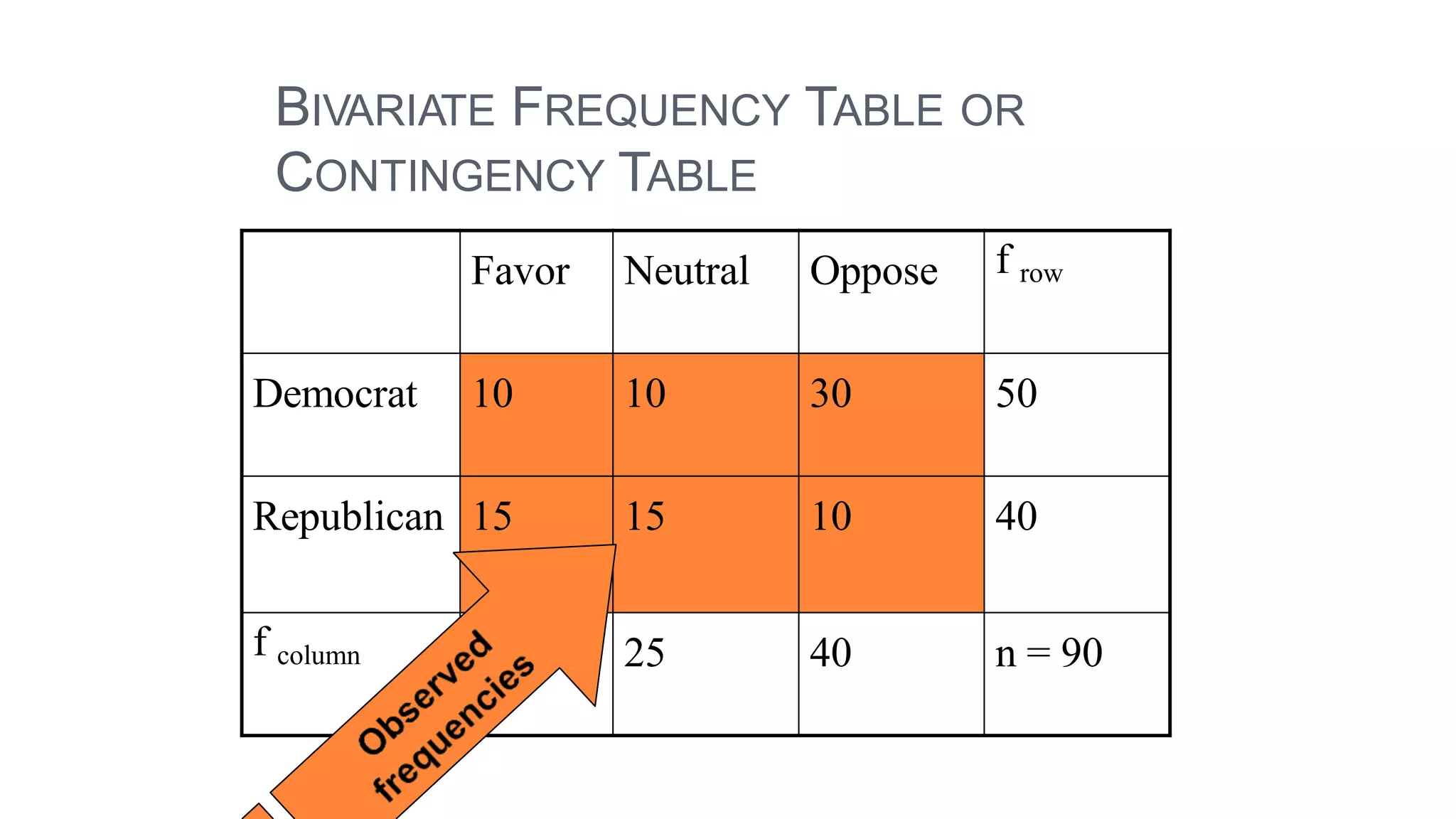
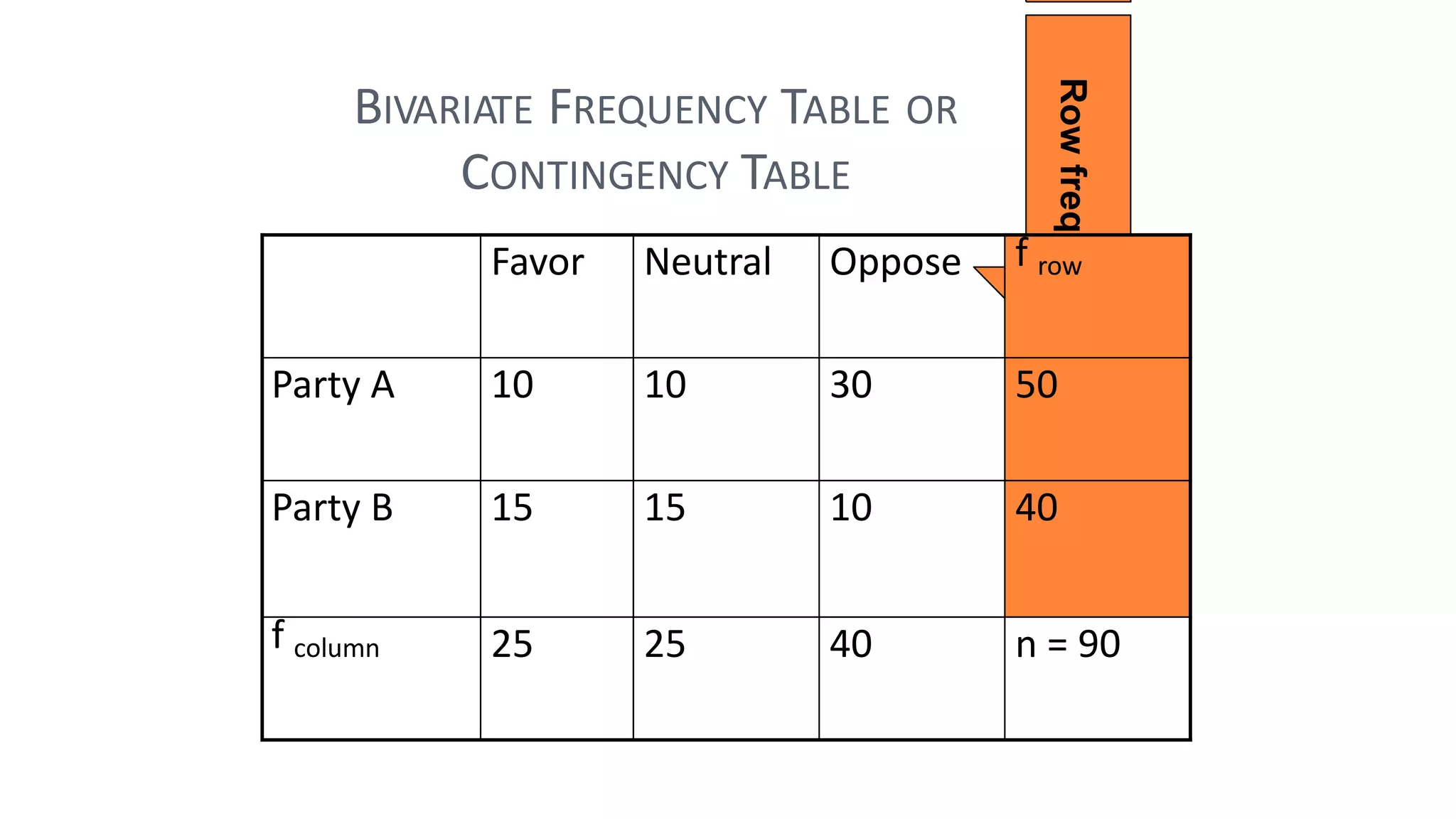
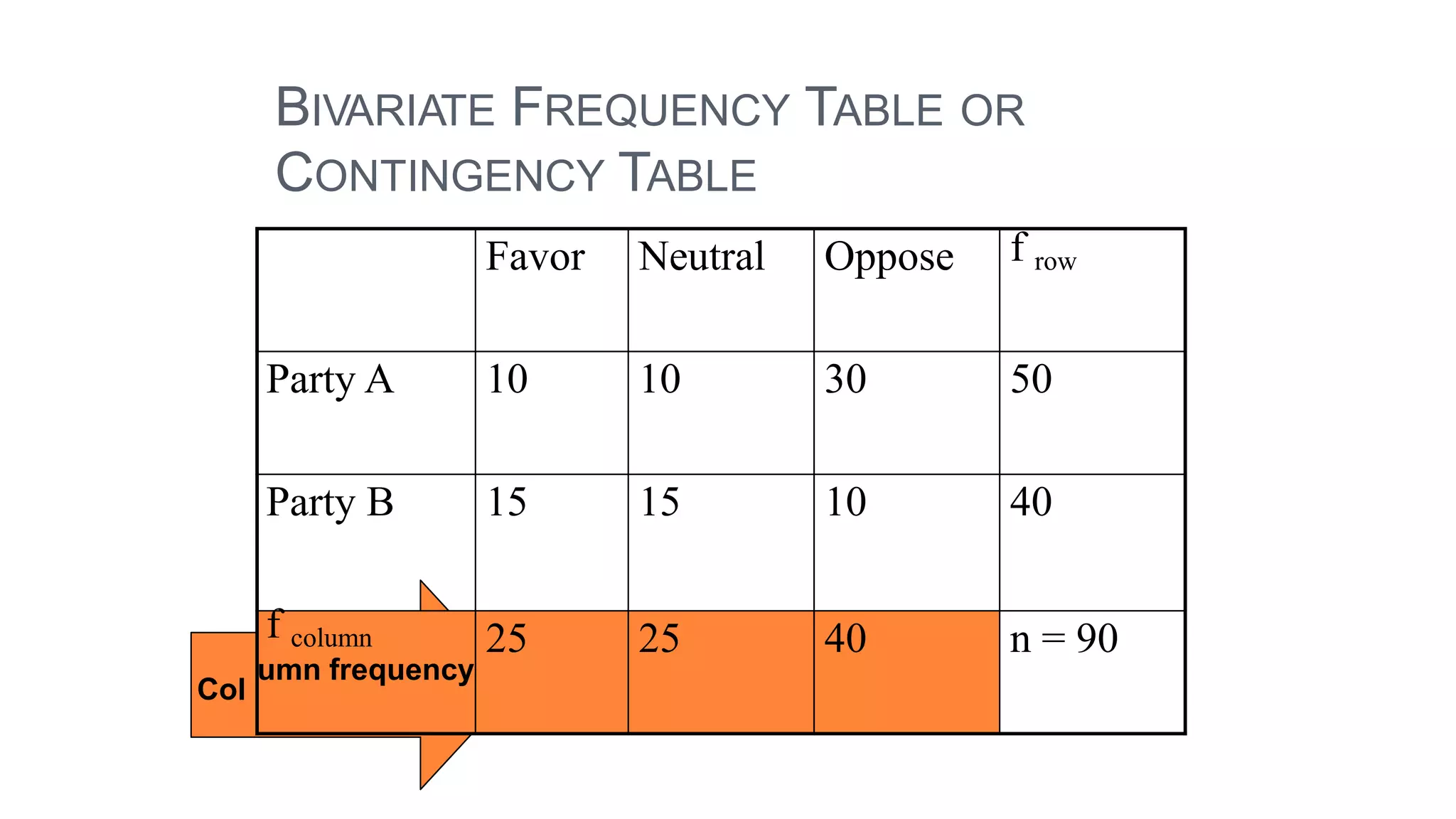
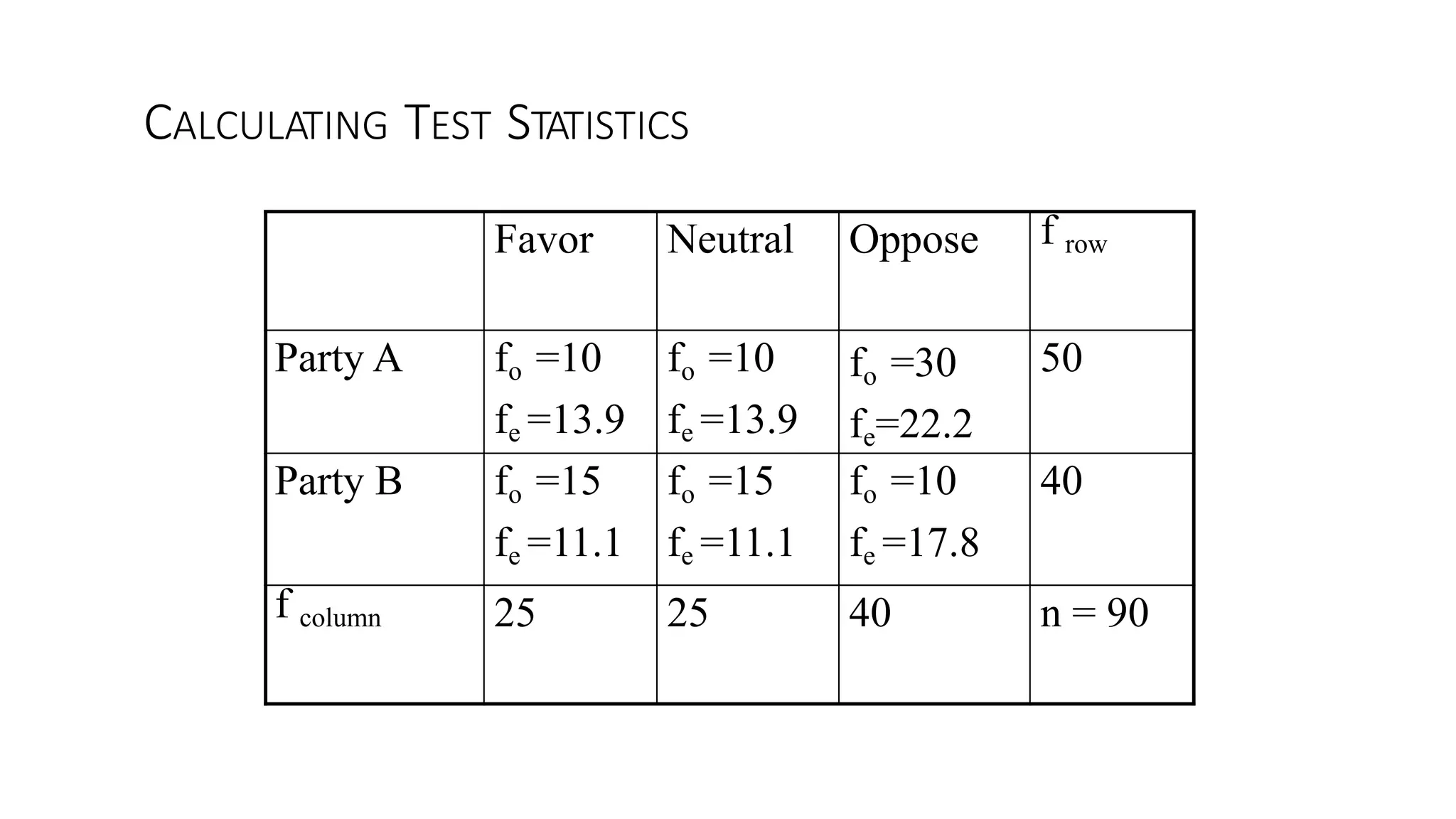
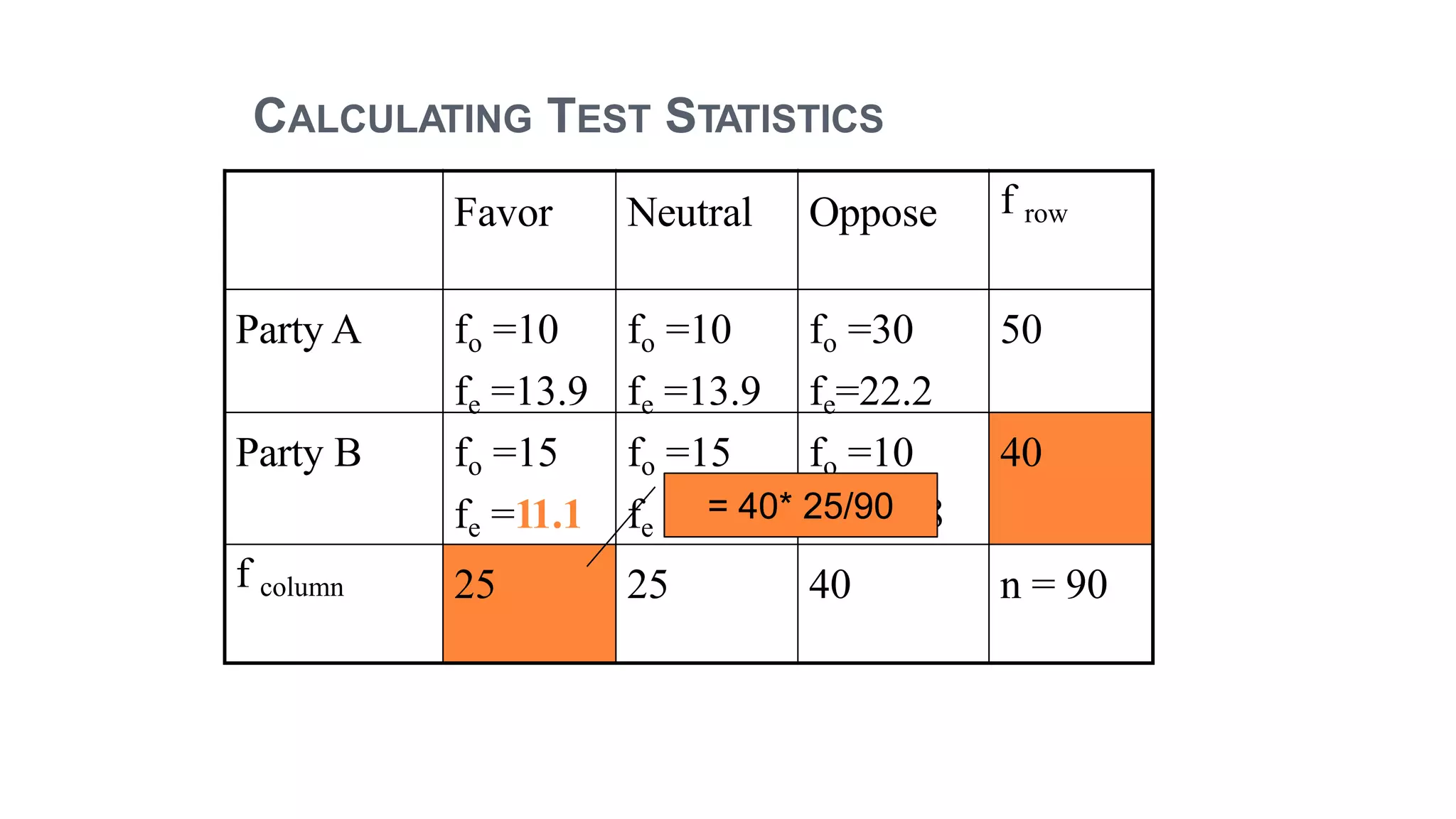
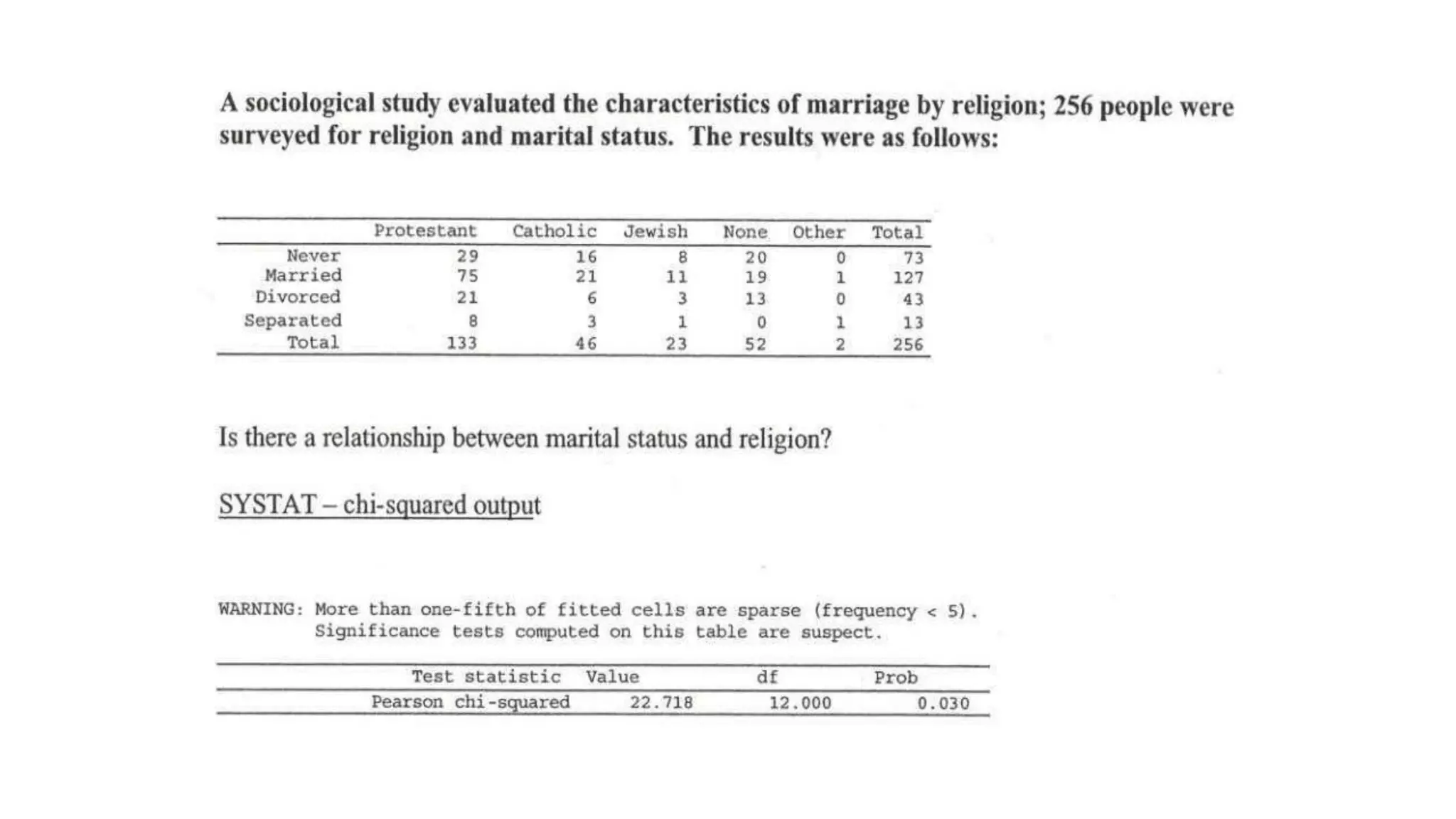
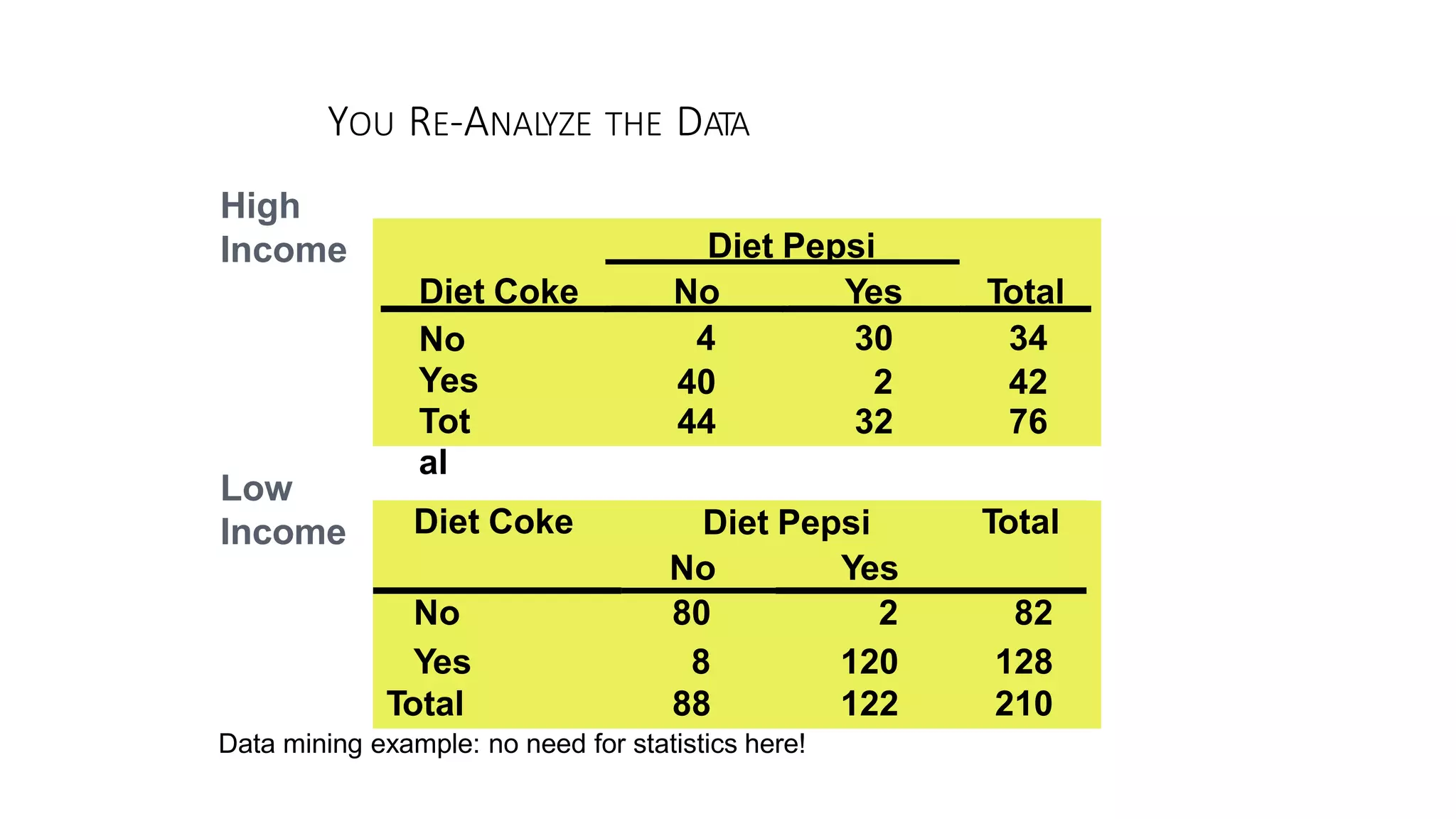
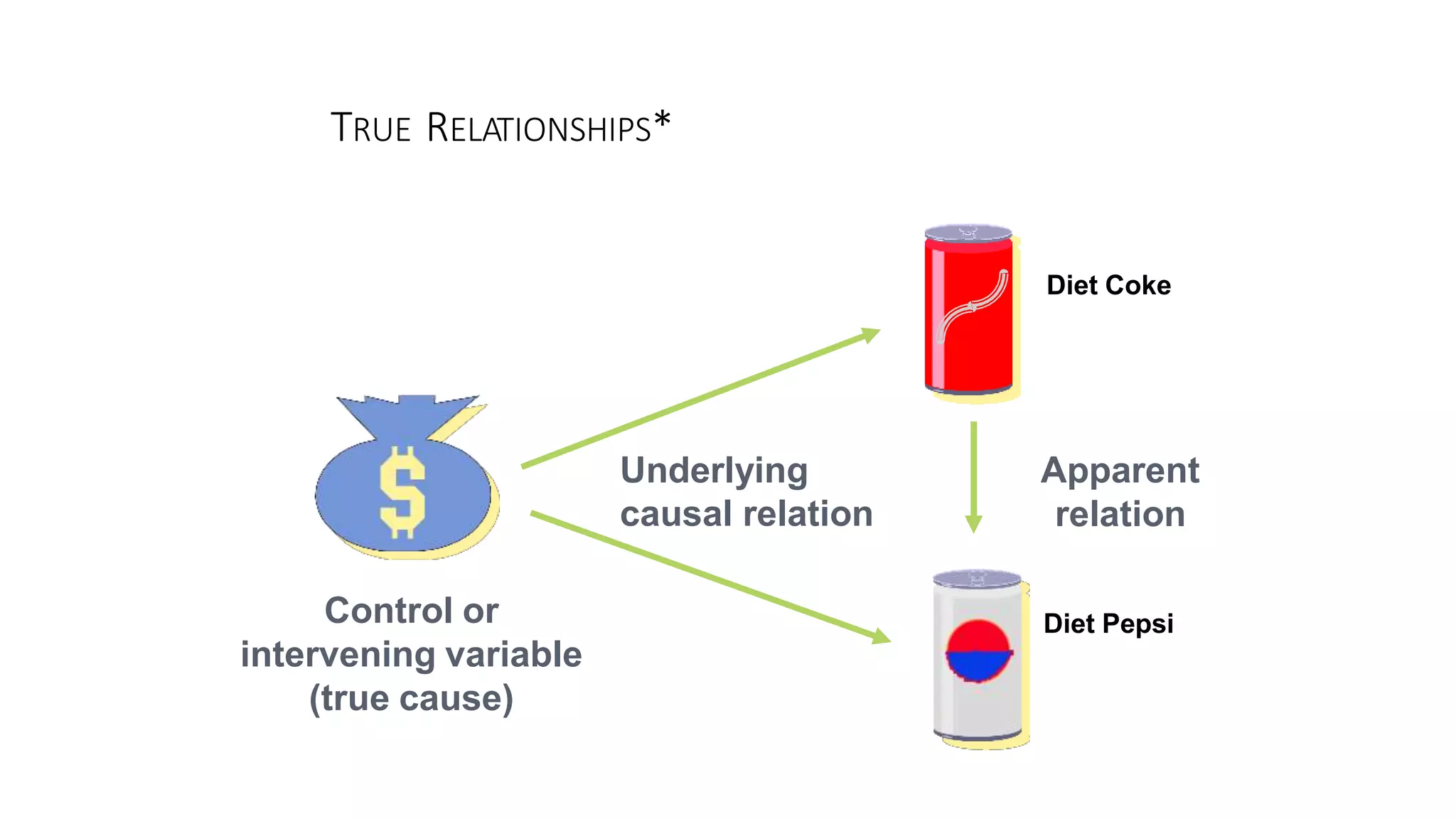
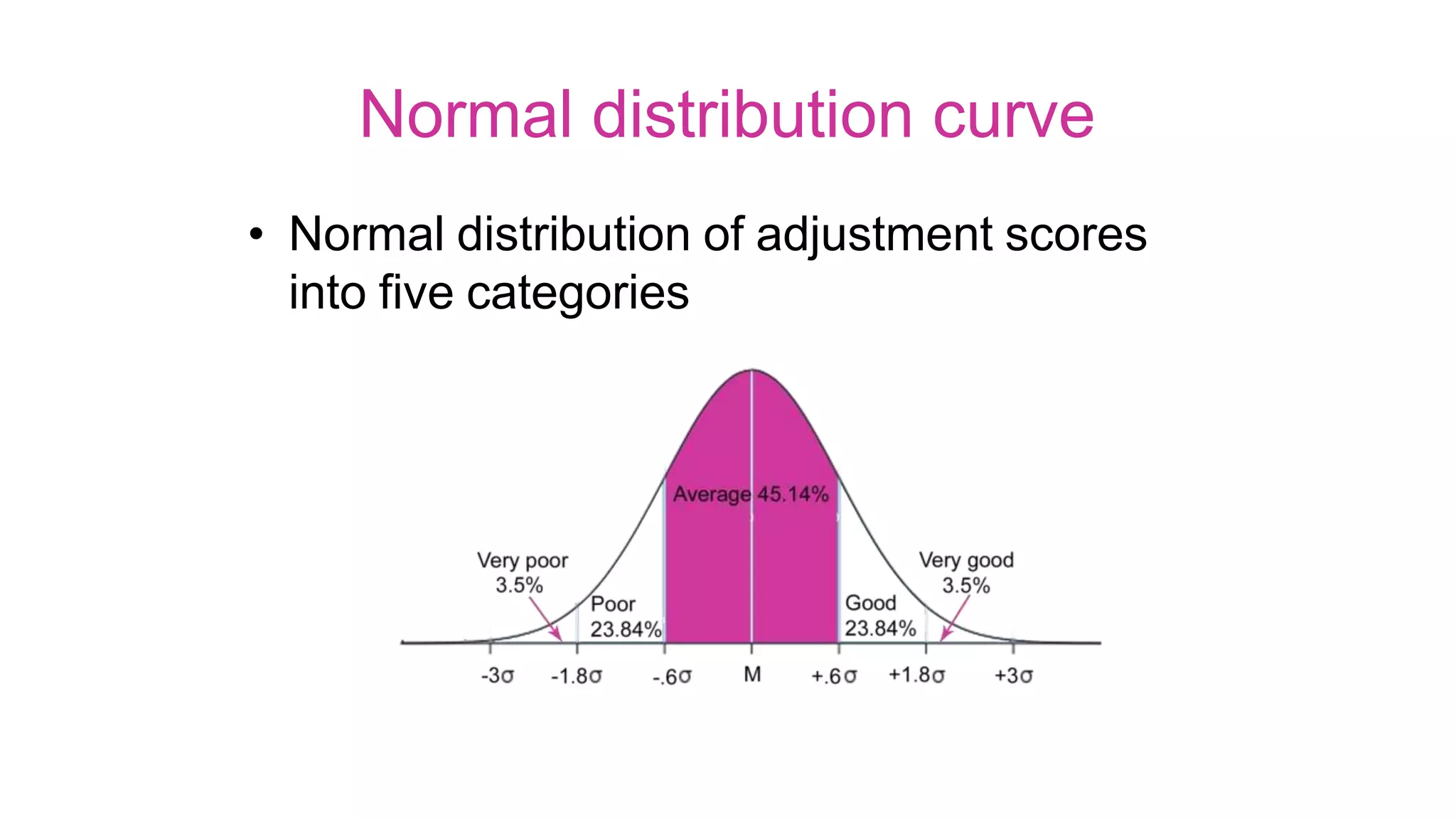
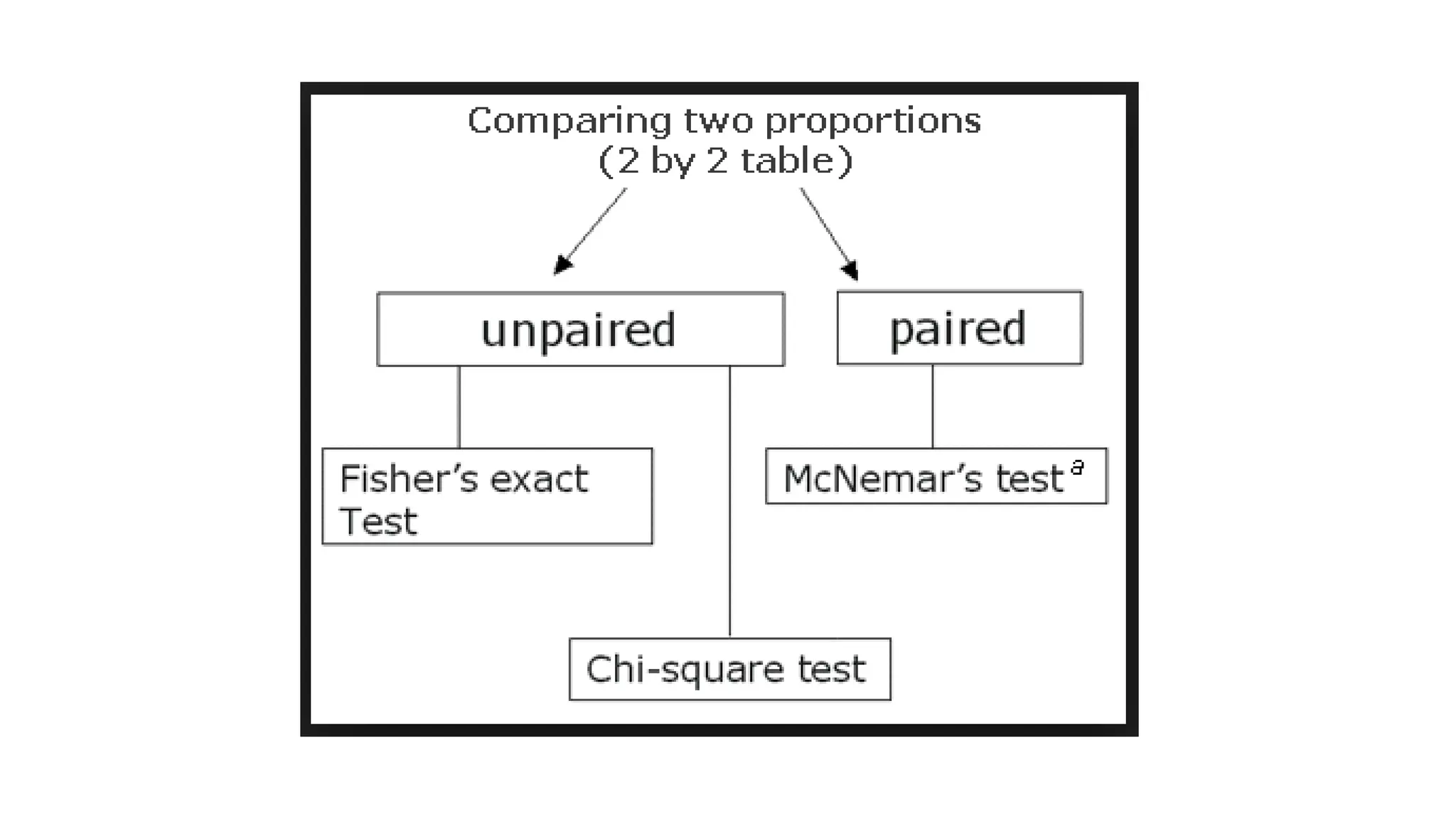
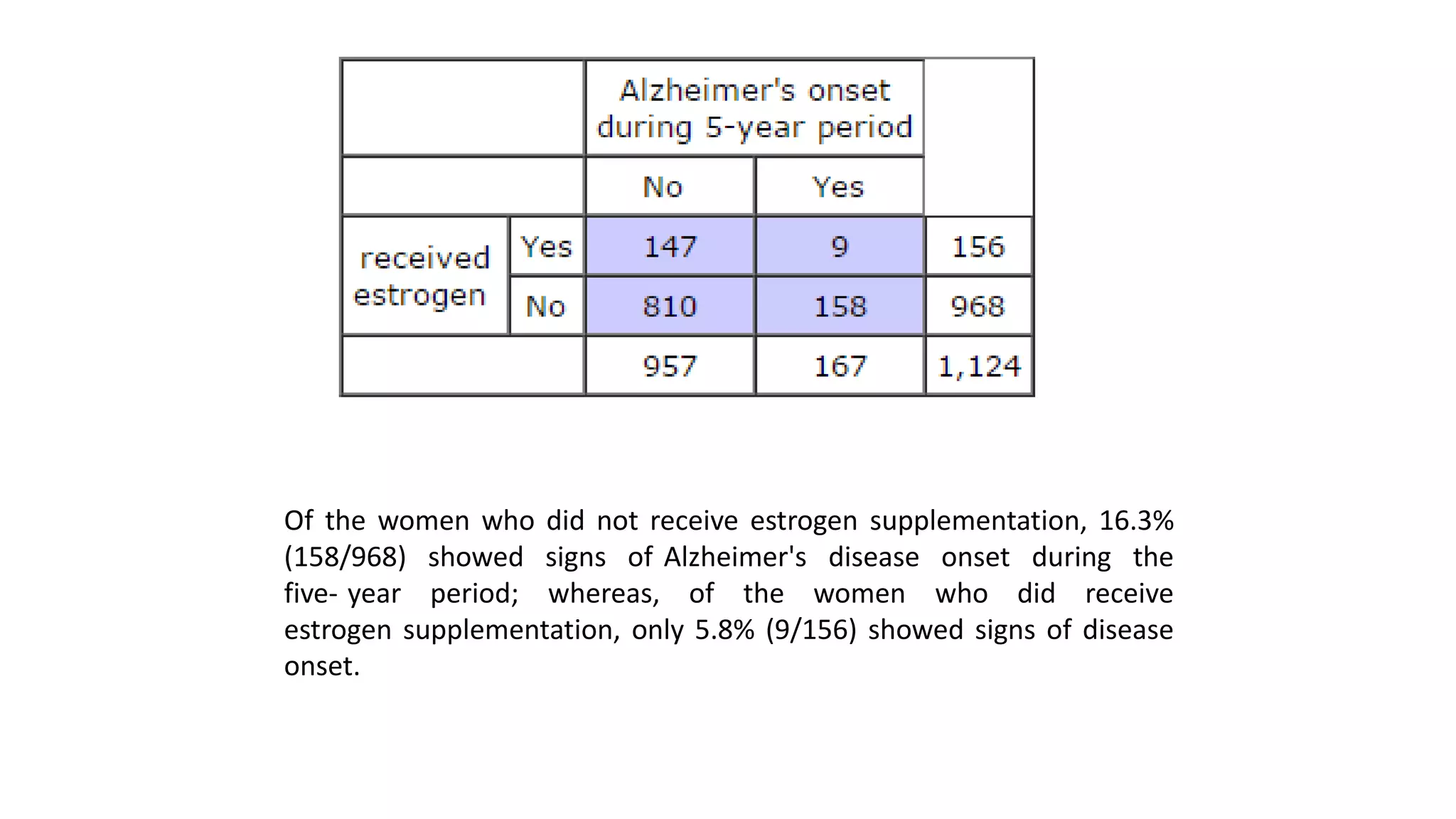
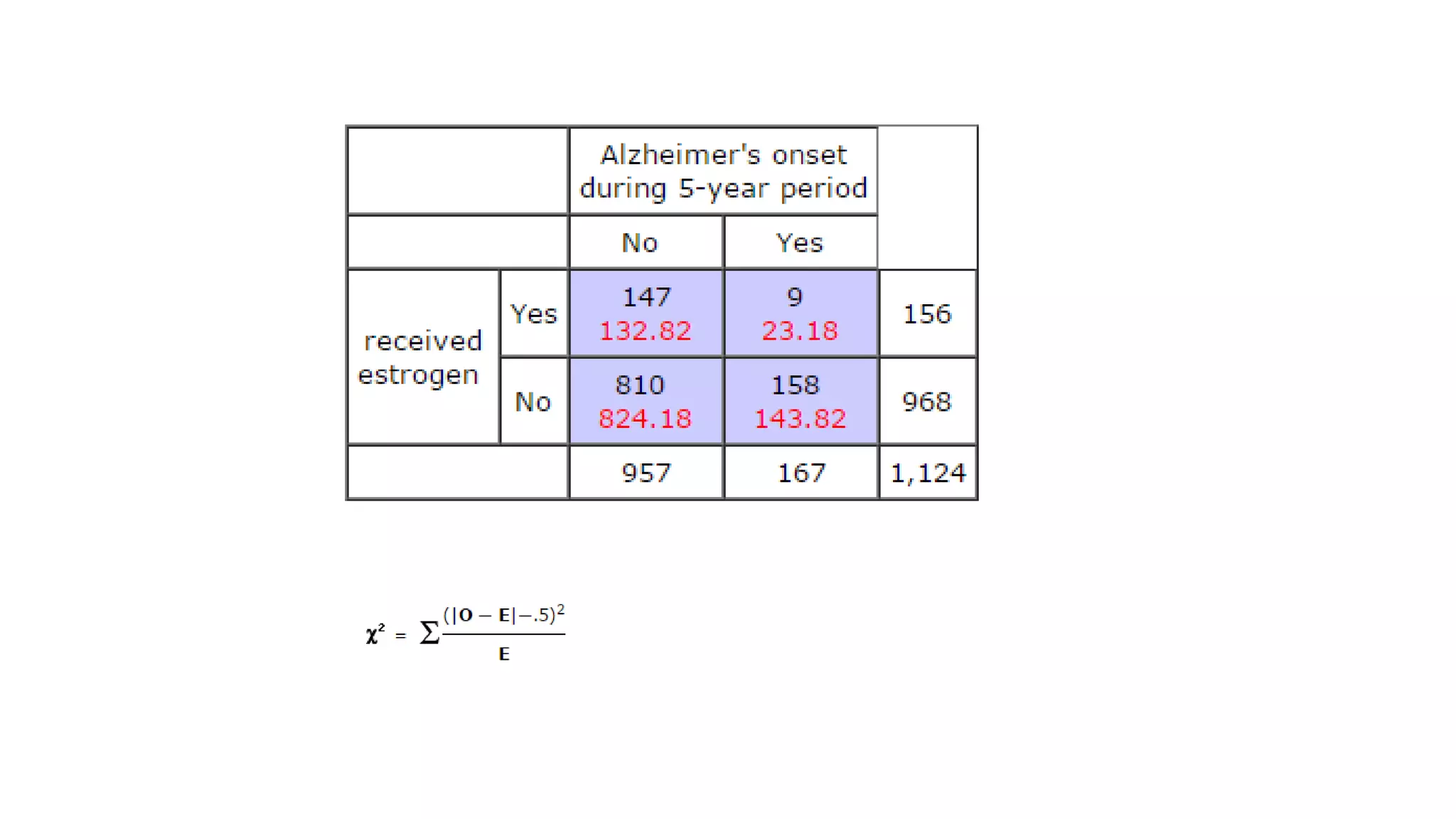
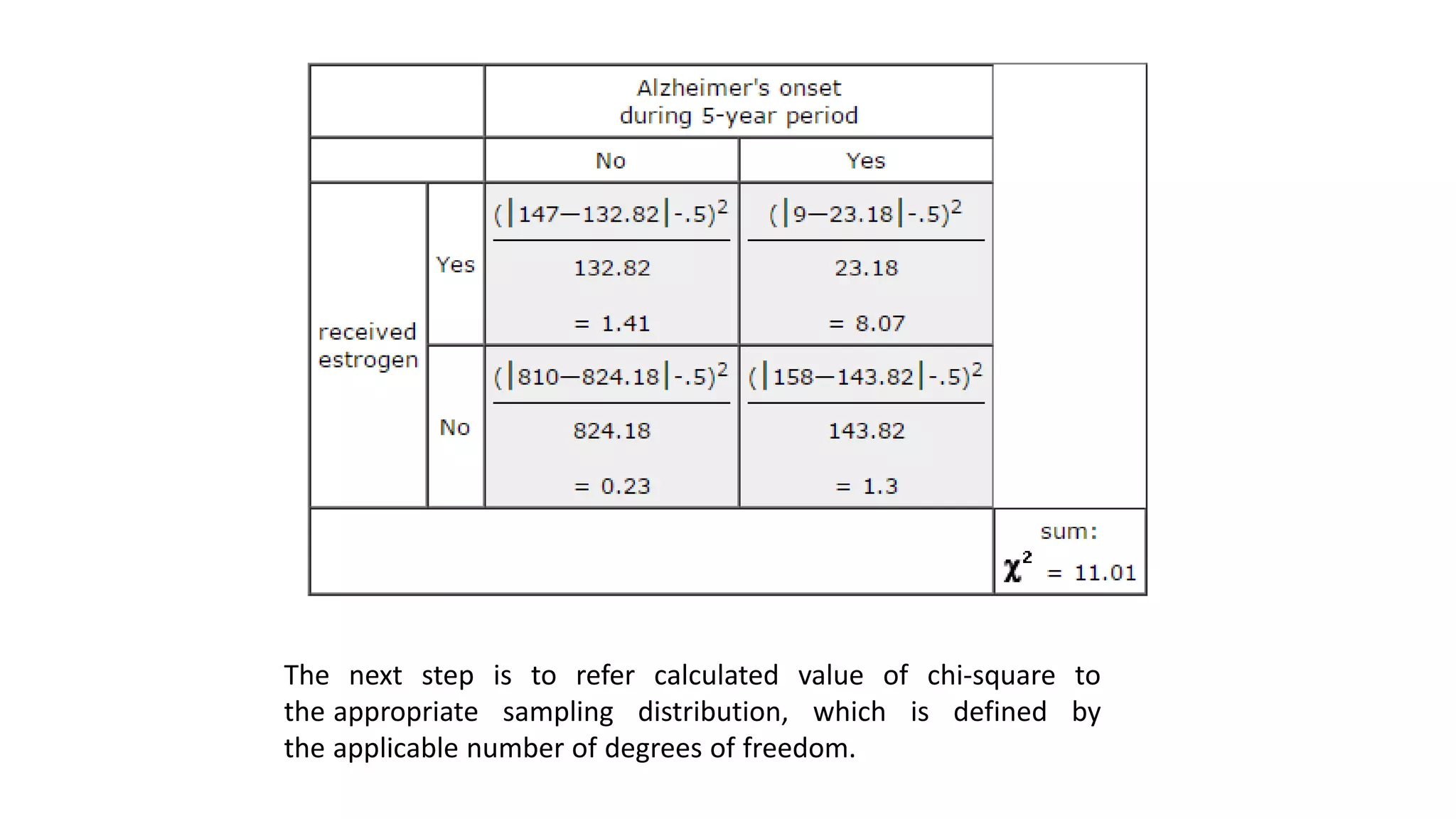
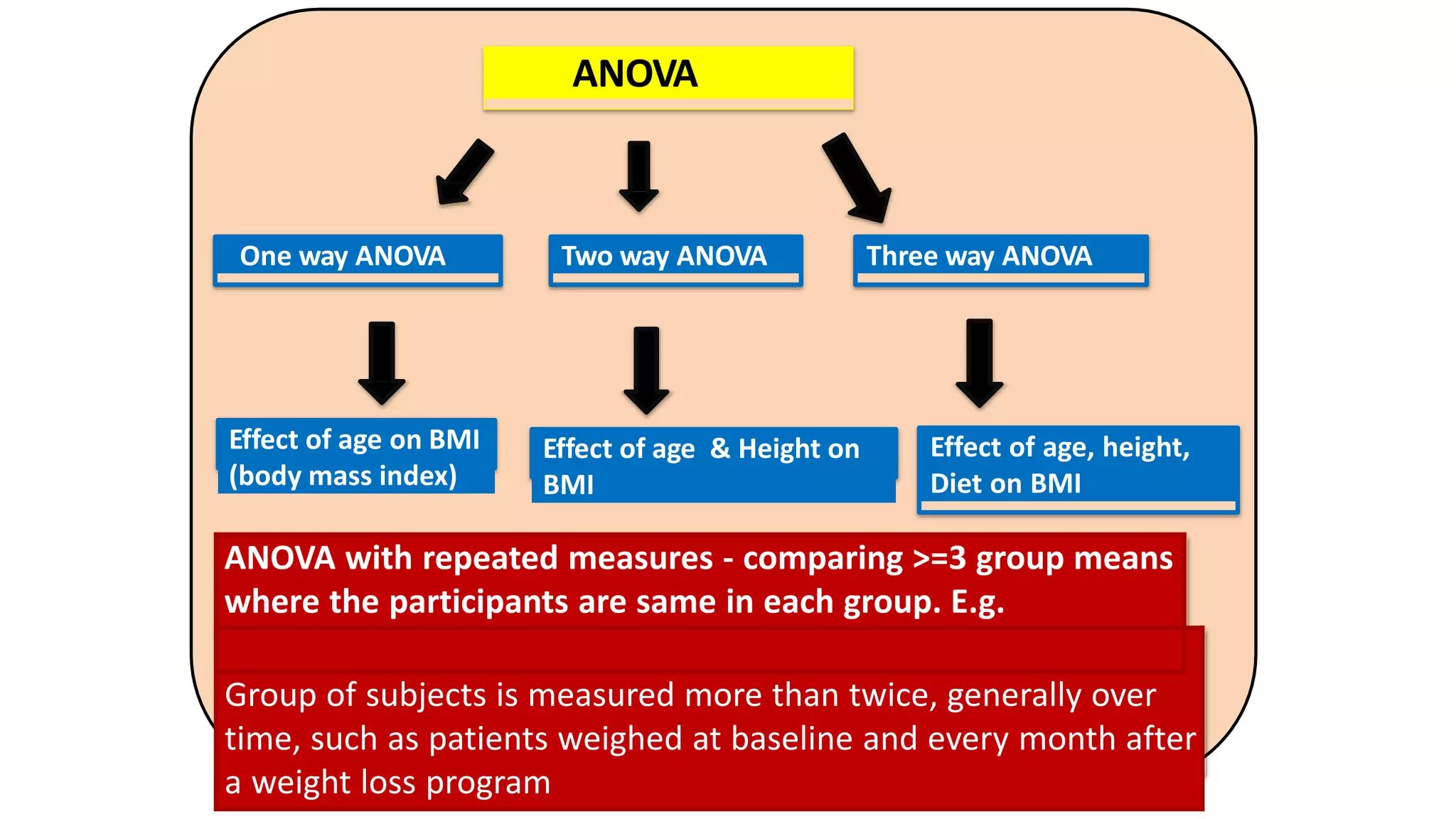
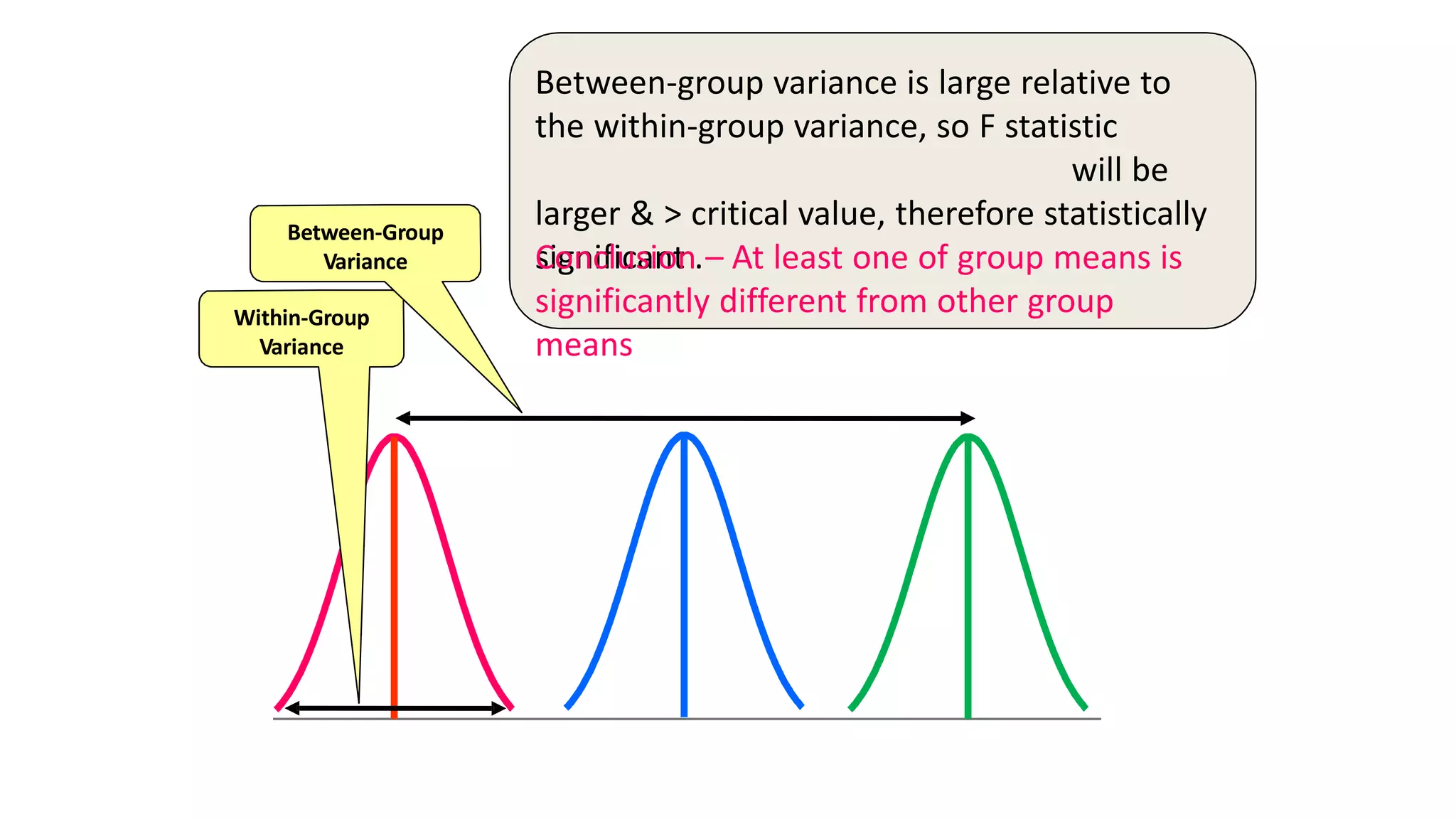
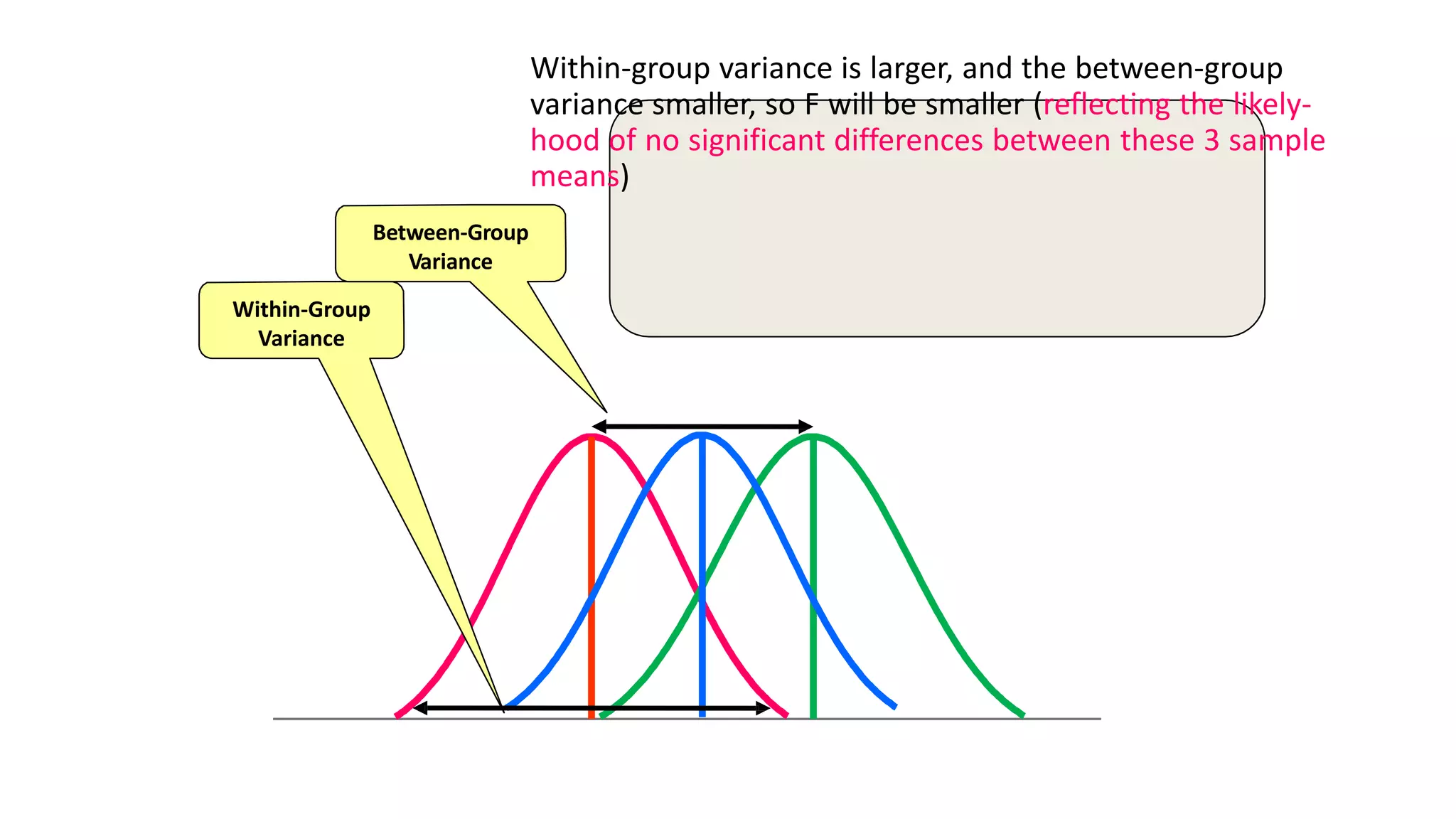
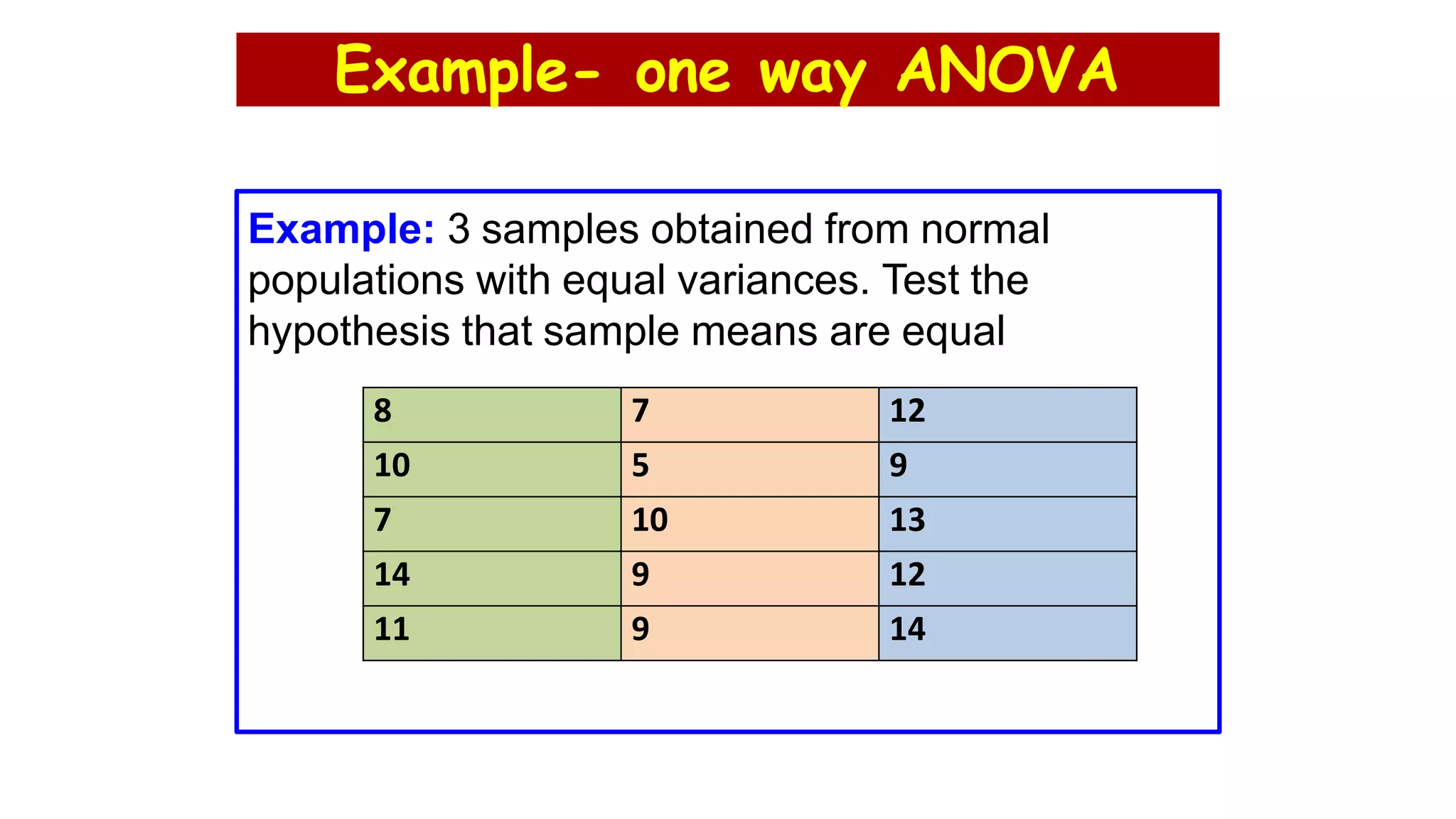
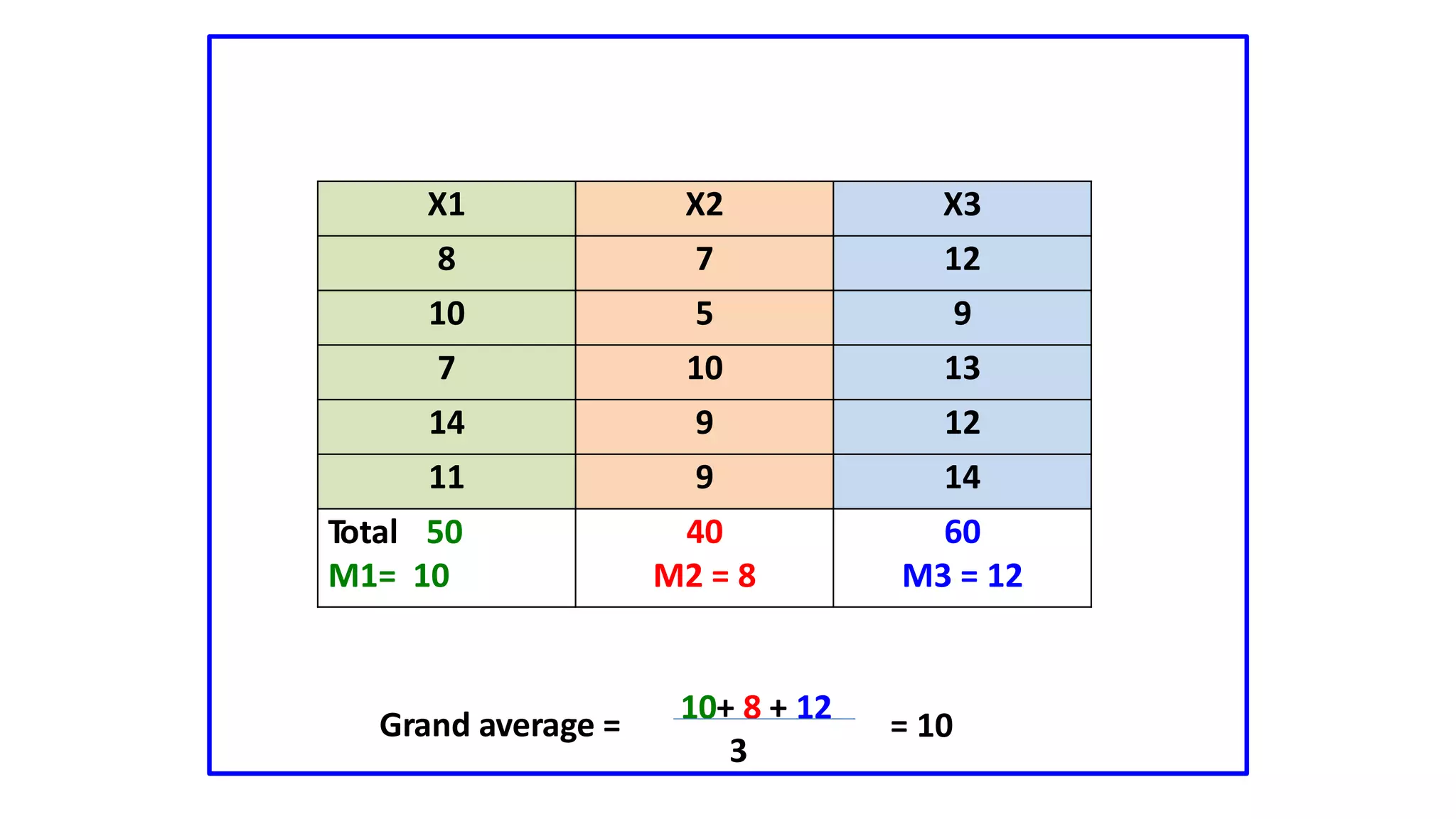
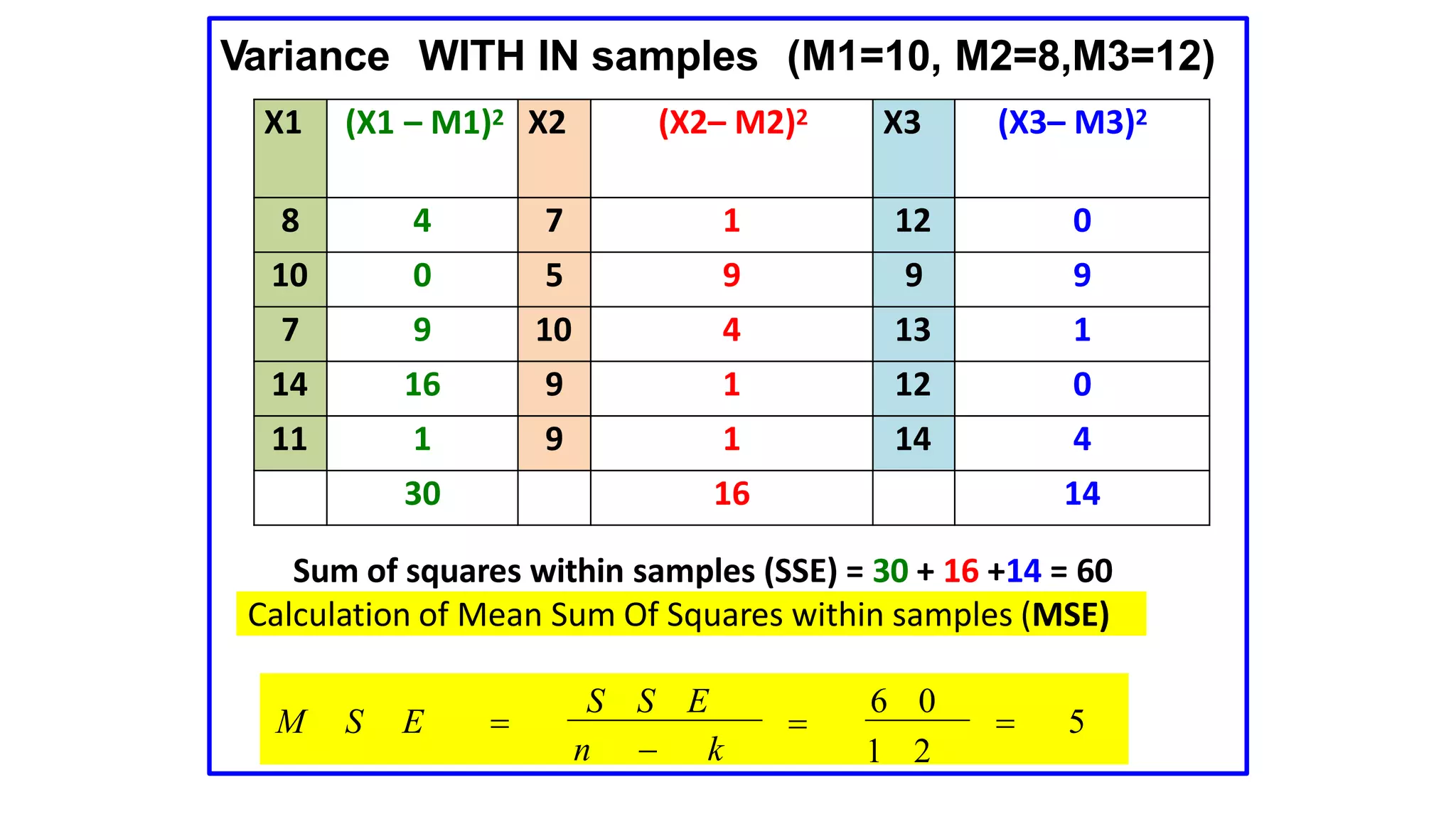
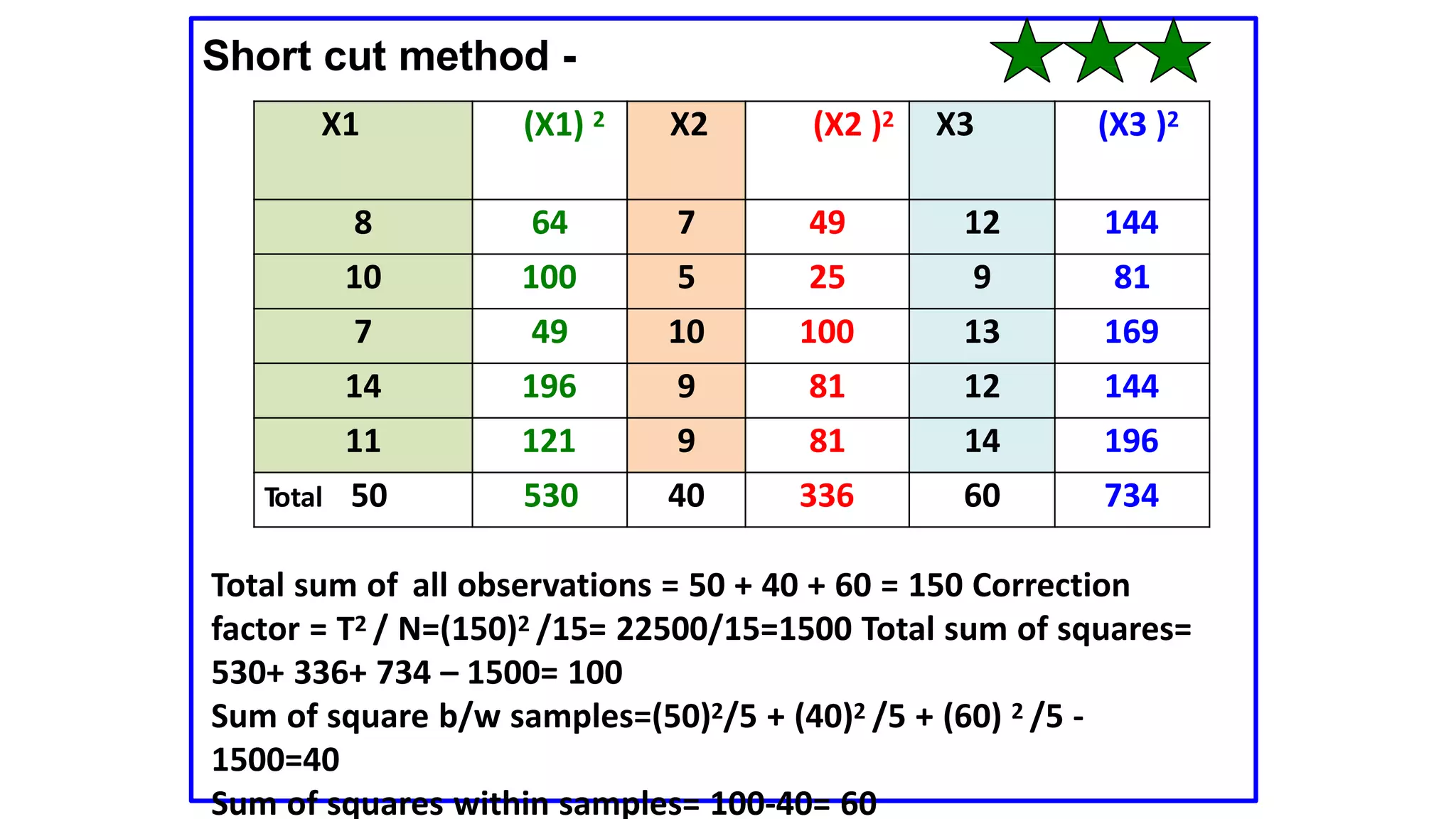
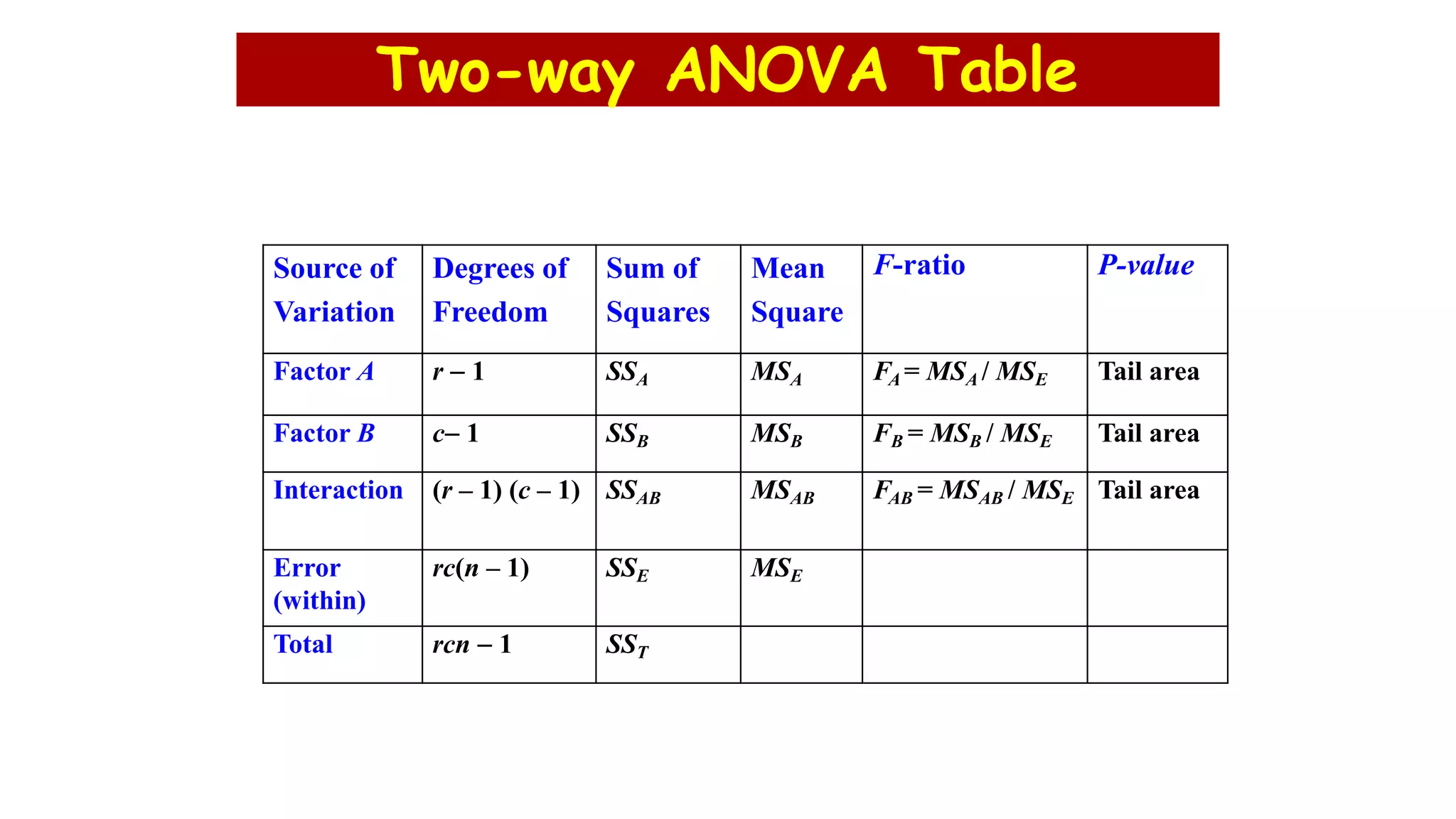
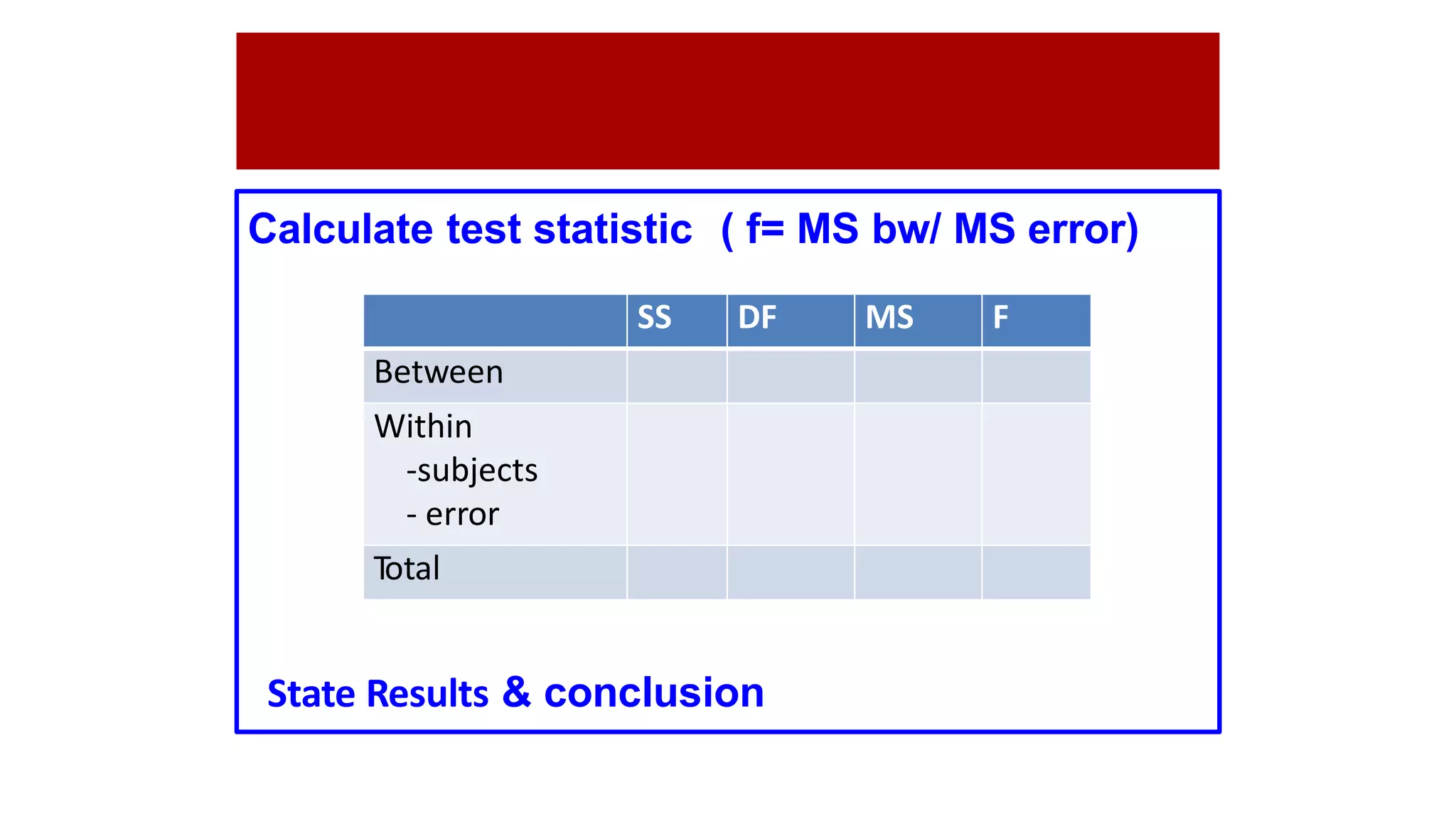
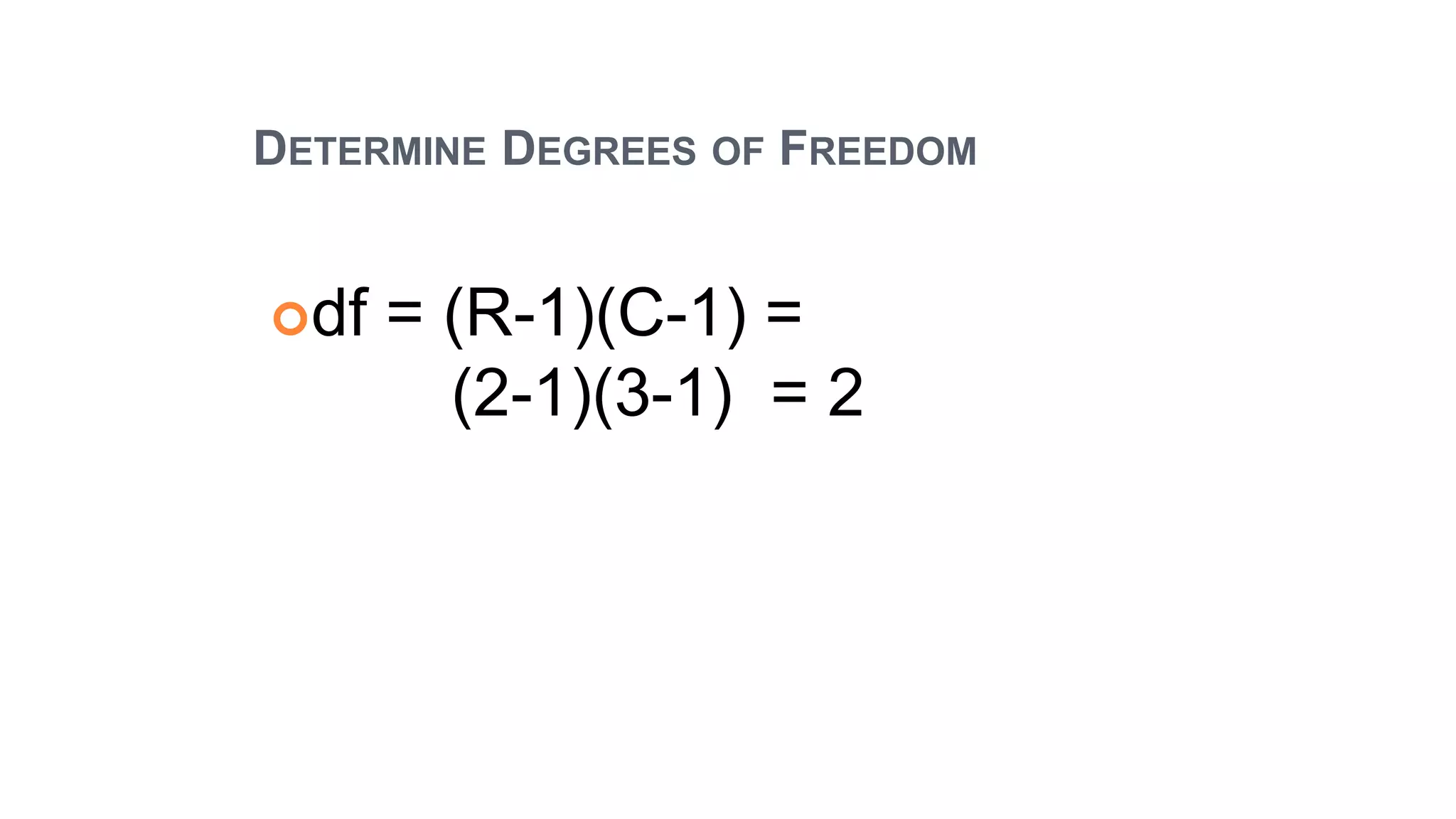The document discusses hypothesis testing using parametric and non-parametric tests. It defines key concepts like the null and alternative hypotheses, type I and type II errors, and p-values. Parametric tests like the t-test, ANOVA, and Pearson's correlation assume the data follows a particular distribution like normal. Non-parametric tests like the Wilcoxon, Mann-Whitney, and chi-square tests make fewer assumptions and can be used when sample sizes are small or the data violates assumptions of parametric tests. Examples are provided of when to use parametric or non-parametric tests depending on the type of data and statistical test being performed.