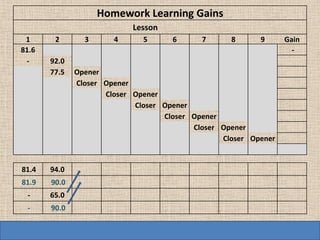
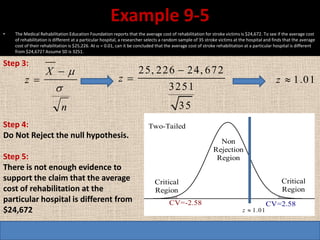
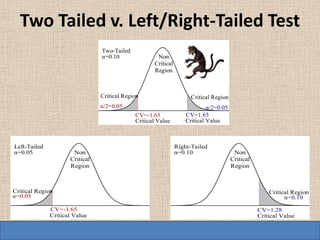
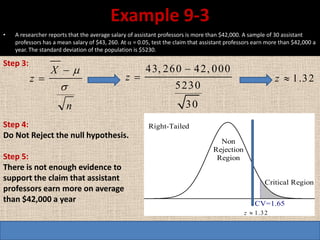
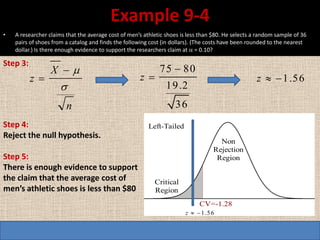
Here are the steps to solve this problem: 1. State the hypotheses: H0: μ = 100 H1: μ ≠ 100 2. The critical values are ±1.96 (two-tailed test, α=0.05) 3. Compute the test statistic: z = (140 - 100)/15/√40 = 20/15/2 = 4 4. The test statistic is in the critical region, so reject the null hypothesis. 5. There is strong evidence that the medication affected intelligence since the sample mean is much higher than the population mean.

1. OPENER
Please find the critical value(s) for each
situation and draw the appropriate
figure, showing the critical region:
a. Two-Tailed Test α=0.05
b. Right-Tailed Test α=0.02
c. Left-Tailed Test α=0.01

2. Homework Learning Gains
Lesson
1 2 3 4 5 6 7 8 9 Gain
81.6 -
- 92.0
77.5 Opener
Closer Opener
Closer Opener
Closer Opener
Closer Opener
Closer Opener
Closer Opener
81.4 94.0
81.9 90.0
- 65.0
- 90.0

3. Speaking of Homework / Grades
• Check Edbox
• Not everyone has handed in their
homework calendars for Ch. 8
• Barring any discussed changes to
your grade, what you see on Edbox
is an accurate reflection of what will
go home with your quarter grades.

4. Review
• A statistical test uses the data
obtained from a sample to make a
decision about whether the null
hypothesis should be rejected.
• The numerical value obtained from a
statistical test is called the test value.

5. Review
• The critical value separates the
critical region from the noncritical
region.
• The critical region is the range of
values of the test value that indicates
that there is a significant difference
and that the null hypothesis should
be rejected.

6. Two Tailed v. Left/Right-Tailed Test
Two-Tailed
α=0.10 Non
Critical
Region
Critical Region Critical Region
α/2=0.05 α/2=0.05
CV=-1.65 CV=1.65
Critical Value Critical Value
Left-Tailed Right-Tailed
α=0.05 Non α=0.10 Non
Critical Critical
Region Region
Critical Region Critical Region
α=0.05 α=0.10
CV=-1.65 CV=1.28
Critical Value Critical Value

7. Five Steps in Hypothesis Testing
1. State the hypotheses and identify the claim.
Make sure to use proper symbols.
Please include proper units when given.
2. Find the critical value(s).
Include a diagram that displays all the pertinent information.
3. Compute the test value.
Include the proper formula.
Round properly.
Locate and place test value on the diagram.
4. Make the decision to reject or not to reject the null hypothesis.
Use a complete sentence.
5. Summarize the result.
Use complete sentence(s) that states the final conclusion clearly in the context of
the problem.
Use the proper vocabulary and statistical terms.
Include the proper units if they are given.

8. Section 9-3
Z-Test for a Mean

9. When to Use the z Test
• The z test is a statistical test for
the mean of a population. It can
be used when n> 30 or when the
population is normally distributed
and σ is known.

10. Formula for the z Test
X 
z

n

11. Hypothesis Testing
Traditional Method

12. Example 9-3
• A researcher reports that the average salary of assistant
professors is more than $42,000. A sample of 30 assistant
professors has a mean salary of $43, 260. At  = 0.05, test
the claim that assistant professors earn more than $42,000
a year. The standard deviation of the population is $5230.
Non
Rejection
Region
H0: µ≤$42,000
H1: µ>$42,000 (Claim)

13. Example 9-3
• A researcher reports that the average salary of assistant professors is more than $42,000. A sample of 30 assistant
professors has a mean salary of $43, 260. At  = 0.05, test the claim that assistant professors earn more than $42,000 a
year. The standard deviation of the population is $5230.
Step 3:
X  4 3, 2 6 0  4 2, 0 0 0
z z  z  1 .3 2
 5230
n 30
Step 4: Right-Tailed
Do Not Reject the null hypothesis.
Non
Rejection
Step 5: Region
There is not enough evidence to
support the claim that assistant Critical Region
professors earn more on average
than $42,000 a year CV=1.65
z  1 .3 2

14. Example 9-4
• A researcher claims that the average cost of men’s athletic
shoes is less than $80. He selects a random sample of 36 pairs
of shoes from a catalog and finds the following cost (in dollars).
(The costs have been rounded to the nearest dollar.) Is there
enough evidence to support the researchers claim at  = 0.10?
Reference Page 351 for costs.
Non
Rejection
Region
H0: µ≥$80
H1: µ<$80 (Claim)

15. Example 9-4
• A researcher claims that the average cost of men’s athletic shoes is less than $80. He selects a random sample of 36
pairs of shoes from a catalog and finds the following cost (in dollars). (The costs have been rounded to the nearest
dollar.) Is there enough evidence to support the researchers claim at  = 0.10?
Step 3:
X  75  80
z z  z   1 .5 6
 19.2
n 36
Step 4: Left-Tailed
Reject the null hypothesis.
Non
Rejection
Step 5: Region
There is enough evidence to support
the claim that the average cost of Critical
men’s athletic shoes is less than $80 Region
CV=-1.28
z   1 .5 6

16. Example 9-5
• The Medical Rehabilitation Education Foundation reports
that the average cost of rehabilitation for stroke victims is
$24,672. To see if the average cost of rehabilitation is
different at a particular hospital, a researcher selects a
random sample of 35 stroke victims at the hospital and
finds that the average cost of their rehabilitation is
$25,226. At  = 0.01, can it be concluded that the average
cost of stroke rehabilitation at a particular hospital is
different from $24,672? Assume SD is 3251.

17. Example 9-5
• The Medical Rehabilitation Education Foundation reports that the average cost of rehabilitation for stroke victims is $24,672. To see if the average cost
of rehabilitation is different at a particular hospital, a researcher selects a random sample of 35 stroke victims at the hospital and finds that the average
cost of their rehabilitation is $25,226. At  = 0.01, can it be concluded that the average cost of stroke rehabilitation at a particular hospital is different
from $24,672? Assume SD is 3251.
Step 3:
X  2 5, 2 2 6  2 4, 6 7 2
z z  z  1 .0 1
 3251
n 35
Step 4: Two-Tailed
Do Not Reject the null hypothesis.
Non
Rejection
Step 5: Region
There is not enough evidence to
support the claim that the average Critical Critical
cost of rehabilitation at the Region Region
particular hospital is different from CV=-2.58 CV=2.58
$24,672 z  1.01

18. Five Steps in Hypothesis Testing
1. State the hypotheses and identify the claim.
Make sure to use proper symbols.
Please include proper units when given.
2. Find the critical value(s).
Include a diagram that displays all the pertinent information.
3. Compute the test value.
Include the proper formula.
Round properly.
Locate and place test value on the diagram.
4. Make the decision to reject or not to reject the null hypothesis.
Use a complete sentence.
5. Summarize the result.
Use complete sentence(s) that states the final conclusion clearly in the context of
the problem.
Use the proper vocabulary and statistical terms.
Include the proper units if they are given.

19. Your Moment of Zen

20. HOMEWORK
Read Section 9-3
Pg. 358: 14-20all
Assigned: 2012.04.11
Due: 2012.04.16
Please write this on your Calendar

21. CLOSER
In the population, the average IQ is 100
with a standard deviation of 15. A team of
scientists wants to test a new medication
to see if it has an effect on intelligence (as
measured by IQ). A sample of 40
participants who have taken the
medication has a mean of 140. Did the
medication affect intelligence? Use α=0.05.