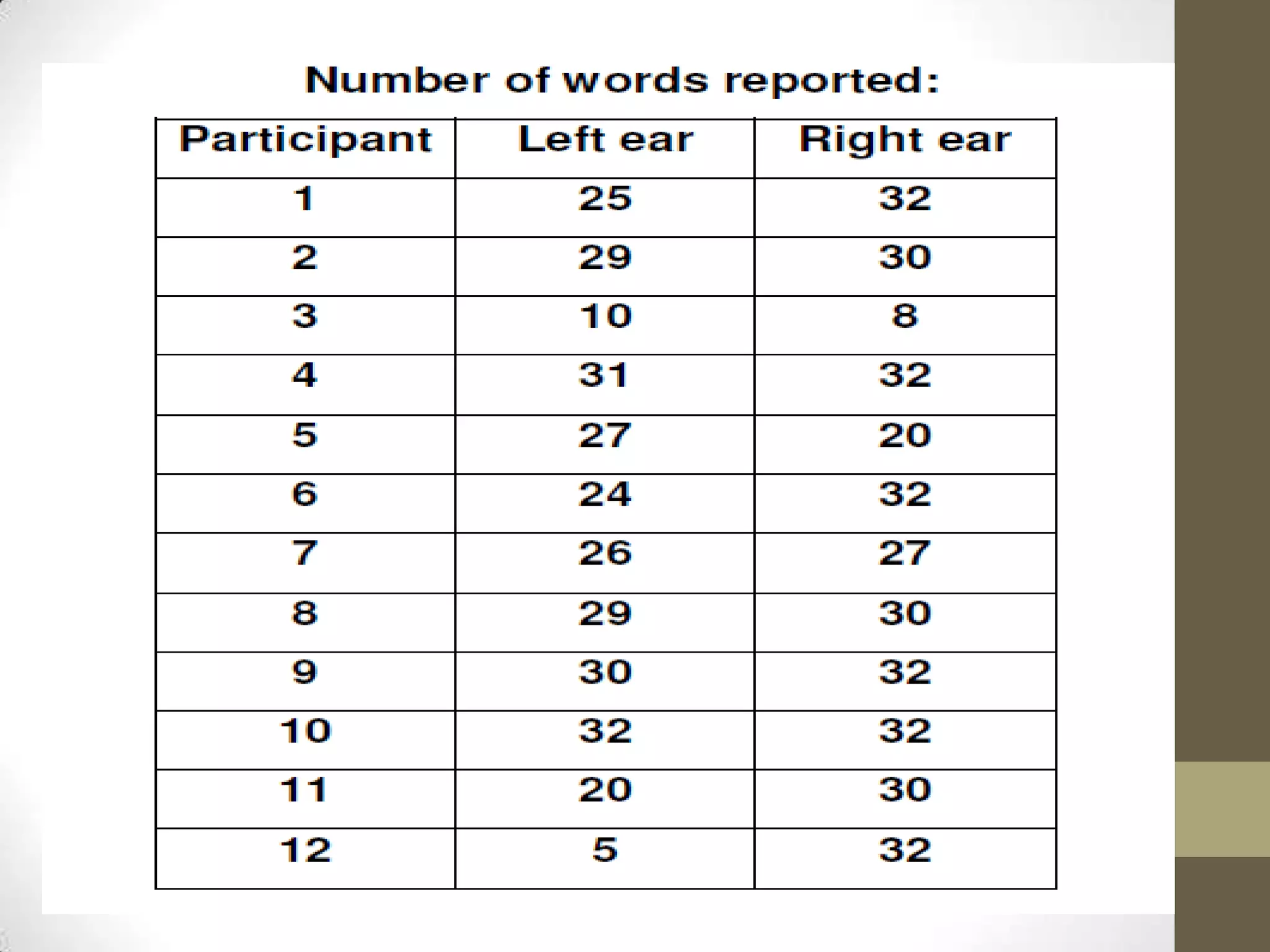
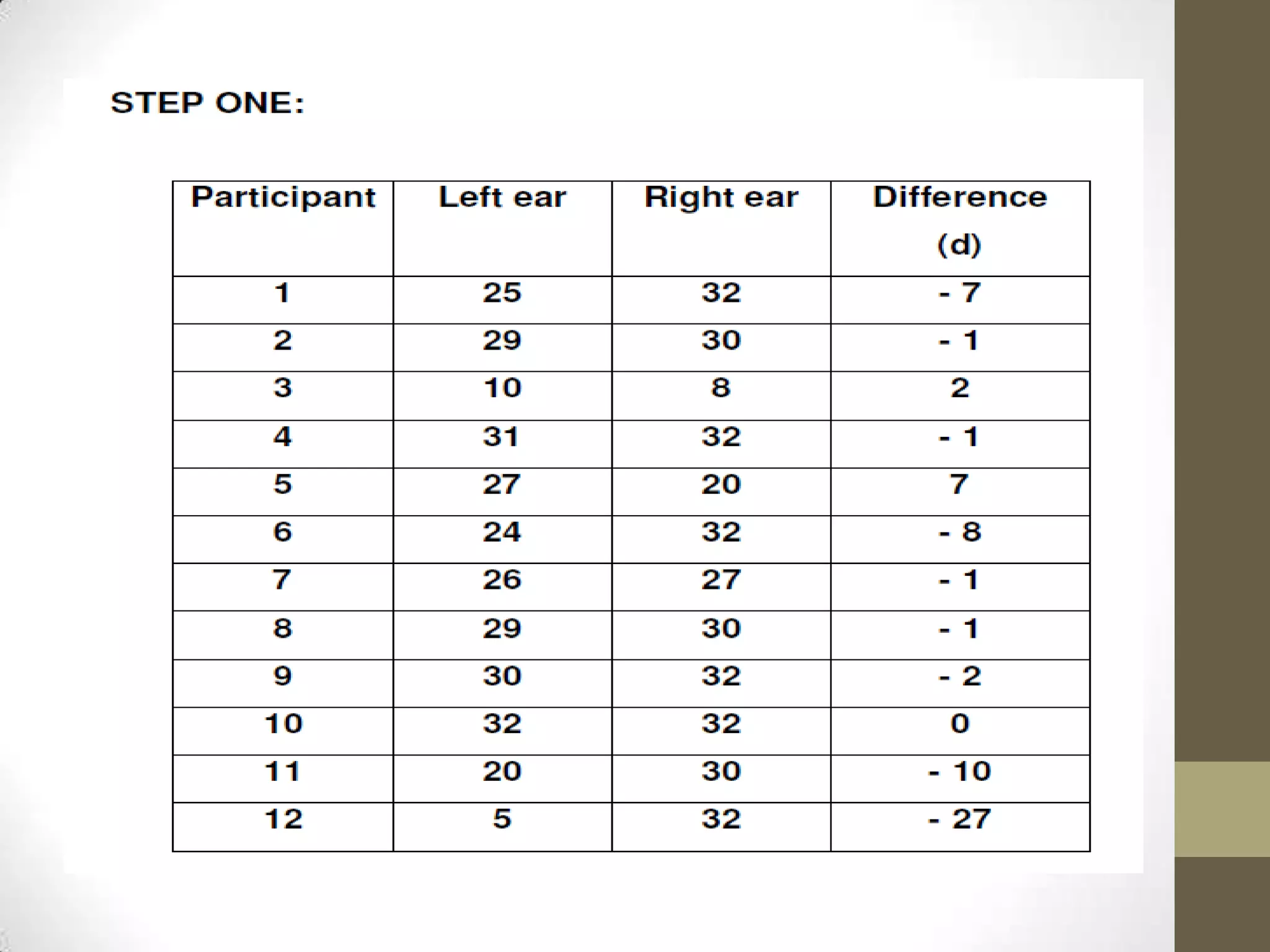
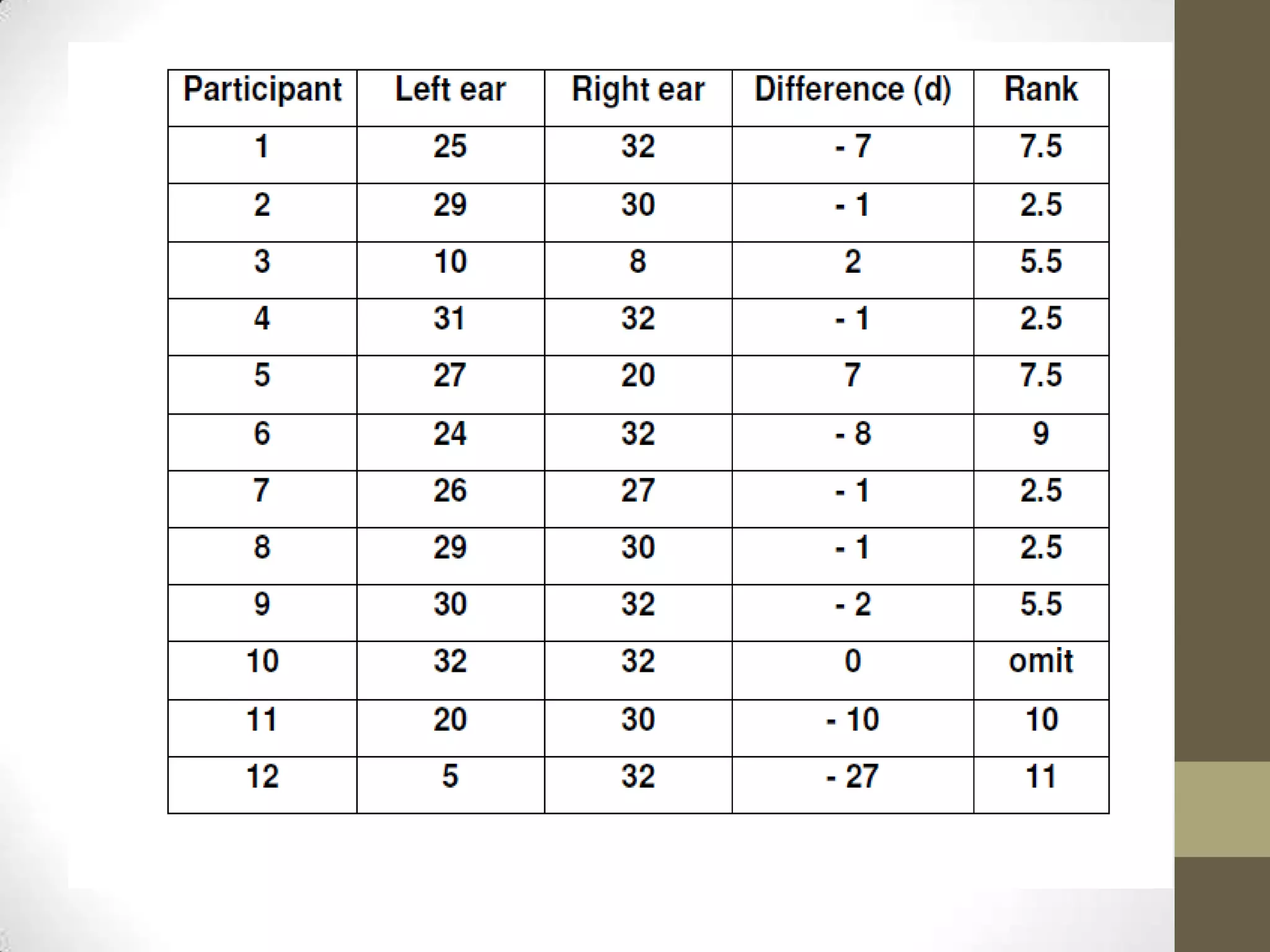
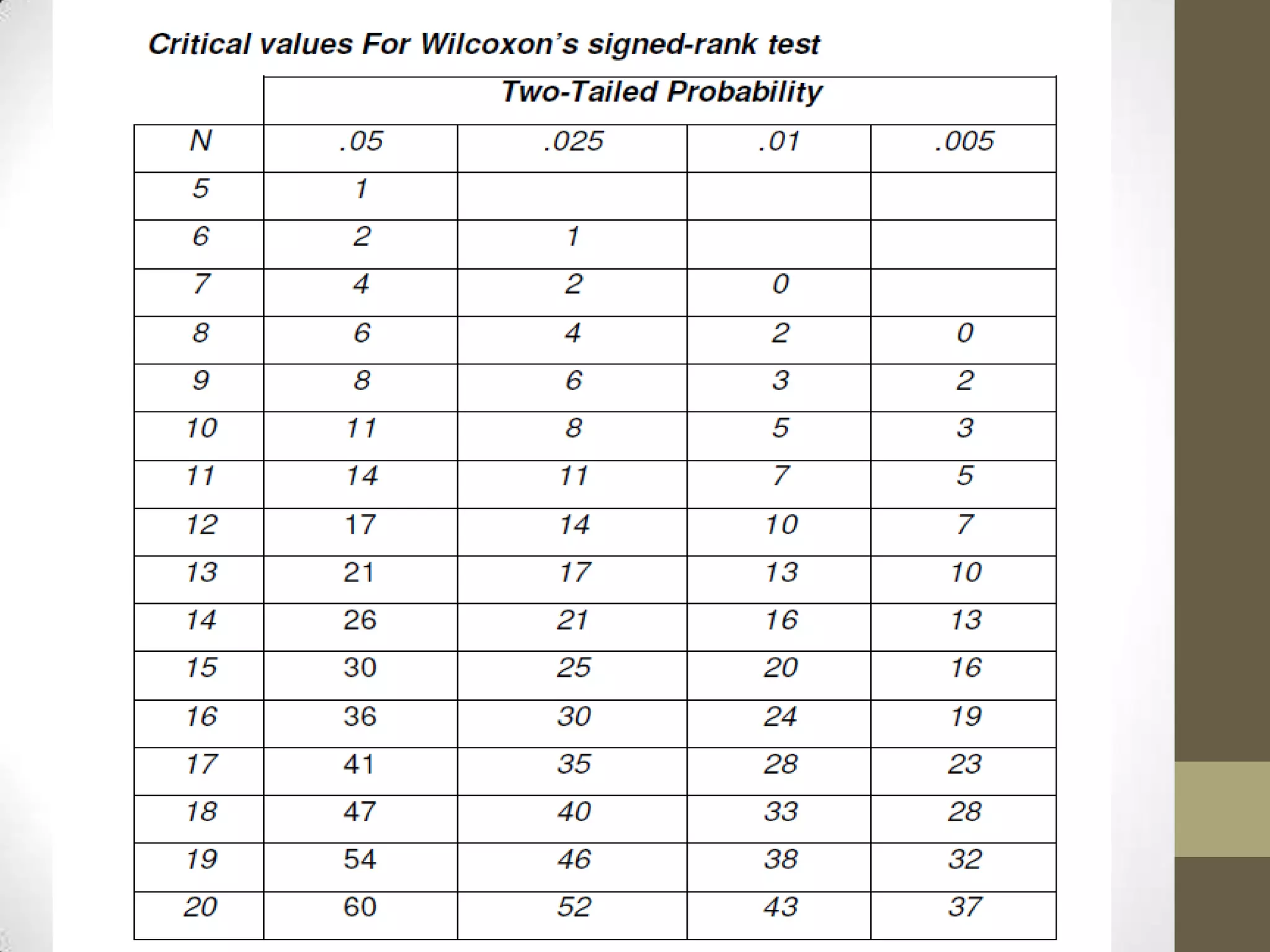
The Wilcoxon signed-rank test is a non-parametric test used to compare two related samples, such as repeated measurements on a single sample, to assess whether their population mean ranks differ. It can be used as a non-parametric alternative to the paired Student's t-test when the population cannot be assumed to be normally distributed. The test involves ranking the differences between pairs of observations and comparing the sum of the ranks of the positive differences to what would be expected if there was no effect. The document provides information on the requirements, formula, and an example application of the Wilcoxon signed-rank test.

1. Wilcoxon signedrank test
Advance Statistics
Joshua Batalla
MP-Industrial

2. Introduction of the statistical
concept
• The test is named for Frank Wilcoxon (1892–1965)
• The Wilcoxon Signed Ranks test is designed to test a
hypothesis about the location (median) of a population
distribution. It often involves the use of matched pairs, for
example, before and after data, in which case it tests for a
median difference of zero.
• The Wilcoxon Signed Ranks test does not require the
assumption that the population is normally distributed

3. Uses of Wilcoxon signed rank test
• You use the Wilcoxon signed-rank test when there are
two nominal variables and onemeasurement variable. One of
the nominal variables has only two values, such as "before"
and "after," and the other nominal variable often represents
individuals. This is the non-parametric analogue to the paired
t-test, and should be used if the distribution of differences
between pairs may be non-normally distributed.

4. Requirements
• Data are paired and come from the same population.
• Each pair is chosen randomly and independent.
• The data are measured at least on an ordinal scale, but need
not be normal.
• The distribution of the differences is symmetric around the
median

5. Formula
Let
let
be the sample size, the number of pairs. Thus, there are a total of 2N data points. For
and
,
denote the measurements.
H0: median difference between the pairs is zero
H1: median difference is not zero.
1. For
, calculate
and
, where
is
the sign function.
2. Exclude pairs with
3. Order the remaining
difference,
. Let
be the reduced sample size.
pairs from smallest absolute difference to largest absolute
.
4. Rank the pairs, starting with the smallest as 1. Ties receive a rank equal to the average of
the ranks they span. Let
Calculate the test statistic
denote the rank.

6. Formula
, the absolute value of the sum of the signed ranks.
1.
As
For
increases, the sampling distribution of
converges to a normal distribution. Thus,
, a z-score can be calculated
as
.
If
then reject
For
,
If
is compared to a critical value from a reference table.[1]
then reject
Alternatively, a p-value can be calculated from enumeration of all possible combinations
of
given
.

7. Sample Application
Wilcoxon test Worked Example:
In order to investigate whether adults report verbally
presented material more accurately from their right than from
their left ear, a dichotic listening task was carried out. The data
were found to be positively skewed.