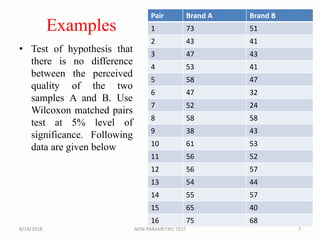
The Wilcoxon signed-rank test is a non-parametric statistical hypothesis test used to compare two related samples or repeated measurements to determine if their population mean ranks differ, serving as an alternative to the paired t-test when normal distribution cannot be assumed. It requires paired data from the same population and assesses the significance of differences in ranks. The document also includes guidelines for conducting the test and examples illustrating its application.

1. 1
Wilcoxon Signed-Rank Test
Biswash Sapkota
M. Pharma II year , Dept. of Pharmacology
SACCP, BG Nagara
8/14/2018 NON-PARAMETRIC TEST

2. Background
Parametric test Non –parametric test
It is use when the information about the
population parameters is completely
known .
It is use when there is no or few
information available about the
population parameters
It assumes that the data is normally
distributed.
It makes no assumptions about the
distribution of data.
Interval scale or ratio scale Nominal and ordinal scales
It uses mean It uses median
More powerful than non parametric Less powerful
Eg Independent sample T test, paired
sample T test, one way ANOVA can be
use.
Eg Mann-whitney test, Wilcoxon
signed rank test, Kruskal-wallis test
can be used.
8/14/2018 2NON-PARAMETRIC TEST

3. Introduction
• The Wilcoxon signed-rank test is a non-parametric
statistical hypothesis test used to compare two related
samples, matched samples, or repeated measurements on a
single sample to assess whether their population mean ranks
differ (i.e. it is a paired difference test).
• It can be used as an alternative to the paired Student's t-
test, t-test for matched pairs, or the t-test for dependent
samples when the population cannot be assumed to
be normally distributed.
8/14/2018 3NON-PARAMETRIC TEST

4. Assumptions
• Data are paired and come from the same population.
• Each paired is chosen randomly and independently.
• The data are measured on at least an interval scale when, as
is usual, within pair differences are calculated to perform
the test .
8/14/2018 4NON-PARAMETRIC TEST

5. Carrying out Wilcoxon Signed Rank
Test
Case 1:Paired data
• State the null hypothesis - in this case it is that the median
difference, M, is equal to zero.
• Calculate each paired difference, di = xi − yi, where xi, yi
are the pairs of observations.
• Rank the dis, ignoring the signs (i.e. assign rank 1 to the
smallest |di|, rank 2 to the next etc.)
• Label each rank with its sign, according to the sign of di.
• Calculate W+, the sum of the ranks of the positive dis, and
W−, the sum of the ranks of the negative dis. (As a check
the total, W+ + W−, should be equal to n(n+1)/ 2 , where n
is the number of pairs of observations in the sample).
8/14/2018 5NON-PARAMETRIC TEST

6. • Case 2: Dealing with ties
 There are two types of tied observations that may arise
when using the Wilcoxon signed rank test:
1. Observations in the sample may be exactly equal to M
(i.e. 0 in the case of paired differences). Ignore such
observations and adjust n accordingly.
2. Two or more observations/differences may be equal. If
so, average the ranks across the tied observations .If
rank 10 and 11 have the same difference than its rank
will be the average 10.5.
8/14/2018 6NON-PARAMETRIC TEST

7. Examples
• Test of hypothesis that
there is no difference
between the perceived
quality of the two
samples A and B. Use
Wilcoxon matched pairs
test at 5% level of
significance. Following
data are given below
8/14/2018 7
Pair Brand A Brand B
1 73 51
2 43 41
3 47 43
4 53 41
5 58 47
6 47 32
7 52 24
8 58 58
9 38 43
10 61 53
11 56 52
12 56 57
13 54 44
14 55 57
15 65 40
16 75 68
NON-PARAMETRIC TEST

8. Answer
• H0 : There is no difference between the perceived
quality of the two samples.
• H1 : There is difference between the perceived quality
of the two samples.
8/14/2018 8NON-PARAMETRIC TEST

9. 8/14/2018 9
Pairs Brand A Brand B Diff=A-B Abs Diff Rank Rank with tied Signs of rank
1 73 51 22 22 13 13 13
2 43 41 2 2 2 2.5 2.5
3 47 43 4 4 4 4.5 4.5
4 53 41 12 12 11 11 11
5 58 47 11 11 10 10 10
6 47 32 15 15 12 12 12
7 52 24 28 28 15 15 15
8 58 58 0 0 - - -
9 38 43 -5 5 6 6 -6
10 61 53 8 8 8 8 8
11 56 52 4 4 5 4.5 4.5
12 56 57 -1 1 1 1 -1
13 34 44 -10 10 9 9 -9
14 55 57 -2 2 3 2.5 -2.5
15 65 40 25 25 14 14 14
16 75 68 7 7 7 7 7
Total +101.5 -19.5
2 2.5
2 2.5
4
4
4.5
4.5
NON-PARAMETRIC TEST

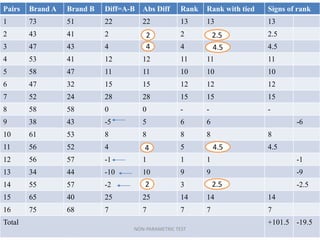
10.  Since in pair number 8 there is no significant difference
between A and B brand so total sample number is
reduced to 15.
 Total W-= [-19.5]= 19.5
 Total W+= [+101.5]= 101.5
 Since calculated value 19.5 is less than tabled value
(25) of W at 5% level of significance. Hence, we reject
the null hypothesis and concluded that there is
difference between the perceived quality of the two
samples.
8/14/2018 10NON-PARAMETRIC TEST

11. 8/14/2018 11NON-PARAMETRIC TEST