Download as PDF, PPTX
![What’s next?
LDA uses local density ρ from homogenous
electron gas
Next step: Let’s add a gradient of the density!
Generalized gradient approximation (GGA)
NANO266
2
Exc
GGA
[ρ↑
,ρ↓
]= drρ(r)εxc (∫ ρ↑
,ρ↓
, ∇ρ↑
, ∇ρ↓
)](https://image.slidesharecdn.com/05-exchange-correlationfunctionals-150406231700-conversion-gate01/85/NANO266-Lecture-5-Exchange-Correlation-Functionals-2-320.jpg)
![Why stop at the first derivative?
Meta-GGA
Example: TPSS functional
NANO266
5
Exc
meta−GGA
[ρ↑
,ρ↓
]= drρ(r)εxc (∫ ρ↑
,ρ↓
, ∇ρ↑
, ∇ρ↓
,∇2
ρ↑
,∇2
ρ↓
)
Tao, J.; Perdew, J. P.; Staroverov, V. N.; Scuseria, G. E. Climbing the density functional ladder: nonempirical meta-generalized gradient
approximation designed for molecules and solids., Phys. Rev. Lett., 2003, 91, 146401, doi:10.1103/PhysRevLett.91.146401.](https://image.slidesharecdn.com/05-exchange-correlationfunctionals-150406231700-conversion-gate01/85/NANO266-Lecture-5-Exchange-Correlation-Functionals-5-320.jpg)
Uploaded byUniversity of California, San Diego
NANO266 - Lecture 5 - Exchange-Correlation Functionals
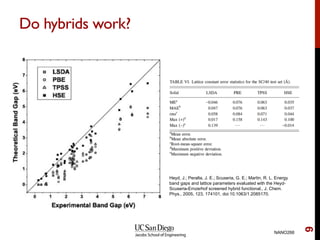
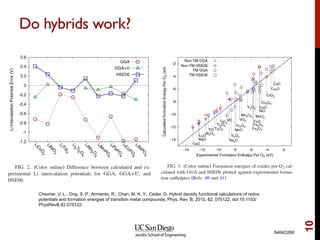
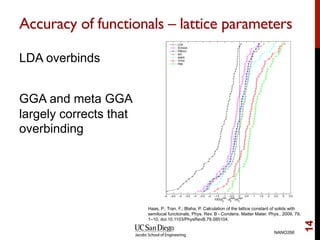
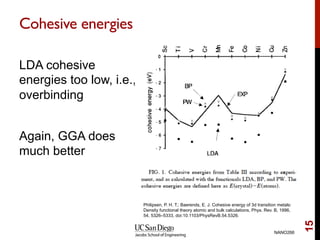
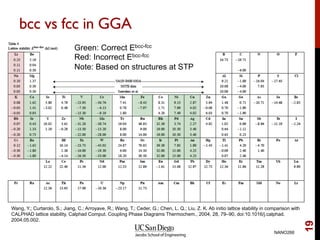
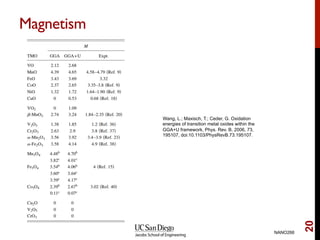
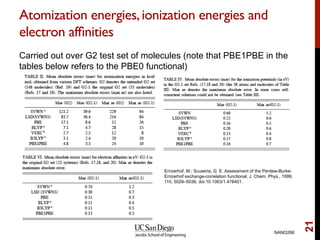
The document discusses advancements in exchange-correlation functionals used in Density Functional Theory (DFT), emphasizing the progression from Local Density Approximation (LDA) to Generalized Gradient Approximations (GGA) and meta-GGA functionals. It highlights specific functionals like BLYP, PBE, hybrid functionals like B3LYP, and their applications in improving accuracy for various properties like bond lengths, cohesive energies, and atomic structures. Additionally, it addresses the shortcomings of semi-local DFT, the need for hybrid functionals, and the accuracy trade-offs involved in DFT calculations.
More Related Content
Similar to NANO266 - Lecture 5 - Exchange-Correlation Functionals
NANO266 - Lecture 5 - Exchange-Correlation Functionals
- 1.
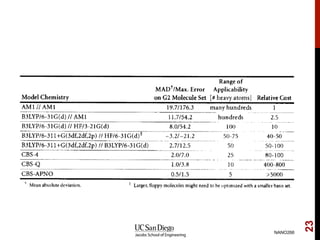
- 2. What’s next? LDA useslocal density ρ from homogenous electron gas Next step: Let’s add a gradient of the density! Generalized gradient approximation (GGA) NANO266 2 Exc GGA [ρ↑ ,ρ↓ ]= drρ(r)εxc (∫ ρ↑ ,ρ↓ , ∇ρ↑ , ∇ρ↓ )
- 3. Unlike the Highlander,thereis more than“one” GGA • BLYP, 1988: Exchange by Axel Becke based on energy density of atoms, one parameter + Correlation by Lee-Yang-Parr • PW91, 1991: Perdew-Wang 91Parametrization of real-space cut-off procedure • PBE, 1996: Perdew-Burke-Ernzerhof (re- parametrization and simplification of PW91) • RPBE, 1999: revised PBE, improves surface energetics • PBEsol, 2008: Revised PBE for solids NANO266 3
- 4. Performance of GGA GGAtends to correct LDA overbinding • Better bond lengths, lattice parameters, atomization energies, etc. NANO266 4
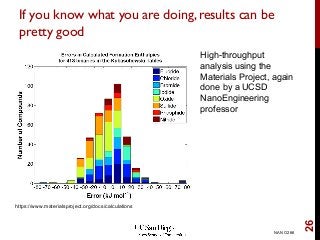
- 5. Why stop atthe first derivative? Meta-GGA Example: TPSS functional NANO266 5 Exc meta−GGA [ρ↑ ,ρ↓ ]= drρ(r)εxc (∫ ρ↑ ,ρ↓ , ∇ρ↑ , ∇ρ↓ ,∇2 ρ↑ ,∇2 ρ↓ ) Tao, J.; Perdew, J. P.; Staroverov, V. N.; Scuseria, G. E. Climbing the density functional ladder: nonempirical meta-generalized gradient approximation designed for molecules and solids., Phys. Rev. Lett., 2003, 91, 146401, doi:10.1103/PhysRevLett.91.146401.
- 6. Orbital-dependent methods DFT+U1,2,3 • Treatstrong on-site Coulomb interaction of localized electrons, e.g., d and f electrons (incorrectly described by LDA or GGA) with an additional Hubbard-like term. • Strength of on-site interactions usually described by U (on site Coulomb) and J (on site exchange), which can be extracted from ab-initio calculations,4 but usually are obtained semi-empirically, e.g., fitting to experimental formation energies or band gaps. NANO266 6 (1) Anisimov, V. I.; Zaanen, J.; Andersen, O. K. Phys. Rev. B, 1991, 44, 943–954. (2) Anisimov, V. I.; Solovyev, I. V; Korotin, M. A.; Czyzyk, M. T.; Sawatzky, G. A. Phys. Rev. B, 1993, 48, 16929–16934. (3) Dudarev, S. L.; Botton, G. A.; Savrasov, S. Y.; Humphreys, C. J.; Sutton, A. P., Phys. Rev. B, 1998, 57, 1505–1509. (4) Cococcioni, M.; de Gironcoli, S., Phys. Rev. B, 2005, 71, 035105, doi:10.1103/PhysRevB.71.035105. EDFT+U = EDFT + Ueff 2 ρσ m1,m1 m1 ∑ " # $$ % & ''− ρσ m1,m2 m1m2 ∑ ρσ m2,m1 " # $$ % & '' ) * + + , - . .σ ∑ Penalty term to force on-site occupancy in the direction of of idempotency, i.e. to either fully occupied or fully unoccupied levels
- 7. Where do Iget U values 1. Fit it yourself, either using linear response approach or to some experimental data that you have for your problem at hand 2. Use well-tested values in the literature, e.g., for high-throughput calculations (though you should use caution!) NANO266 7 U values used in the Materials Project, fitted by a UCSD NanoEngineering Professor
- 8. Hybrids NANO266 8 Chimera from Godof War (memories of times when I was still a carefree graduate student) HF DFT
- 9. Rationale for Hybrids Semi-localDFT suffer from the dreaded self- interaction error • Spurious interaction of the electron not completely cancelled with approximate Exc NANO266 9 Eee = 1 2 ρi (ri )ρj (rj) rij dri drj∫∫ Ex HF = − 1 2 ρi (ri )ρj (rj) rij dri drj∫∫ Includes interaction of electron with itself! HF Exchange cancels self- interaction by construction
- 10. Typical Hybrid Functionals B3LYP(Becke 3-parameter, Lee-Yang-Parr) • Arguably the most popular functional in quantum chemistry (the 8th most cited paper in all fields) • Originally fitted from a set of atomization energies, ionization potentials, proton affinities and total atomic energies. PBE0: HSE (Heyd-Scuseria-Ernzerhof) (2006): • Effectively PBE0, but with an adjustable parameter controlling the range of the exchange interaction. Hence, known as a screened hybrid functional • Works remarkably well for extended systems like solids NANO266 10 Exc B3LYP = Ex LDA + ao (Ex HF − Ex LDA )+ ax (Ex GGA − Ex LDA )+ Ec LDA +(Ec GGA − Ec LDA ) where a0 = −0.20, ax = 0.72, ac = 0.81 Exc PBE0 = 1 4 Ex HF + 3 4 Ex PBE + Ec PBE Exc HSE = aEx HF,SR (ω)+(1− a)Ex PBE,SR (ω)+ Ex PBE,LR (ω)+ Ec PBE a = 1 4 , ω = 0.2
- 11. Do hybrids work? NANO266 11 Heyd,J.; Peralta, J. E.; Scuseria, G. E.; Martin, R. L. Energy band gaps and lattice parameters evaluated with the Heyd- Scuseria-Ernzerhof screened hybrid functional., J. Chem. Phys., 2005, 123, 174101, doi:10.1063/1.2085170.
- 12. Do hybrids work? NANO266 12 Chevrier,V. L.; Ong, S. P.; Armiento, R.; Chan, M. K. Y.; Ceder, G. Hybrid density functional calculations of redox potentials and formation energies of transition metal compounds, Phys. Rev. B, 2010, 82, 075122, doi:10.1103/ PhysRevB.82.075122.
- 13.
- 14. Which functional touse? NANO266 14
- 15. To answer thatquestion,we need to go back to our trade-off trinity NANO266 15 Choose two (sometimes you only get one) Accuracy Computational Cost System size
- 16. Accuracy of functionals– lattice parameters LDA overbinds GGA and meta GGA largely corrects that overbinding NANO266 16 Haas, P.; Tran, F.; Blaha, P. Calculation of the lattice constant of solids with semilocal functionals, Phys. Rev. B - Condens. Matter Mater. Phys., 2009, 79, 1–10, doi:10.1103/PhysRevB.79.085104.
- 17. Cohesive energies LDA cohesive energiestoo low, i.e., overbinding Again, GGA does much better NANO266 17 Philipsen, P. H. T.; Baerends, E. J. Cohesive energy of 3d transition metals: Density functional theory atomic and bulk calculations, Phys. Rev. B, 1996, 54, 5326–5333, doi:10.1103/PhysRevB.54.5326.
- 18. Bond lengths NANO266 18 Cramer, C.J. Essentials of Computational Chemistry: Theories and Models; 2004.
- 19. Conclusion – LDAvs GGA LDA almost always underpredicts bond lengths, lattice parameters and overbinds GGA error is smaller, but less systematic. Error in GGA < 1% in many cases Conclusion • Very little reason to choose LDA over GGA since computational cost are similar Note: In all cases, we assume that LDA and GGA refers to spin-polarized versions. NANO266 19
- 20. Predicting structure Atomic energy:-1894.074 Ry Fcc V : -1894.7325 Ry Bcc V : -1894.7125 Ry Cohesive energy = 0.638 Ry (0.03% of total E) Fcc/bcc difference = 0.02 Ry (0.001% of total E) Mixing energies ~ 10-6 fraction of total E NANO266 20 Ref: MIT 3.320 Lectures on Atomistic Modeling of Materials
- 21. bcc vs fccin GGA NANO266 21 Green: Correct Ebcc-fcc Red: Incorrect Ebcc-fcc Note: Based on structures at STP Wang, Y.; Curtarolo, S.; Jiang, C.; Arroyave, R.; Wang, T.; Ceder, G.; Chen, L. Q.; Liu, Z. K. Ab initio lattice stability in comparison with CALPHAD lattice stability, Calphad Comput. Coupling Phase Diagrams Thermochem., 2004, 28, 79–90, doi:10.1016/j.calphad.2004.05.002.
- 22. Magnetism NANO266 22 Wang, L.; Maxisch,T.; Ceder, G. Oxidation energies of transition metal oxides within the GGA+U framework, Phys. Rev. B, 2006, 73, 195107, doi:10.1103/PhysRevB.73.195107.
- 23. Atomization energies,ionization energiesand electron affinities Carried out over G2 test set of molecules (note that PBE1PBE in the tables below refers to the PBE0 functional) NANO266 23 Ernzerhof, M.; Scuseria, G. E. Assessment of the Perdew-Burke- Ernzerhof exchange-correlation functional, J. Chem. Phys., 1999, 110, 5029–5036, doi:10.1063/1.478401.
- 24. Reaction energies Broad conclusions • GGA better than LSDA • Hybrids most efficient (good accuracy comparable to highly correlated methods) NANO266 24
- 25. Some well-known problemscan be addressed by judicious fitting to experimental data NANO266 25 Wang, L.; Maxisch, T.; Ceder, G. Oxidation energies of transition metal oxides within the GGA+U framework, Phys. Rev. B, 2006, 73, 195107, doi: 10.1103/PhysRevB.73.195107. Stevanović, V.; Lany, S.; Zhang, X.; Zunger, A. Correcting density functional theory for accurate predictions of compound enthalpies of formation: Fitted elemental-phase reference energies, Phys. Rev. B, 2012, 85, 115104, doi:10.1103/PhysRevB.85.115104.
- 26. If you knowwhat you are doing,results can be pretty good High-throughput analysis using the Materials Project, again done by a UCSD NanoEngineering professor NANO266 26 https://www.materialsproject.org/docs/calculations
- 27. Band gaps In anutshell, really bad in semi-local DFT. But we knew this going into KS DFT… Hybrids fare much better New functionals and methods have been developed to address this problem • GLLB functional1 • ΔSCF for solids2 NANO266 27 https://www.materialsproject.org/docs/calculations (1) Kuisma, M.; Ojanen, J.; Enkovaara, J.; Rantala, T. T. Phys. Rev. B, 2010, 82, doi:10.1103/PhysRevB. 82.115106. (2) Chan, M.; Ceder, G. Phys. Rev. Lett., 2010, 105, 196403, doi:10.1103/PhysRevLett.105.196403.