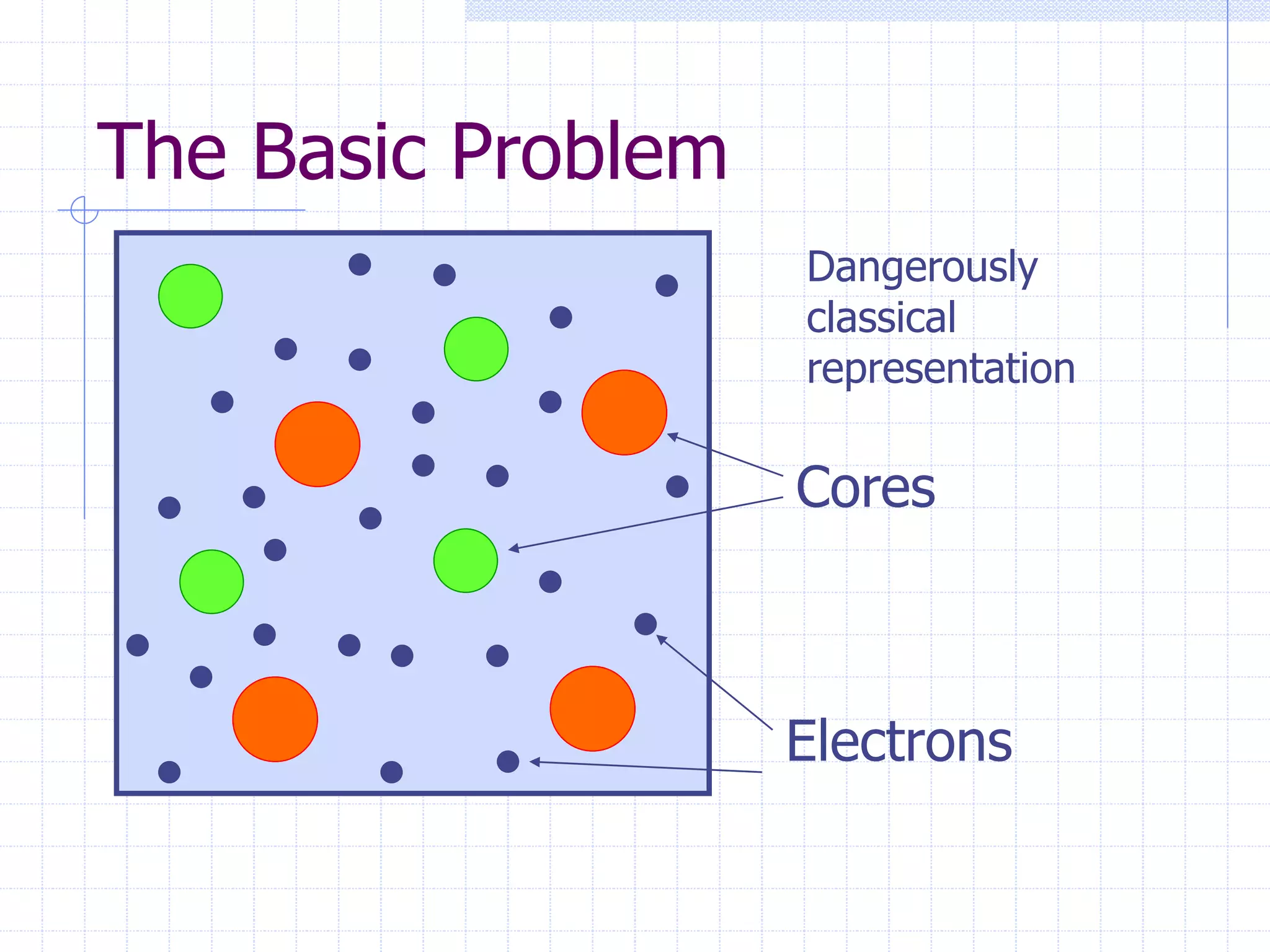
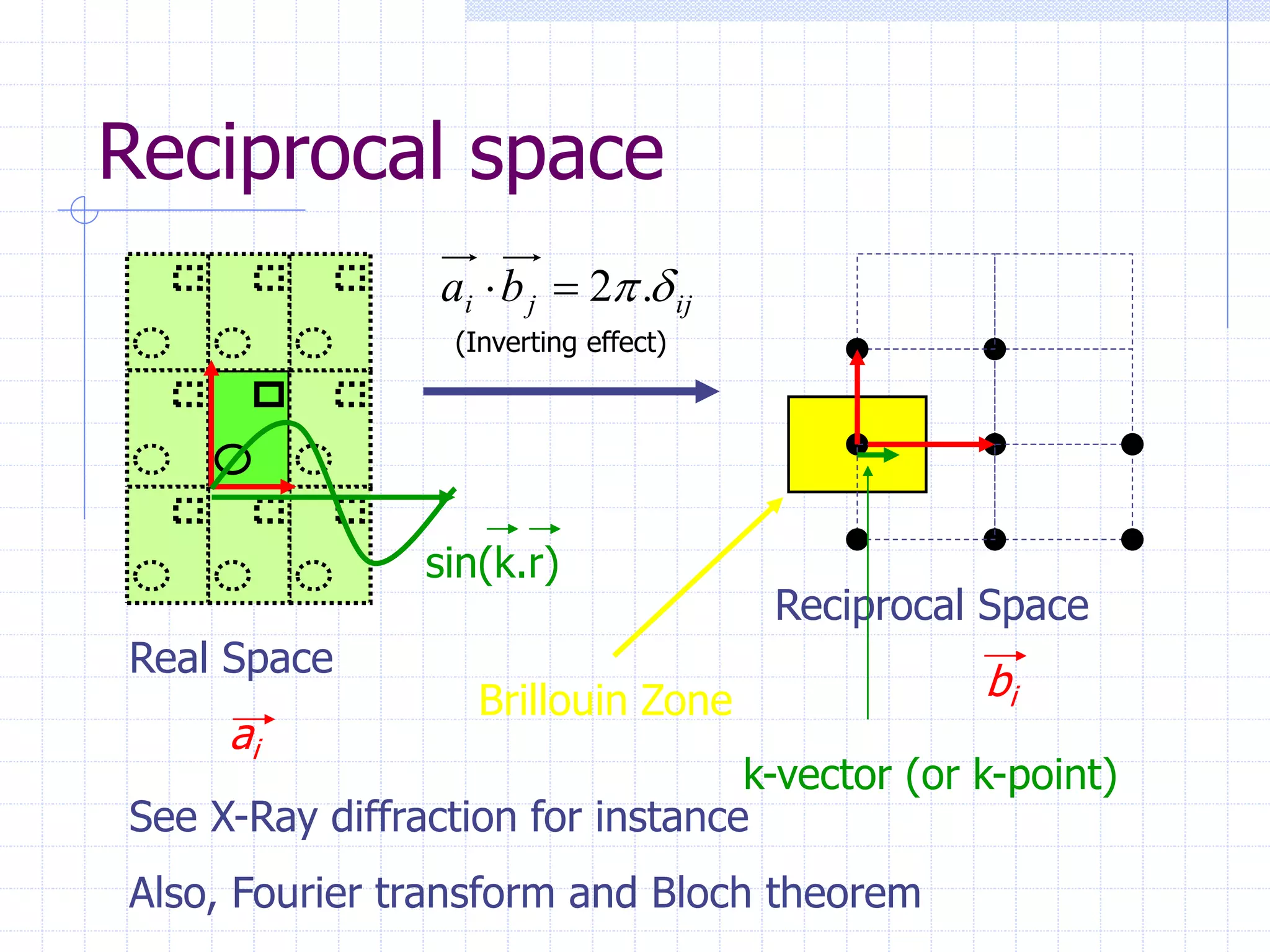
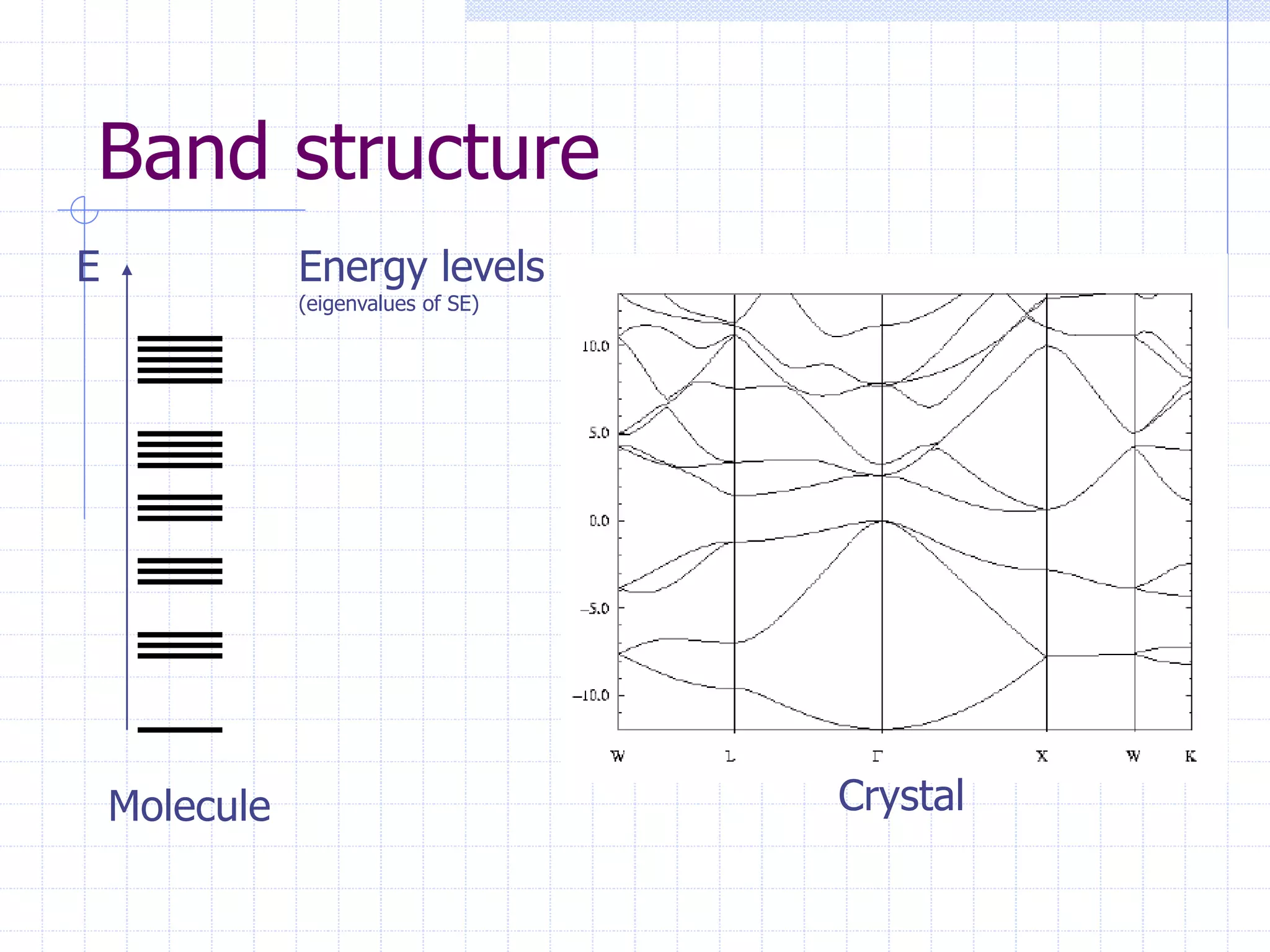
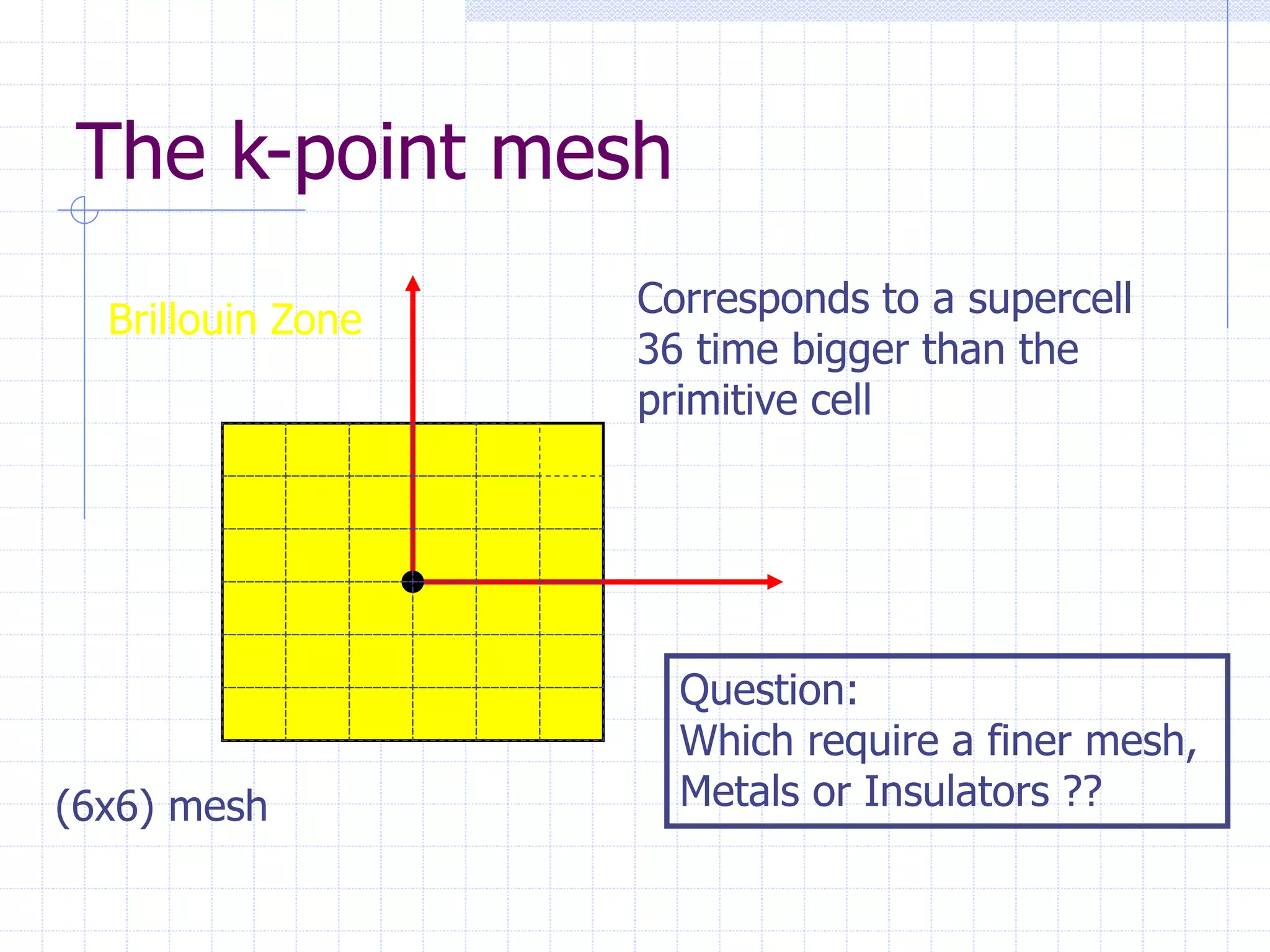
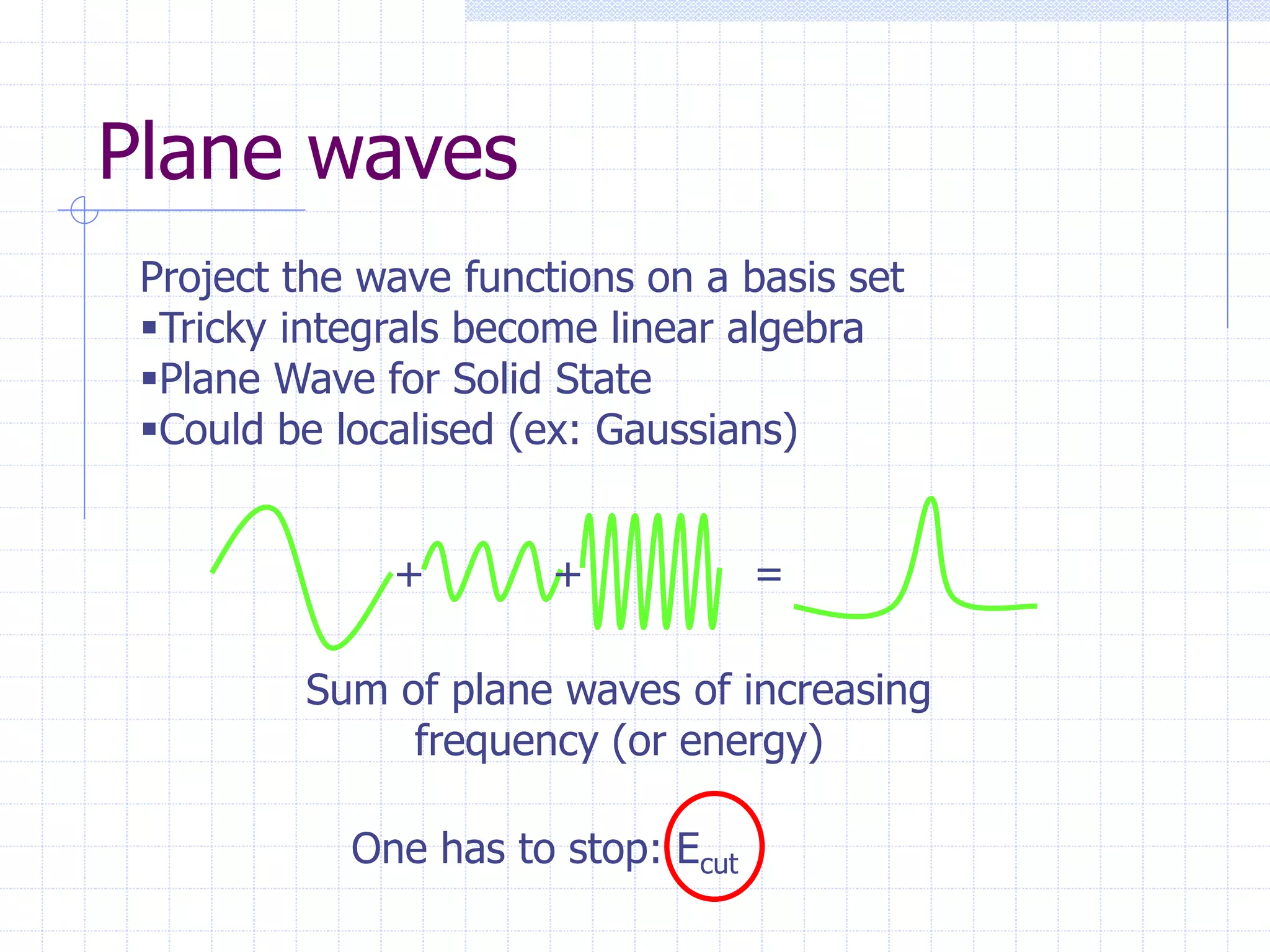
This document serves as a comprehensive introduction to density-functional theory (DFT), outlining fundamental concepts such as the Hohenberg-Kohn theorem, the Kohn-Sham equations, and practical considerations for implementing DFT in computational chemistry. It discusses the theoretical framework, simplifications for solving the Schrödinger equation, and the significance of electronic density in determining ground state energy. Additional sections cover applications in solid state physics, including band structure and energy optimization techniques.

1. Computational Chemistry:
A DFT crash course

2. Useful Material
Books
 A chemist’s guide to density-functional theory
Wolfram Koch and Max C. Holthausen (second edition,
Wiley)
 The theory of the cohesive energies of solids
G. P. Srivastava and D. Weaire
Advances in Physics 36 (1987) 463-517
 Gulliver among the atoms
Mike Gillan, New Scientist 138 (1993) 34
Web
 www.nobel.se/chemistry/laureates/1998/
 www.abinit.org
Version 4.2.3 compiled for windows, install and good
tutorial

3. Outline: Part 1,
The Framework of DFT
DFT: the theory
 Schroedinger’s equation
 Hohenberg-Kohn Theorem
 Kohn-Sham Theorem
 Simplifying Schroedinger’s
 LDA, GGA
Elements of Solid State Physics
 Reciprocal space
 Band structure
 Plane waves
And then ?
 Forces (Hellmann-Feynman theorem)
 E.O., M.D., M.C. …

4. Outline: Part2
Using DFT
Practical Issues
 Input File(s)
 Output files
 Configuration
 K-points mesh
 Pseudopotentials
 Control Parameters
 LDA/GGA
 ‘Diagonalisation’
Applications
 Isolated molecule
 Bulk
 Surface

5. The Basic Problem
Dangerously
classical
representation
Cores
Electrons

6. Schroedinger’s Equation
   
i
i
i
i r
R
r
R
V
m
,
.
,
2
2











 

Hamiltonian operator
Kinetic Energy
Potential Energy
Coulombic interaction
External Fields
Very Complex many body Problem !!
(Because everything interacts)
Wave function
Energy levels

7. First approximations
Adiabatic (or Born-Openheimer)
 Electrons are much lighter, and faster
 Decoupling in the wave function
Nuclei are treated classically
 They go in the external potential
     
i
i
i
i r
R
r
R 
 .
, 


8. H.K. Theorem
The ground state is unequivocally
defined by the electronic density
        r
r
r d
v
F
Ev 

 


Universal functional
•Functional ?? Function of a function
•No more wave functions here
•But still too complex

9. K.S. Formulation
Use an auxiliary system
 Non interacting electrons
 Same Density
 => Back to wave functions, but simpler this time
(a lot more though)
   
r
r
V
m
i
i
i
eff 

 .
2
2











        
r
r
r
r
r
r
r 


XC
eff d
V
V 





 
   


i
i
2
r
r 

N K.S. equations
(ONE particle in a box really)
(KS3)
(KS2)
(KS1)
Exchange correlation potential

10. Self consistent loop
Solve the independents K.S.
=>wave functions
From density, work out
Effective potential
New density ‘=‘
input density ??
Deduce new density from w.f.
Initial density
Finita la musica
YES
NO

11. DFT energy functional
           




 XC
NI E
d
d
d
v
T
E 






 
 r
r
r
r
r
r
r
r
2
1
Exchange correlation funtional
Contains:
Exchange
Correlation
Interacting part of K.E.
Electrons are fermions
(antisymmetric wave function)

12. Exchange correlation functional
At this stage, the only thing we need is:  

XC
E
Still a functional (way too many variables)
#1 approximation, Local Density Approximation:
Homogeneous electron gas
Functional becomes function !! (see KS3)
Very good parameterisation for  

XC
E
Generalised Gradient Approximation:
 

 
,
XC
E
GGA
LDA

13. DFT: Summary
The ground state energy depends only on
the electronic density (H.K.)
One can formally replace the SE for the
system by a set of SE for non-interacting
electrons (K.S.)
Everything hard is dumped into Exc
Simplistic approximations of Exc work !
LDA or GGA

14. And now, for something completely different:
A little bit of Solid State Physics
Crystal structure Periodicity

15. Reciprocal space
Real Space
ai
ij
j
i b
a 
.
2


Reciprocal Space
bi
Brillouin Zone
(Inverting effect)
k-vector (or k-point)
sin(k.r)
See X-Ray diffraction for instance
Also, Fourier transform and Bloch theorem

16. Band structure
Molecule
E
Crystal
Energy levels
(eigenvalues of SE)

17. The k-point mesh
Brillouin Zone
(6x6) mesh
Corresponds to a supercell
36 time bigger than the
primitive cell
Question:
Which require a finer mesh,
Metals or Insulators ??

18. Plane waves
Project the wave functions on a basis set
Tricky integrals become linear algebra
Plane Wave for Solid State
Could be localised (ex: Gaussians)
+ + =
Sum of plane waves of increasing
frequency (or energy)
One has to stop: Ecut

19. Solid State: Summary
Quantities can be calculated in the
direct or reciprocal space
k-point Mesh
Plane wave basis set, Ecut

20. Now what ?
We have access to the energy of a system,
without any empirical input
With little efforts, the forces can be computed,
Hellman-Feynman theorem
Then, the methodologies discussed for atomistic potential
can be used
Energy Optimisation
Monte Carlo
Molecular dynamics
   
 



 r
r
r
F d
v i
i
i 