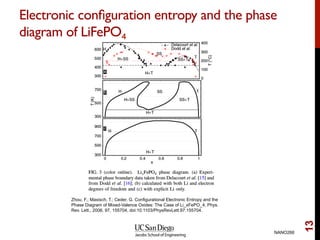
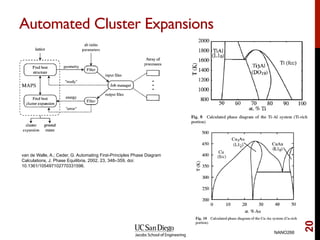
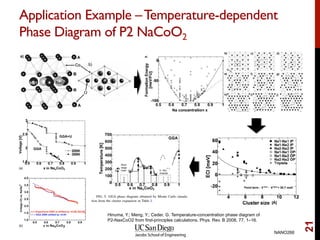
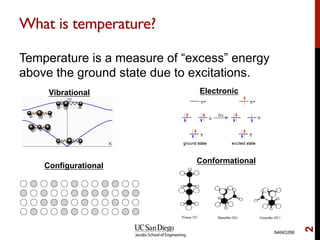
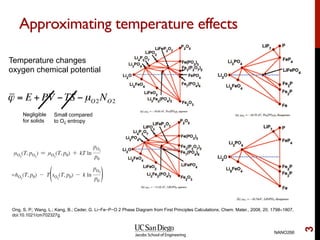
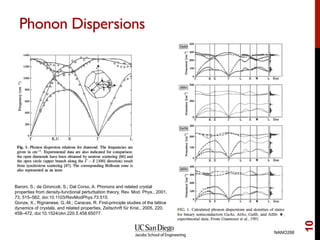
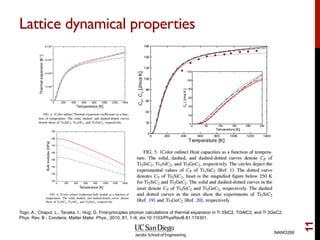
The document discusses the concept of temperature as a measure of energy above the ground state due to excitations, highlighting its effects on vibrational, configurational, and electronic properties in materials. Various methods for calculating acoustic properties such as phonons through density functional theory (DFT) and other approaches are examined, each with its advantages and disadvantages. It also touches on topics such as electronic entropy, phase diagrams, and methodologies for automating first-principles calculations for materials science.

1. ModelingTemperature
Shyue Ping Ong

2. What is temperature?
Temperature is a measure of “excess” energy
above the ground state due to excitations.
NANO266
2
Vibrational
Configurational
Electronic
Conformational

3. Approximating temperature effects
NANO266
3
ϕ = E + PV −TS −µO2 NO2
Negligible
for solids
Small compared
to O2 entropy
Ong, S. P.; Wang, L.; Kang, B.; Ceder, G. Li−Fe−P−O 2 Phase Diagram from First Principles Calculations, Chem. Mater., 2008, 20, 1798–1807,
doi:10.1021/cm702327g.
Temperature changes
oxygen chemical potential

4. Vibrational entropy - Phonons
Collective excitation in a periodic, elastic
arrangement of atoms or molecules in condensed
matter, like solids and some liquids.
NANO266
4

5. Lattice dynamics of monoatomic 1D lattice
NANO266
5
(n-2)a (n-1)a na (n+1)a (n+2)a
un un+1 un+2un-1un-2
E0 ({un}) = E0 (0)+
∂E
∂un
"
#
$
%
&
'
0
un
n
∑ +
1
2
∂2
E
∂un∂un
)
"
#
$
$
%
&
'
'
0
unun
)
n, )n
∑ +
1
3!
∂3
E
∂un∂un
)∂un
))
"
#
$
$
%
&
'
'
0
ununun
))
n, )n , ))n
∑ +…
At equilibrium
E0 ({un}) ≈ E0 (0)+
1
2
Dn, "n unun
"
n, "n
∑ where Dn, "n =
∂2
E
∂un∂un
"
%
&
'
'
(
)
*
*
0
Harmonic approximation
M!!un = − Dn, "n un
"
"n
∑
un = Aei(qna−ωt)
Classical picture

6. DirectApproach –“Frozen” phonons
Explicitly calculate the forces between every atom and construct the
force constant matrix of the crystal, and hence calculate normal
modes of at any particular wavevector, q.
Forces can be obtained in DFT using Hellman-Feynman Theorem
Pros:
• No specialized code required (except for automating displacements, etc.)
• Faster than linear response method, especially for reasonably sized systems.
• Many existing codes to help automate such computations: Phonopy, GoBaby, etc.
• Higher order anharmonic terms can be obtained relatively easily
Cons:
• Large supercells are needed to accurately calculate the force constant matrix.
NANO266
6
∂E
∂λ
= ψλ
* ∂H
∂λ
ψλ dV∫

7. Linear Response Method – Density Functional
PerturbationTheory
From the Hellman-Feynman Theorem, we have
Linearizing the electron density, we get
NANO266
7
∂E
∂λi
=
∂Vλ (r)
∂λi
nλ (r)dr∫
∂2
E
∂λi∂λj
=
∂2
Vλ (r)
∂λi∂λj
nλ
(r)dr +∫
∂Vλ (r)
∂λi
∂nλ
(r)
∂λj
dr∫
Δn(r) = 4Re ψ*
n (r)Δψn (r)
n=1
N/2
∑
Baroni, S.; de Gironcoli, S.; Dal Corso, A. Phonons and related crystal properties from density-functional perturbation theory, Rev. Mod.
Phys., 2001, 73, 515–562, doi:10.1103/RevModPhys.73.515.

8. Linear Response Method – Density Functional
PerturbationTheory
From first order perturbation theory, we have
where
NANO266
8
(HSCF −εn ) Δψn = −(ΔVSCF − Δεn ) Δψn
ΔVSCF (r) = ΔV(r)+e2 Δn( "r )
r − "r
d "r∫ +
dvxc
dn n=n(r)
Δn(r)
Baroni, S.; de Gironcoli, S.; Dal Corso, A. Phonons and related crystal properties from density-functional perturbation theory, Rev. Mod.
Phys., 2001, 73, 515–562, doi:10.1103/RevModPhys.73.515.

9. DFPT
Pros:
• Can calculate phonon frequencies at arbitrary wave vectors q
without use of supercells!
• Scaling with range of interatomic force constants is much more
favorable.
Cons:
• Requires specialized codes
• Cost of calculations typically higher than frozen phonons
approach.
NANO266
9

10. Phonon Dispersions
NANO266
10
Baroni, S.; de Gironcoli, S.; Dal Corso, A. Phonons and related crystal
properties from density-functional perturbation theory, Rev. Mod. Phys., 2001,
73, 515–562, doi:10.1103/RevModPhys.73.515.
Gonze, X.; Rignanese, G.-M.; Caracas, R. First-principle studies of the lattice
dynamics of crystals, and related properties, Zeitschrift für Krist., 2005, 220,
458–472, doi:10.1524/zkri.220.5.458.65077.

11. Lattice dynamical properties
NANO266
11
Togo, A.; Chaput, L.; Tanaka, I.; Hug, G. First-principles phonon calculations of thermal expansion in Ti 3SiC2, Ti3AlC2, and Ti 3GeC2,
Phys. Rev. B - Condens. Matter Mater. Phys., 2010, 81, 1–6, doi:10.1103/PhysRevB.81.174301.

12. Electronic entropy
Probablity is given by Fermi-Dirac function
NANO266
12
hi
KS
= −
1
2
∇2
−
Zk
rik
+
k
∑
1
2
ρ(r')
ri − r'
dr∫∫ '+Vxc[ρ(r)]
hi
KS
ψi (r) =εiψi (r) Independent one-electron eigenstates can
be occupied or not
fi =
e−β(εi−εF )
1+e−β(εi−εF )
Sel = −kB fi ln( fi )+(1− fi )ln(1− fi )[ ]
i
∑

13. Electronic configuration entropy and the phase
diagram of LiFePO4
NANO266
13
Zhou, F.; Maxisch, T.; Ceder, G. Configurational Electronic Entropy and the
Phase Diagram of Mixed-Valence Oxides: The Case of Li_xFePO_4, Phys.
Rev. Lett., 2006, 97, 155704, doi:10.1103/PhysRevLett.97.155704.

14. Configuration Entropy – Ising Model
If J >0 -> Ferromagnetic ground state
If J<0 -> Anti-ferromagnetic ground state
In absence of magnetic field, system is
permanently magnetized at low
temperatures.
At Curie temperature, Tc, phase
transition occurs between magnetic and
paramagnetic phases (magnetization is
zero).
NANO266
14
H(σ ) = − Jijσiσ j
<ij>
∑ −µ hjσ j
j
∑

15. Cluster expansion formalism
Generalization of Ising model
Partition function
NANO266
15
E σ( )=V0
+ Vi
σi
i
∑ + Vij
σi
σ j
i, j
∑ + Vijk
σi
σ j
i, j,k
∑ σk
+…
Z = E σ( )
σ
∑

16. Thermodynamic averages from Monte Carlo
simulations
Sample states of a system stochastically with probabilities
that match those expected physically
To perform the integral numerically,
NANO266
16
A = Aσ
e−βE(σ )
Zσ
∫ dσ
A = Aσ
e−βE(σ )
Zσ
∑ = Aσ p(σ )
σ
∑

17. Simple sampling (random choice of states) is inefficient
because thermodynamic probabilities are very sharply
peaked (exponential term)!
Simple sampling
NANO266
17
p(σ)
States here contributes
≈0 to integral
Nearly all the contributions
to integral comes from here
Is there a better sampling
method?

18. Detailed balance
At steady state, flux between two states must be equal, i.e.,
If the attempt distributions are symmetric, i.e., random selection,
So we set
NANO266
18
p(m)π(m → n) = p(n)π(n → m)
where π(m → n) = a(m → n)A(m → n)
π is the transition matrix and is given by the product of the attempt distribution a
and the acceptance distribution A.
a(m → n) = a(n → m)
p(m)A(m → n) = p(n)A(n → m)
A(m → n)
A(n → m)
=
p(n)
p(m)
= e−β(En−Em )
A(m → n) =
e−β(En−Em )
if p(n) < p(m)
1 if p(n) > p(m)
#
$
%
&%

19. Metropolis algorithm for cluster expansions
1. Start in state {σ1, σ2, …, σn}.
2. Choose a new set of spins by “flipping” randomly selected σi* = -
σi
3. Calculate ΔE = E({σ1,…, -σi, …, σn}) - E({σ1,…, σi, …, σn})
4. If ΔE < 0, accept σi*. If ΔE > 0, accept σi* with probability e-βΔE.
5. Go back to step 1.
NANO266
19
Example: Modeling a atomic
orderings in an alloy

20. Automated Cluster Expansions
NANO266
20
van de Walle, A.; Ceder, G. Automating First-Principles Phase Diagram
Calculations, J. Phase Equilibria, 2002, 23, 348–359, doi:
10.1361/105497102770331596.

21. Application Example –Temperature-dependent
Phase Diagram of P2 NaCoO2
NANO266
21
Hinuma, Y.; Meng, Y.; Ceder, G. Temperature-concentration phase diagram of
P2-NaxCoO2 from first-principles calculations. Phys. Rev. B 2008, 77, 1–16.

22. State of the art in Cluster Expansions
NANO266
22
Van de Walle, A. A complete representation of structure-property
relationships in crystals., Nat. Mater., 2008, 7, 455–8, doi:10.1038/
nmat2200.
Compressive sensing paradigm for
determining ECIs
Configurational dependence of
property tensors
Nelson, L. J.; Hart, G. L. W.; Zhou, F.; Ozoliņš, V. Compressive
sensing as a paradigm for building physics models, Phys. Rev. B,
2013, 87, 035125, doi:10.1103/PhysRevB.87.035125.