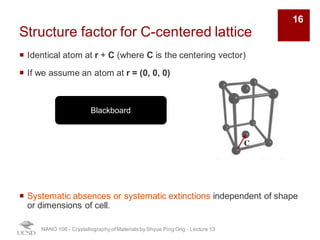
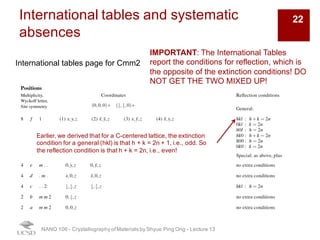
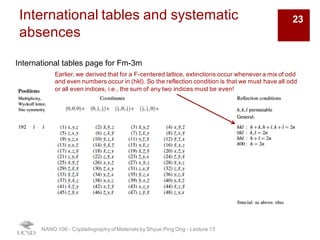
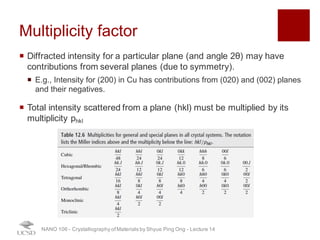
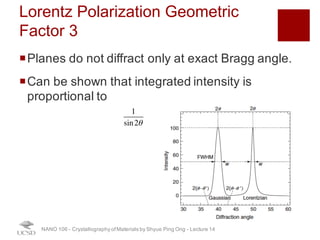
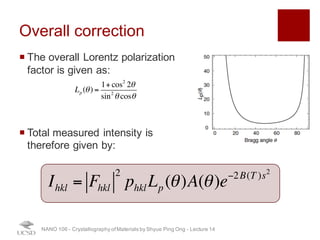
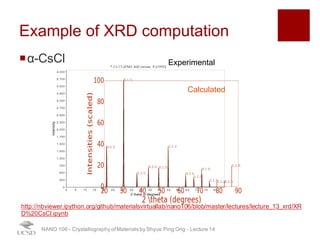
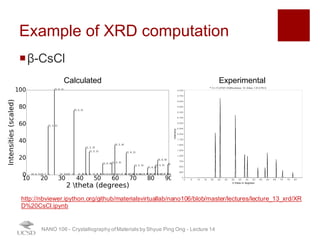
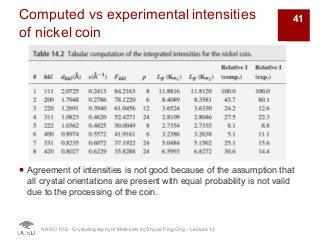
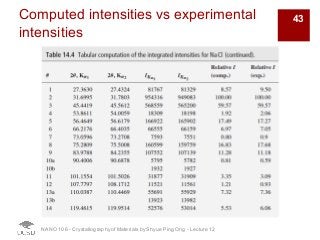
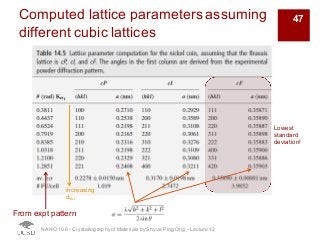
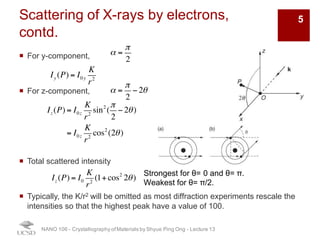
The document discusses X-ray diffraction in the context of crystallography, focusing on how X-rays scatter off electrons in an atom and the implications for measuring intensities and understanding material structures. It details various scattering phenomena, including Thomson and Compton scattering, and explains the significance of systematic extinctions and the structure factor in diffraction patterns. Additionally, it covers practical calculations and factors affecting measured diffraction intensities such as temperature and absorption.












![Structure factor for primitive lattice
¡ For a primitive lattice, there are no other symmetrically
equivalent atoms in the unit cell.
¡ If we only have a single atom in the unit cell at r = (0, 0, 0)
[note we have dropped the functional dependence of f for
brevity]
¡ Note that f does depend on the lattice plane (hkl) through
the dependence on θ.
¡ No extinctions and all planes give rise to diffracted beam.
NANO 106 - Crystallography ofMaterials by Shyue Ping Ong - Lecture 12
Fhkl = f
I = f 2
15](https://image.slidesharecdn.com/12-x-raydiffraction-160504134750/85/UCSD-NANO106-12-X-ray-diffraction-15-320.jpg)