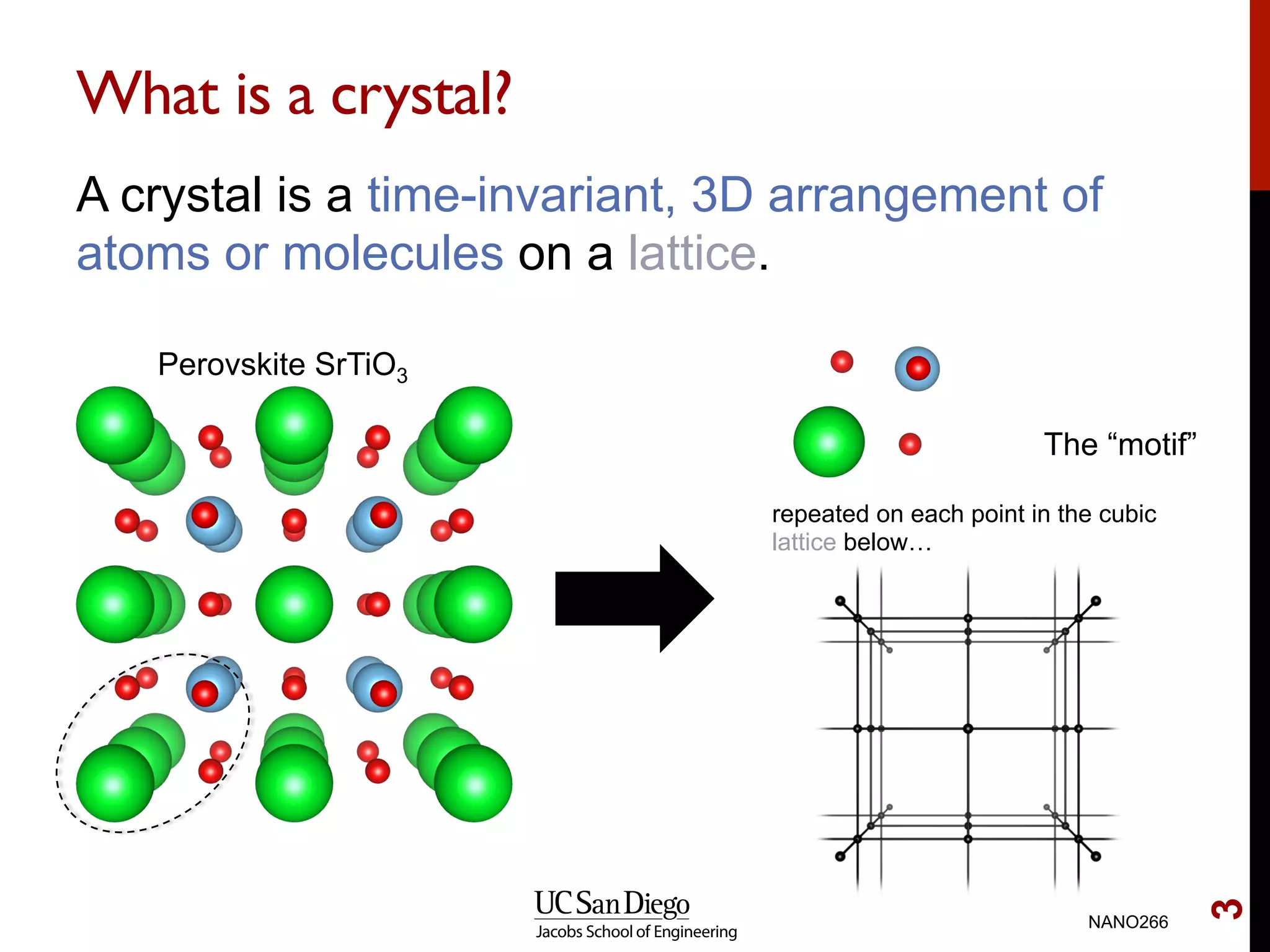
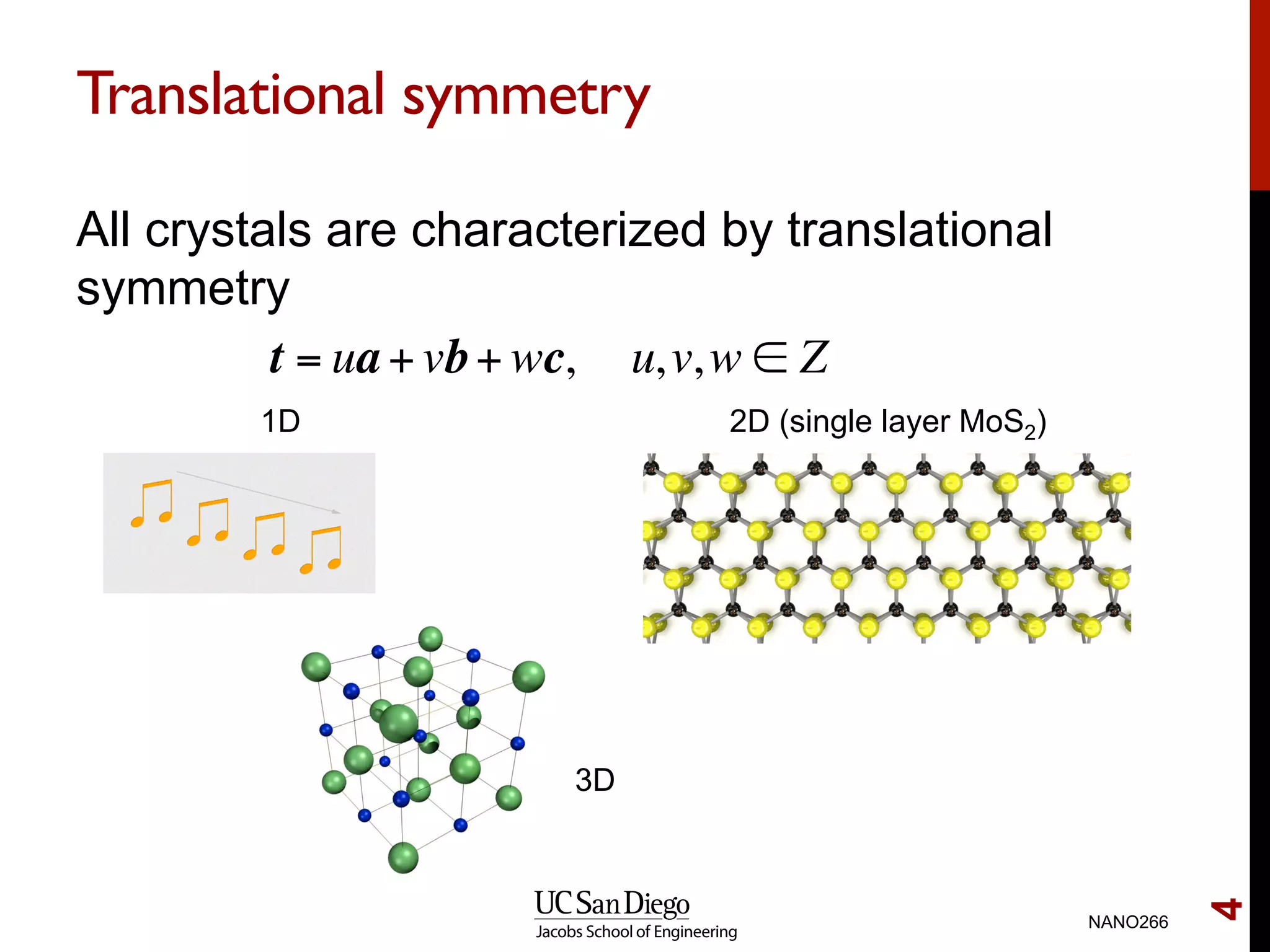
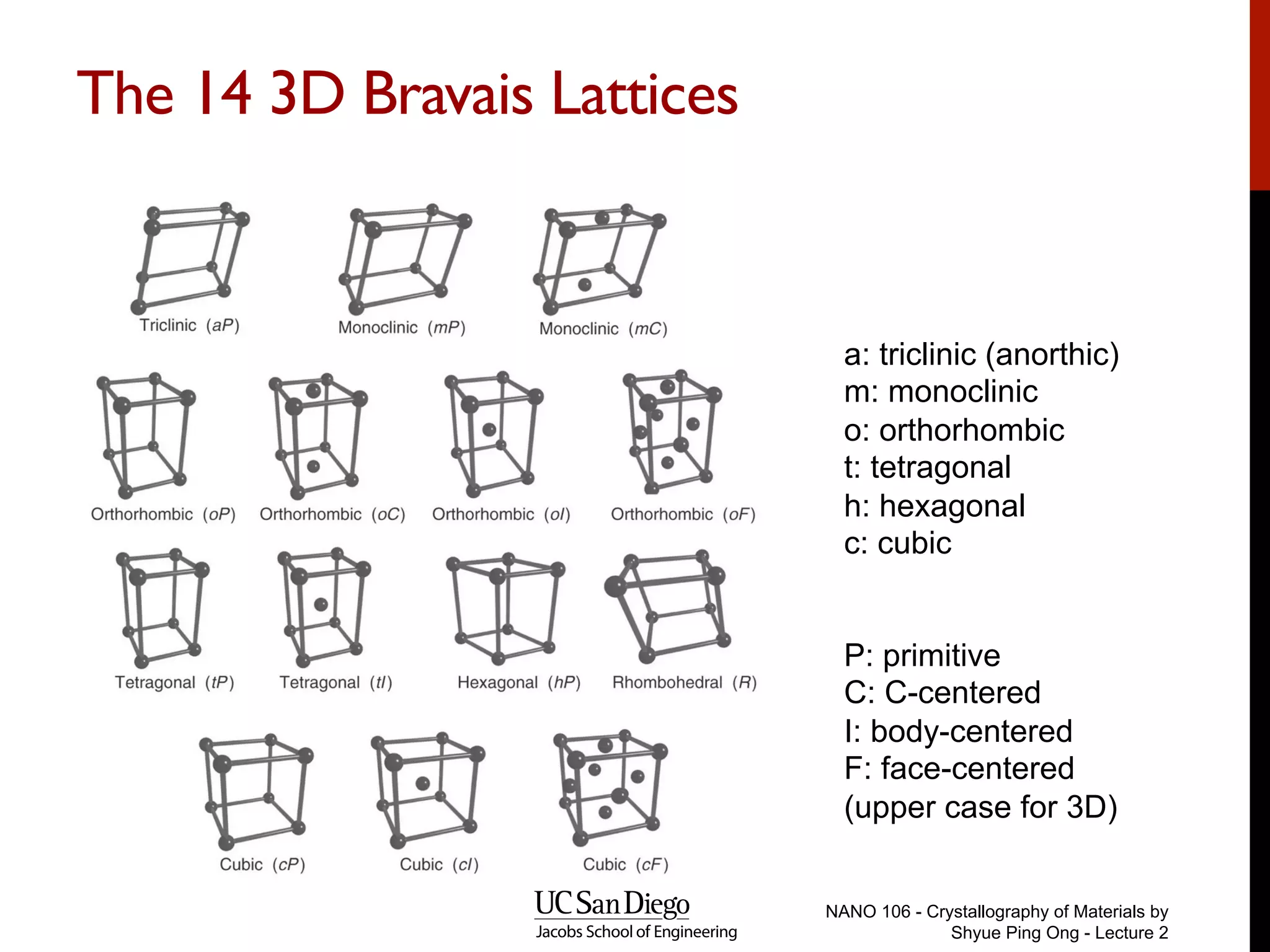
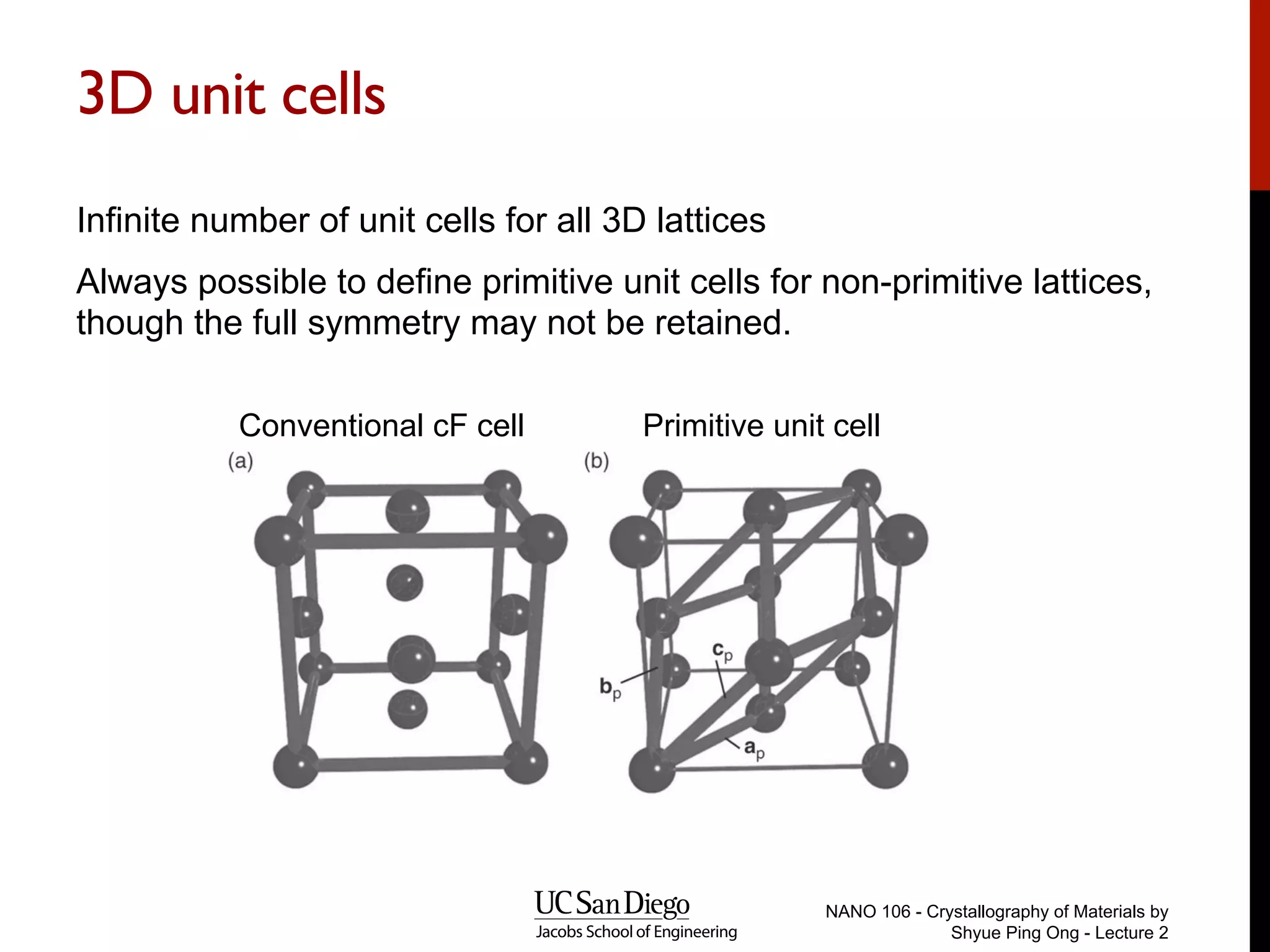
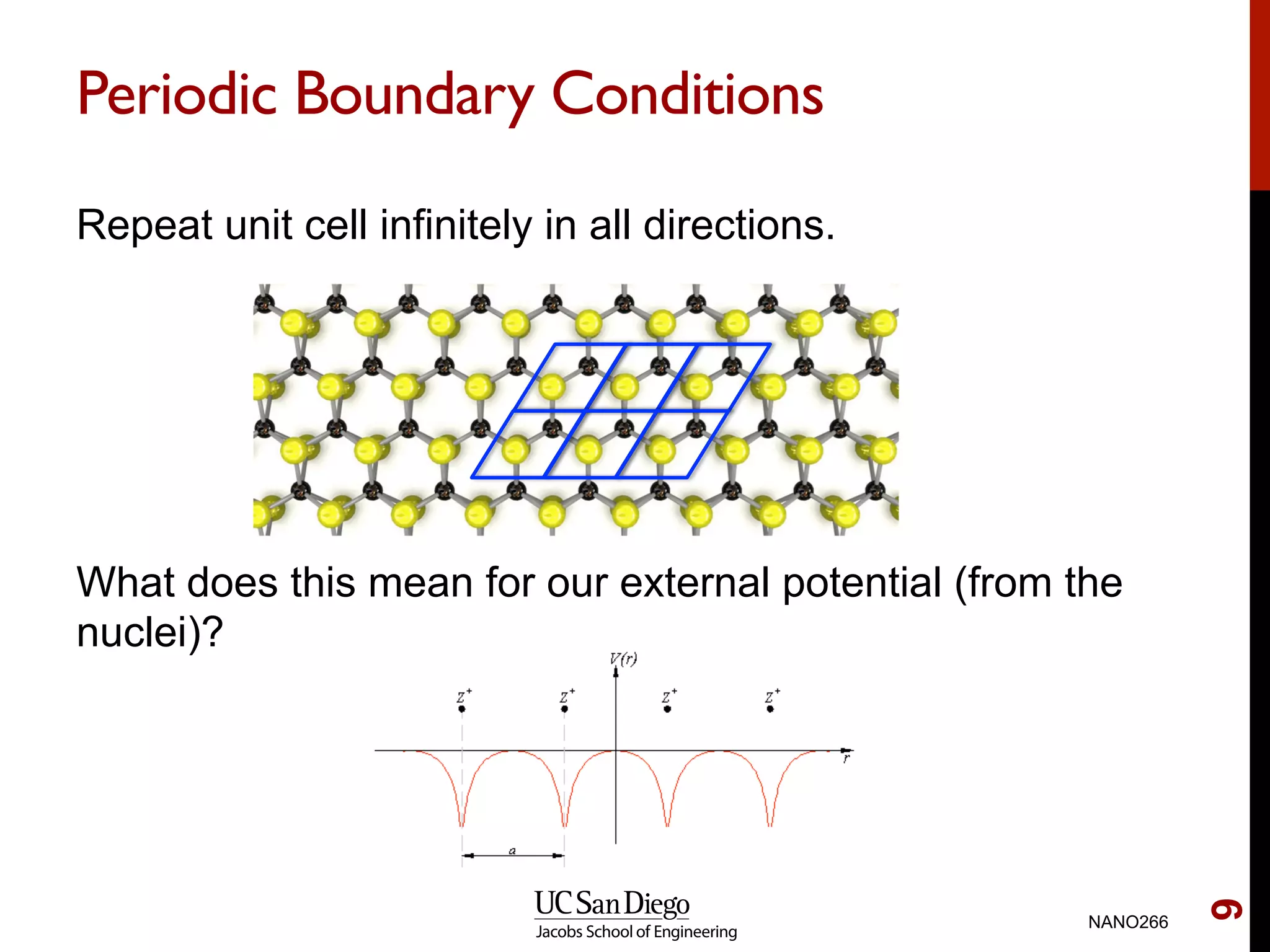
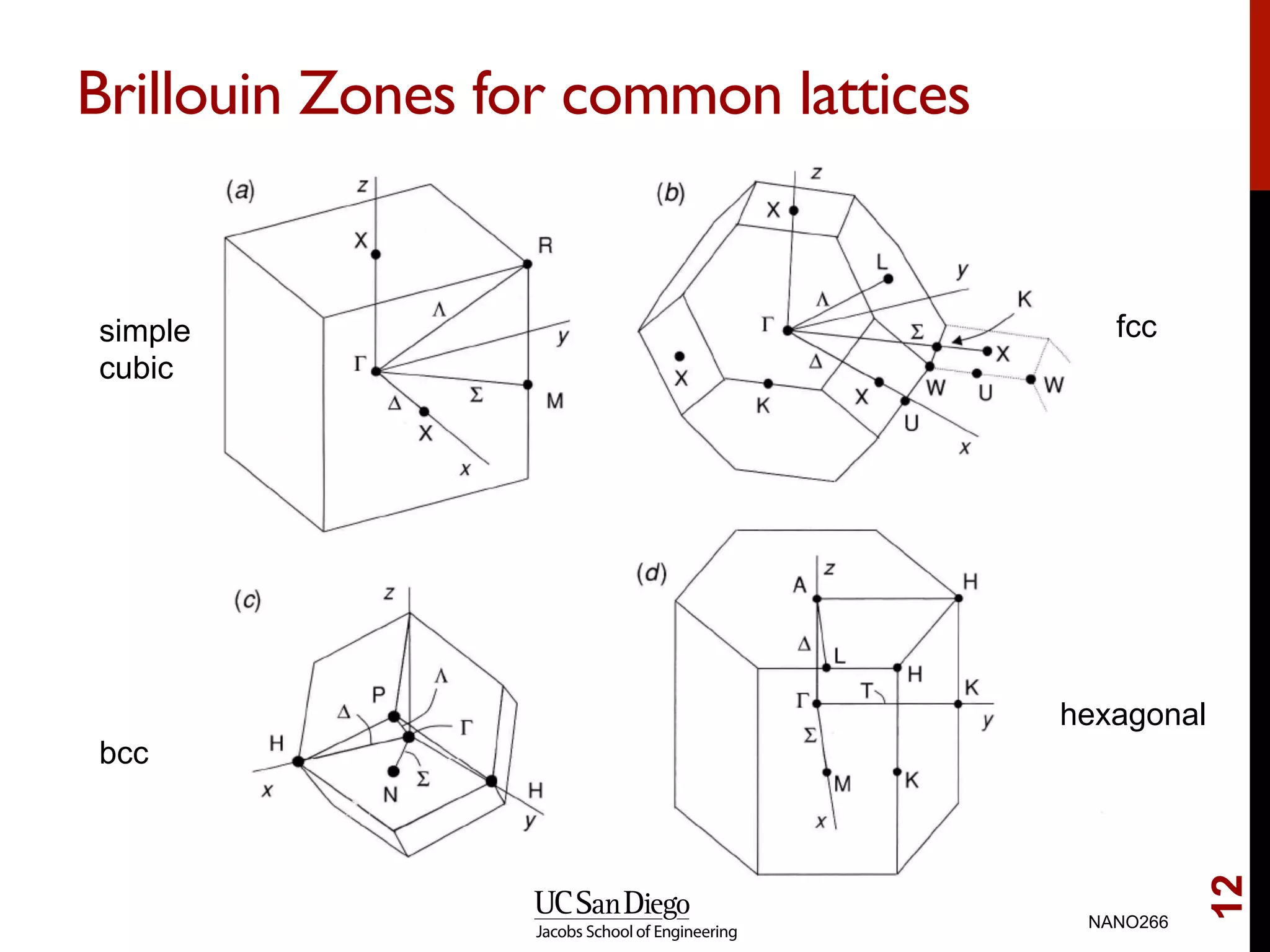
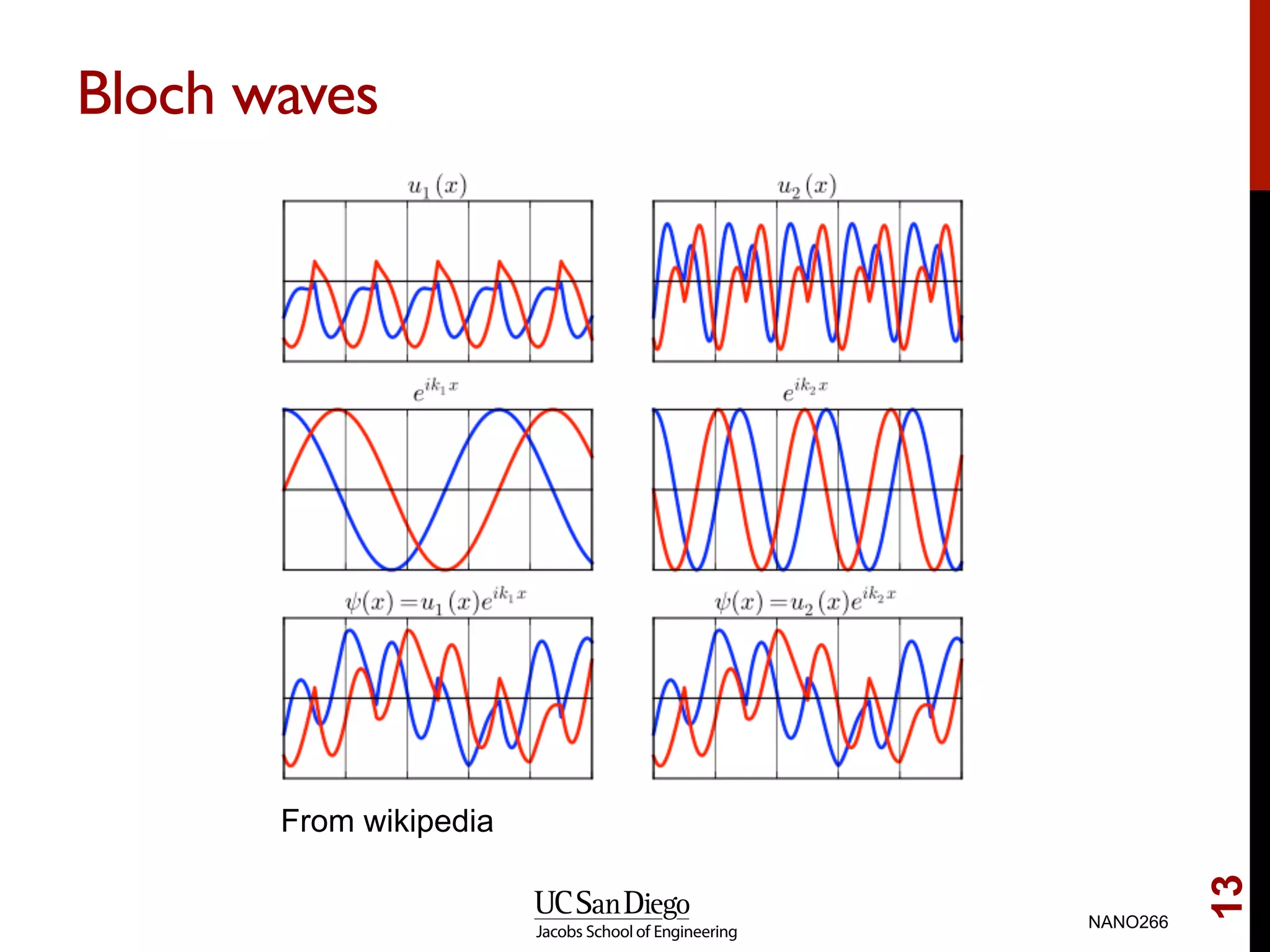
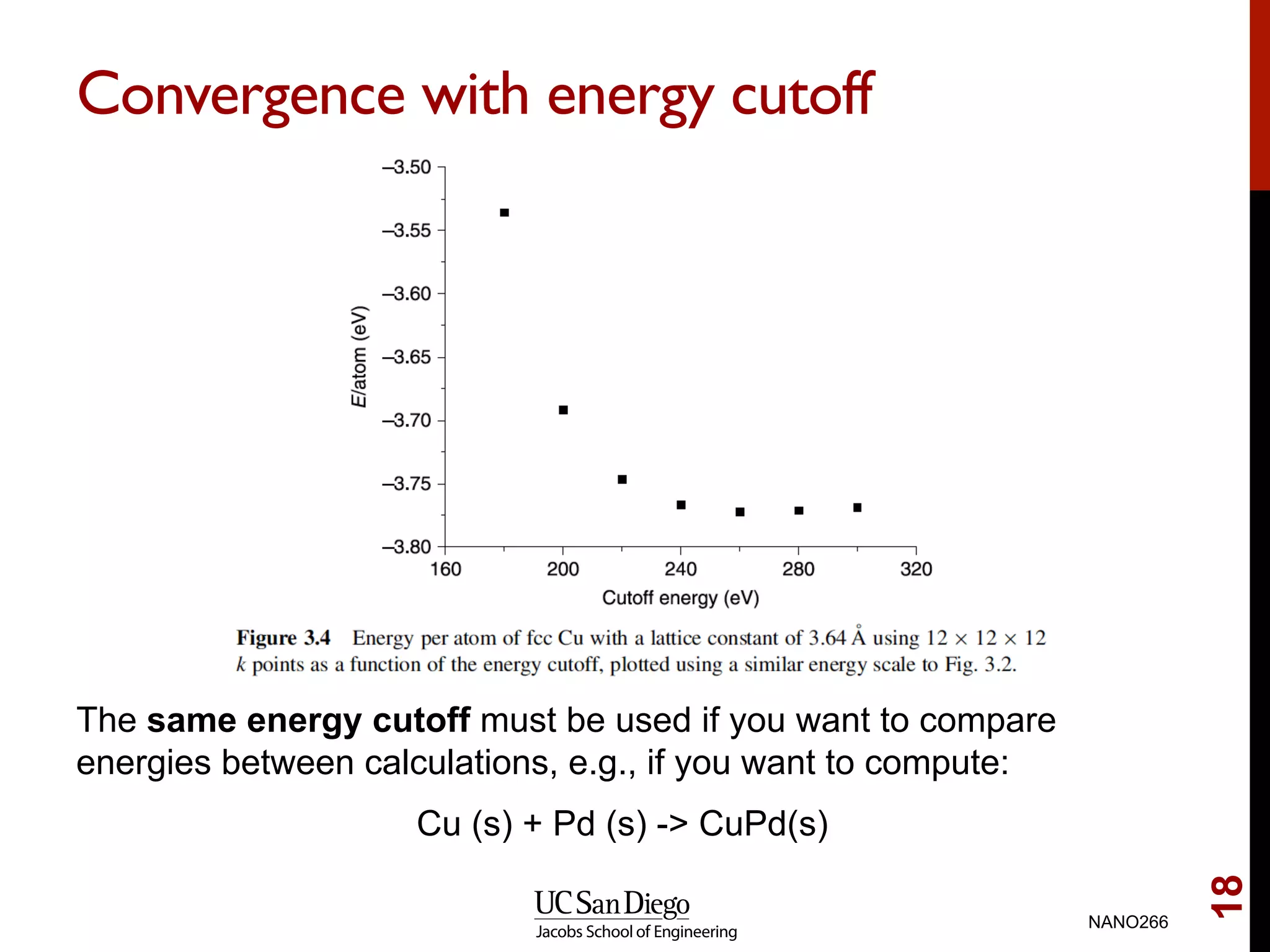
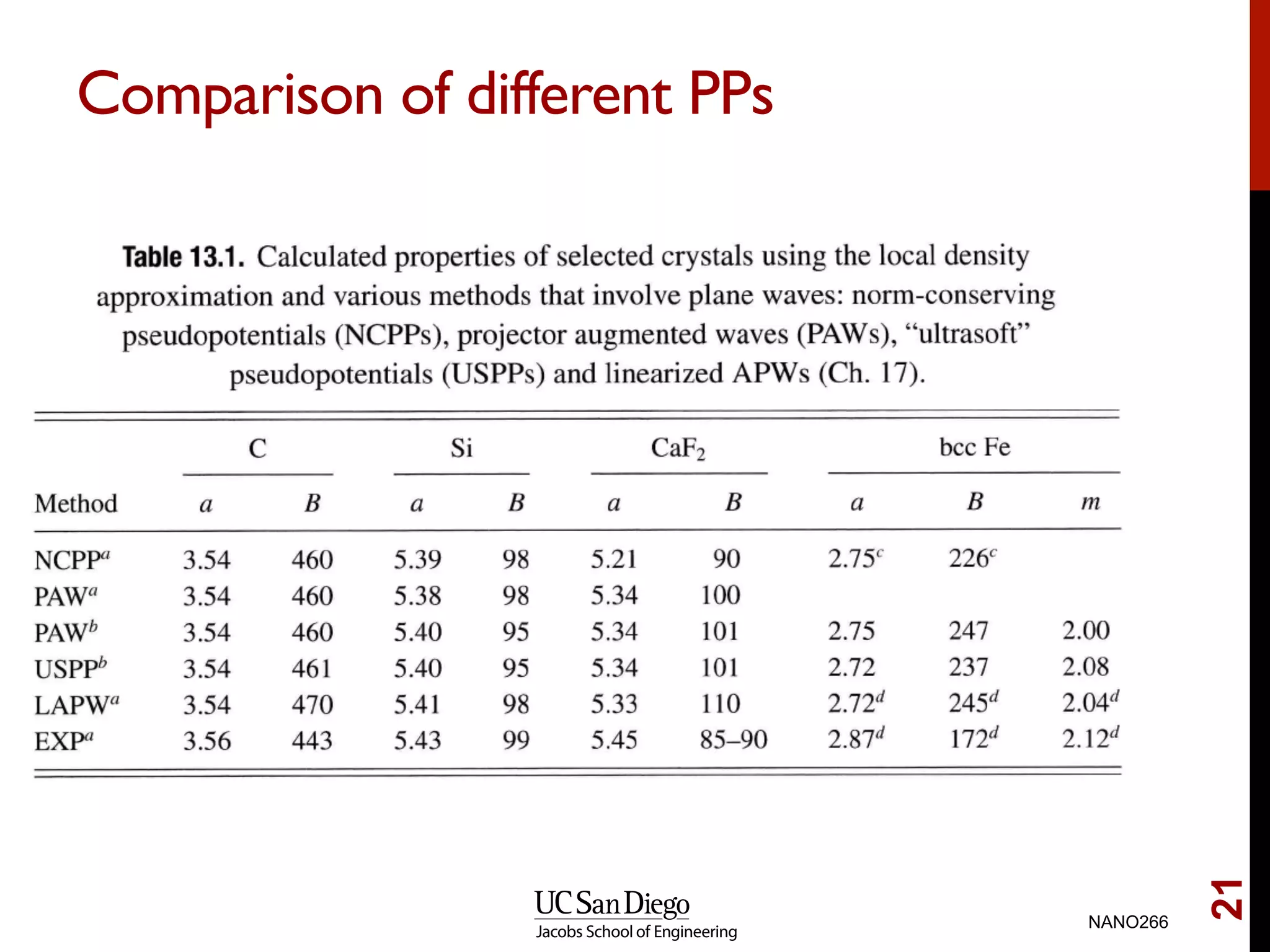
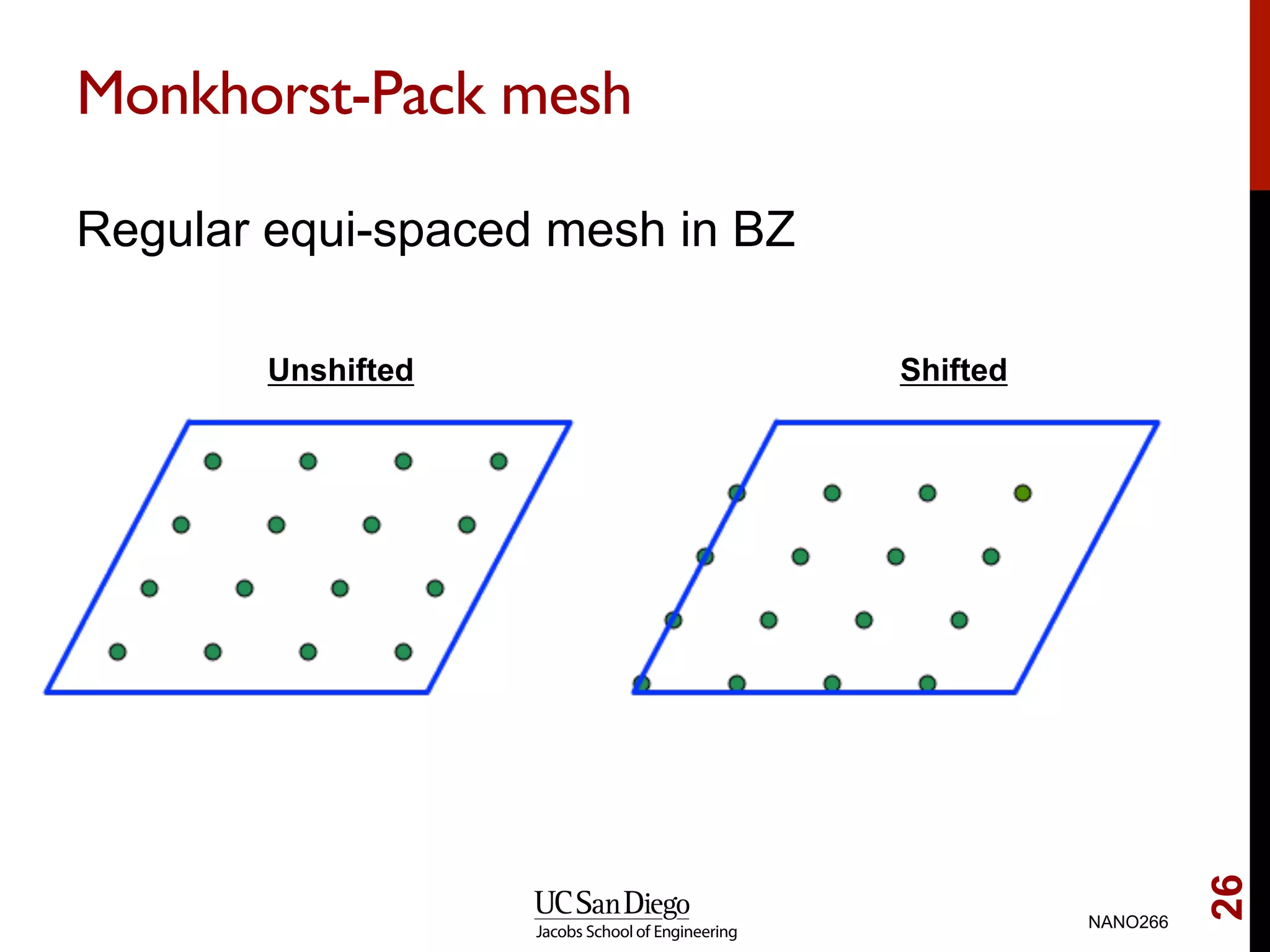
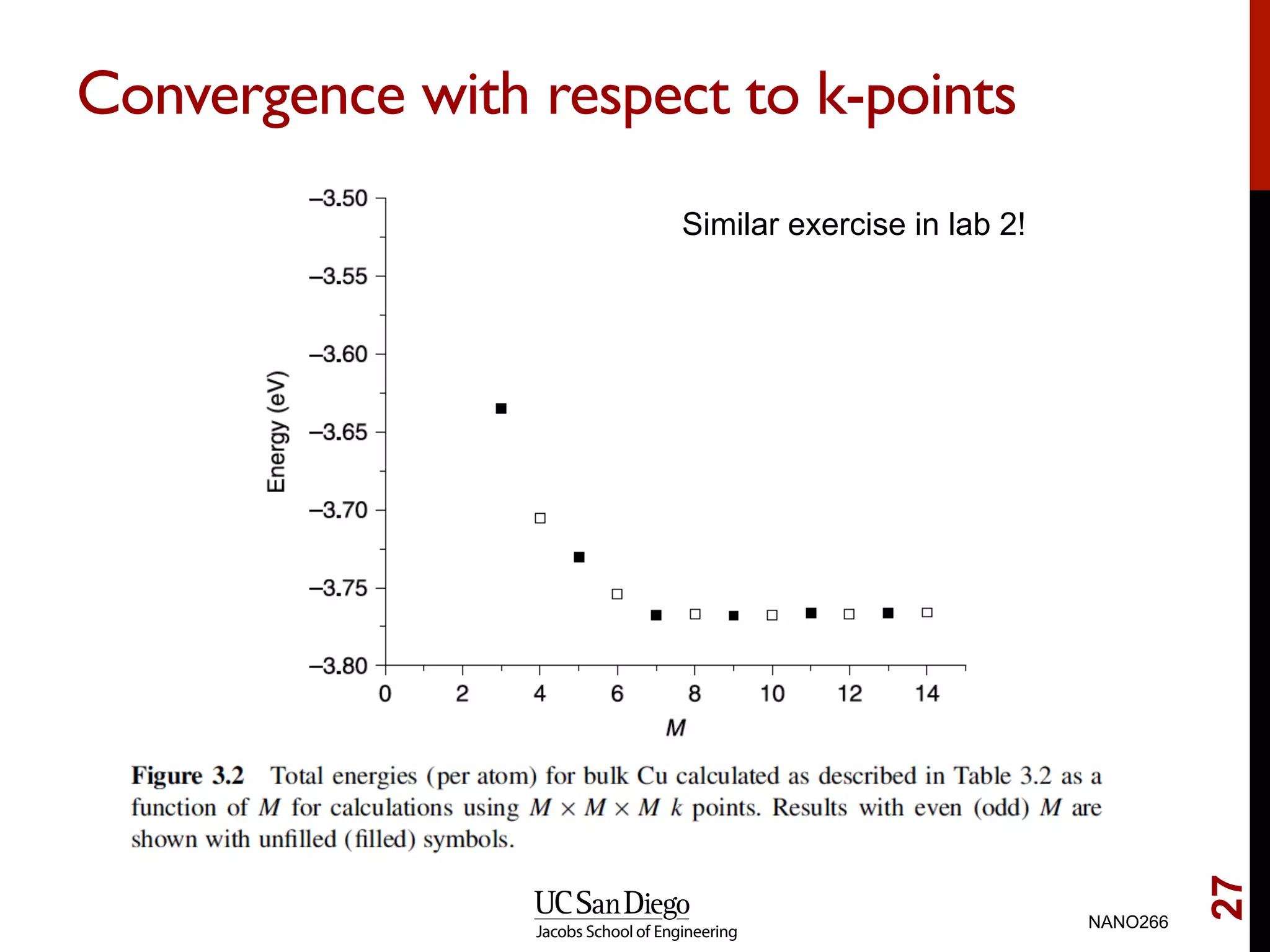
The document discusses quantum mechanical modeling of periodic structures, focusing on crystalline solids and their translational symmetry. It explains concepts such as Bravais lattices, Bloch waves, and the reciprocal lattice while introducing pseudopotentials for approximating electron behavior in crystal structures. Additionally, it covers k-point sampling techniques necessary for accurate calculations in solid-state physics.

1. Quantum Mechanical
Modeling of Periodic
Structures
Shyue Ping Ong

2. The MaterialsWorld
NANO266
2
Molecules
Isolated gas
phase
Typically use
localized basis
functions, e.g.,
Gaussians
Everything else
(liquids,
amorphous solids,
etc.)
Too complex
for direct QM!
(at the
moment)
But can work
reasonable
models
sometimes
Crystalline solids
Periodic
infinite solid
Plane-wave
approaches

3. What is a crystal?
A crystal is a time-invariant, 3D arrangement of
atoms or molecules on a lattice.
NANO266
Perovskite SrTiO3
The “motif”
repeated on each point in the cubic
lattice below…
3

4. Translational symmetry
All crystals are characterized by translational
symmetry
NANO266
4
t = ua + vb + wc, u,v,w ∈ Z
1D 2D (single layer MoS2)
3D

5. The 14 3D Bravais Lattices
NANO 106 - Crystallography of Materials by
Shyue Ping Ong - Lecture 2
P: primitive
C: C-centered
I: body-centered
F: face-centered
(upper case for 3D)
a: triclinic (anorthic)
m: monoclinic
o: orthorhombic
t: tetragonal
h: hexagonal
c: cubic

6. 3D unit cells
Infinite number of unit cells for all 3D lattices
Always possible to define primitive unit cells for non-primitive lattices,
though the full symmetry may not be retained.
NANO 106 - Crystallography of Materials by
Shyue Ping Ong - Lecture 2
Conventional cF cell Primitive unit cell

7. The Reciprocal Lattice
For a lattice given by basis vectors a1, a2 and a3, the
reciprocal lattice is given basis vectors a1*, a2* and a3*
where:
NANO 106 - Crystallography of Materials by
Shyue Ping Ong - Lecture 2
a1
*
= 2π
a2 × a3
a1.(a2 × a3 )
a2
*
= 2π
a1 × a3
a1.(a2 × a3 )
a3
*
= 2π
(a1 × a2 )
a1.(a2 × a3 )
ai
*
aj = 2πδij

8. Reciprocal lattice
Translation vectors in the reciprocal lattice is given by:
NANO266
8
G = ha1
*
+ ka2
*
+la3
*
Direct lattice Reciprocal lattice
Simple Cubic Simple Cubic
Face-centered cubic (fcc) Body-centered cubic (bcc)
Body-centered cubic (bcc) Face-centered cubic (fcc)
Hexagonal Hexagonal

9. Periodic Boundary Conditions
Repeat unit cell infinitely in all directions.
What does this mean for our external potential (from the
nuclei)?
NANO266
9

10. Electron in a periodic potential
For an electron in a 1D periodic potential with lattice
vector a, we have
For any periodic function, we may express it in terms of a
Fourier series
NANO266
10
H = −
1
2
∇+V(x)
where V(x) =V(x + ma).
V(x) = Vne
i
2π
a
nx
n=−∞
∞
∑

11. Bloch’sTheorem
For a particle in a periodic potential, eigenstates can be written in the
form of a Bloch wave
Where u(r) has the same periodicity as the crystal and k is a vector of
real numbers known as the crystal wave vector, n is known as the
band index.
For any reciprocal lattice vector K, , i.e.,
we only need to care about k in the first Brillouin Zone
NANO266
11
ψn,k (r) = eik.r
un,k (r)
Plane wave
ψn,k+K (r) =ψn,k (r)

12. Brillouin Zones for common lattices
NANO266
12
simple
cubic
fcc
bcc
hexagonal

13. Bloch waves
NANO266
13
From wikipedia

14. Plane waves as a basis
Any function that is periodic in the lattice can be written as a
Fourier series of the reciprocal lattice
Recall that from the Bloch Theorem, our wave function is of the
form
Where u(r) has the same periodicity as the crystal and k is a
vector of real numbers known as the crystal wave vector, n is
known as the band index.
NANO266
14
ψn,k (r) = eik.r
un,k (r)
f (x) = cne
i
2π
a
nx
n=−∞
∞
∑
Reciprocal lattice vector in 1D

15. Plane waves as a basis
Let us now write u(r) as an expansion
Our wave function then becomes
NANO266
15
un,k (r) = cG
n,keiGr
G
∑
ψn,k (r) = cG
n,kei(k+G).r
G
∑

16. Using the plane waves as basis
Plane waves offer a systematic way to improve
completeness of our solution
Recall that for a free electron in a box,
Corresponding, each plane wave have energy
NANO266
16
ψn,k (r) = cG
n,kei(k+G).r
G
∑
Infinite sum over reciprocal space
ψ(r) = eik.r
and the corresponding energy is E =
!2
2m
k2
E =
!2
2m
k+G
2

17. Energy cutoff
Solutions with lower energy are more physically
important than solutions with higher energies
NANO266
17
Ecut =
!2
2m
Gcut
2
ψn,k (r) = cG
n,kei(k+G).r
k+G<Gcut
∑

18. Convergence with energy cutoff
The same energy cutoff must be used if you want to compare
energies between calculations, e.g., if you want to compute:
Cu (s) + Pd (s) -> CuPd(s)
NANO266
18

19. Pseudopotentials
Problem: Tightly bound electrons
have wavefunctions that
oscillate on very short length
scales => Need a huge cutoff
(and lots of plane waves).
Solution: Pseudopotentials to
represent core electrons with a
smoothed density to match
various important physical and
mathematical properties of true
ion core
NANO266
19
ψn,k (r) = cG
n,kei(k+G).r
G
∑

20. Types of pseudopotentials (PPs)
Norm-conserving (NC)
• Enforces that inside cut-off radius, the norm of the pseudo-wavefunction
is identical to all-electron wavefunction.
Ultrasoft (US)
• Relax NC condition to reduce basis set size further
Projector-augmented wave (PAW)
• Avoid some problems with USPP
• Generally gives similar results as USPP and all-electron in many
instances.
NANO266
20
Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B, 1999, 59, 1758–1775.

21. Comparison of different PPs
NANO266
21

22. How do you choose PPs?
Sometimes, several PPs are available with different
number of “valence” electrons, i.e., electrons not in
the core.
Choice depends on research problem – if you are
studying problems where more (semi-core) electrons
are required, choose PP with more electrons
But more electrons != better results! (e.g., Rare-earth
elements)
NANO266
22

23. Born–von Karman boundary condition
Consider large, but finite crystal of volume V with edges
Born-von Karman boundary condition requires
Since we have Bloch wavefunctions,
Therefore, possible k-vectors compatible with cyclic boundaries are
given by:
NANO266
23
N1t1, N2t2, N3t3
ψ(r+ N1t1 ) =ψ(r+ N2t2 ) =ψ(r+ N3t3) =ψ(r)
eikN1t1
= eikN2t2
= eikN3t3
=1
k =
m1
N1
g1 +
m2
N2
g2 +
m3
N3
g3

24. Integrations in k space
For counting of electrons in bands and total energies, etc.,
need to sum over states labeled by k
Numerically, integrals are performed by evaluating
function at various points in the space and summing them.
NANO266
24
f =
Vcell
(2π)3
f (k)dk
BZ
∫
f =
1
Nk
f (k)
k
∑

25. Choice of k-points
1. Sampling at one point (Baldereschi point, or
Gamma point)
2. Monkhorst-Pack – Sampling at regular
meshes
NANO266
25

26. Monkhorst-Pack mesh
Regular equi-spaced mesh in BZ
NANO266
26
Unshifted Shifted

27. Convergence with respect to k-points
NANO266
27
Similar exercise in lab 2!

28. Important things to note about k-point
convergence
Symmetry reduces integrals to be performed ->
Irreducible Brillouin Zone
k-point mesh is inversely related to unit cell volume (larger
unit cell volume -> smaller reciprocal cell volume)
NANO266
28

29. k-point sampling in metals
BZ in metals are divided into occupied and
unoccupied regions by Fermi surface, where
the integrated functions change
discontinuously from non-zero to zero. =>
Extremely dense k-point mesh needed for
integration
Algorithmic solutions
• Tetrahedron method. Use k points to
define a tetrahedra that fill reciprocal
space and interpolate. Most widely
used is Blochl’s version.
• Smearing. Force the function being
integrated to be continuous by
“smearing” out the discontinuity, e.g.,
with the Fermi-Dirac function or the
Methfessel and Paxton method.
NANO266
29
Fermi-surface of Copper (Cu), the
color codes the inverse effective
mass of the electrons, large effective
masses are represented in red, from
A. Weismann et al., Science 323,
1190 (2009)

30. References
Martin, R. M. Electronic Structure: Basic Theory
and Practical Methods (Vol 1); Cambridge
University Press, 2004.
Grosso, G.; Parravicini, G. P. Solid State
Physics: : 9780123044600: Amazon.com: Books;
1st ed.; Academic Press, 2000.
NANO266
30