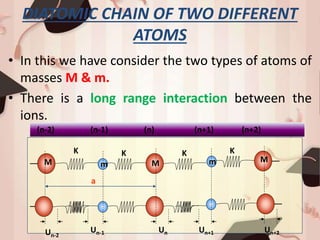
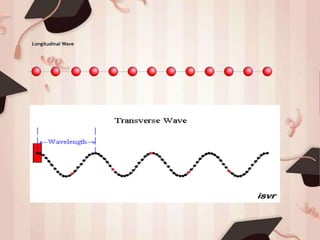
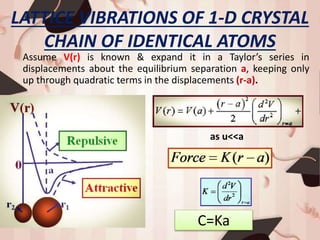
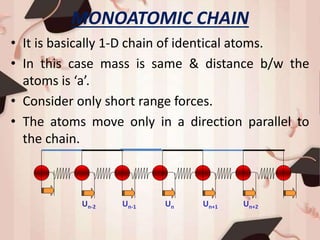
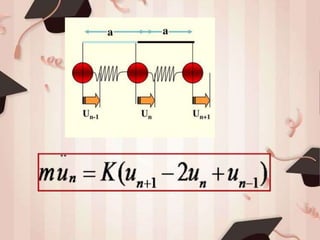
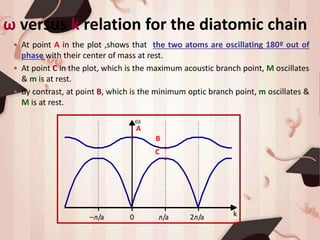
1) The document discusses lattice dynamics and lattice vibrations, focusing on 1D monoatomic and diatomic crystal chains. 2) For a monoatomic chain, the equation of motion results in a dispersion relation of ω=Ck, where C is the speed of sound waves. 3) For a diatomic chain with atoms of masses M and m, the equations of motion yield a quadratic dispersion relation. This results in acoustic and optical branches corresponding to in-phase and out-of-phase vibrations of the atoms.

1. LATTICE
DYNAMICS

2. BASIC DEFINATIONS
HOOK’S LAW
ACOUSTIC/OPTICAL BRANCHES
ZERO POINT ENERGY
HARMONIC LIMIT
LATTICE DYNAMICS
LATTICE VIBRATIONS

3. STRESS & STRAIN
STRESS
IT IS RESTORING FORCE
PER UNIT AREA
ITS UNIT IS N/m2
STRAIN
IT IS CHANGE IN SHAPE
PER ORIGINAL SHAPE
IT HAS NO UNIT

4. HOOKE’S LAW

5. SOUND WAVES
• Sound is defined as Oscillation in pressure, stress,
particle displacement, particle velocity, etc.,
propagated in a medium with internal forces (e.g.,
elastic or viscous), or the superposition of such
propagated oscillation.
• Sound can propagate through a medium such as
air, water and solids as longitudinal wave and also
as a transverse wave in solids.
• Presence of atoms has no significance in this
wavelength limit, since λ>>a, so there will no
scattering due to the presence of atoms.

7. SPEED OF SOUND WAVES
• For fluids in general, the speed of sound c is
• Thus the speed of sound increases with the
stiffness (the resistance of an elastic body to
deformation by an applied force) of the material
and decreases with an increase in density.
L
C
V 

 

8. DISPERSION RELATION
• The relation between the frequency and wave
number is the DISPERSION RELATION.
=v/K
SLOPE REPRESENTS VELOCITY

9. LATTICE VIBRATIONS OF 1-D CRYSTAL
CHAIN OF IDENTICAL ATOMS
Assume V(r) is known & expand it in a Taylor’s series in
displacements about the equilibrium separation a, keeping only
up through quadratic terms in the displacements (r-a).
as u<<a
as u<<a
C=Ka

10. MONOATOMIC CHAIN
• It is basically 1-D chain of identical atoms.
• In this case mass is same & distance b/w the
atoms is ‘a’.
• Consider only short range forces.
• The atoms move only in a direction parallel to
the chain.
Un-2 Un-1 Un Un+1 Un+2

12. • The total force on the nth atom is the sum of 2
forces.
• The force to the right
• The force to the left
Total Force = Force to right – Force to left

13. • GENERAL EQUATION FOR DISPLACEMENT
• DIFFERENTIATE THE ABOVE EQUATION
UNDISPLAYED POSITION :-
DISPLAYED POSITION:-

14.        
 
0 0 0 0
1 12
e e 2 e e
n n n ni kx t i kx t i kx t i kx t
m K A A AA
   
 
    
  
       
 2
e e 2 e e
i kna t i kna ka t i kna t i kna ka t
m K A A AA
   

     
   
       
 2
e e e 2 e e e
ika ikai kna t i kna t i kna t i kna t
m K A A AA
   

   
   
CANCEL THE COMMON TERM WE GET FINAL EQUATION
 2 e 2 eika ika
m K 
   

15. • MAX POSSIBLE VALUE OF sin(ka/2)=1
 do not depend on n (i.e) correspond to each k
there is definite .
• FOR LONGITUDINAL

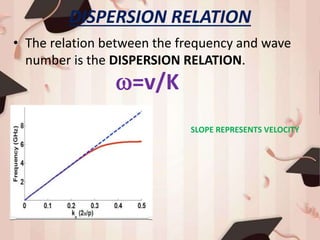
16. ω versus k relation for the monatomic
chain
max 2
/s
K
m
V k




[-(π/a)  k  (π/a)]

17. • Points A & C are symmetrically equivalent. They
have thesame frequency & the same atomic
displacements.
• The group velocity vg = (dω/dk) at both of them
is negative, so that a wave at that ω & that k
moves to the left. Point B in the ω(k) diagram
has the same frequency & displacement as points
A and C, but vg = (dω/dk) there is positive, so
that a wave at that ω & that k moves to the right.
• Adding a multiple of 2π/a to k does not change either
ω or vg, sopoint A contains no physical information that
is different point B.

18. DIATOMIC CHAIN OF TWO DIFFERENT
ATOMS
• In this we have consider the two types of atoms of
masses M & m.
• There is a long range interaction between the
ions.
(n-2) (n-1) (n) (n+1) (n+2)
Un-2
Un-1 Un Un+1 Un+2
K K K K
M Mm
Mm
a

19. • Since there is two atoms of different masses so
there are two equations of motion
Equation of Motion for M

Equation of Motion for m

..
1 1( ) ( )n n n n nM u K u u K u u    
1 1( 2 )n n nK u u u   
..
1 1 2( ) ( )n n n n nmu K u u K u u     
..
1 2( 2 )n n n nmu K u u u   

20. m m
Un-1 Un Un+1 Un+2
M
Un-2
M M
0
/ 2nx na 0
expn nu A i kx t   
Displacement for M

 0
expn nu A i kx t    
Displacement for m

 
..
2 0
expn nu A i kx t     
GENERAL EQUATION

21.    1 1
2 22 2 2
2
k n a k n akna knai t i ti t i t
MAe K Ae Ae Ae
  
  
               
       
 
    
 
 
2 2 2 2 22 2
2
kna kna kna knaka kai t i t i t i ti i
MAe K Ae e Ae Ae e
   
  
       
           
       
 
    
 
 
CANCEL THE COMMON TERM WE GET FINAL EQUATION
2 2 2
2
ka ka
i i
M K e e  
 
    
 
2
2 1 cos
2
ka
M K 
 
  
 
Equation of Motion for the nth Atom (M)

22.      1 1 2
2 2 22 2
2
k n a k n a k n aknai t i t i ti t
A me K Ae Ae Ae
  
  
                
       
 
    
 
 
2
2 2 2 2 22 2 2
2
kna kna kna knaka ka kai t i t i t i ti i i
mAe e K Ae Ae e Ae e
   
 
       
            
       
 
    
 
 
2
2 cos
2
ka
m K 
 
   
 
CANCEL THE COMMON TERM WE GET FINAL EQUATION
Equation of Motion for the (n-1)th Atom (m)

23. • The Equation for M becomes:
• The Equation for m becomes:
• FOR CALCULATING THE VALUE OF 

24. • So, the resulting quadratic equation for ω2 is:
• The two solutions for ω2 are:

25. ω versus k relation for the diatomic chain
• At point A in the plot ,shows that the two atoms are oscillating 180º out of
phase with their center of mass at rest.
• At point C in the plot, which is the maximum acoustic branch point, M oscillates
& m is at rest.
• By contrast, at point B, which is the minimum optic branch point, m oscillates &
M is at rest.
0 л/a 2л/a–л/a k

A
B
C