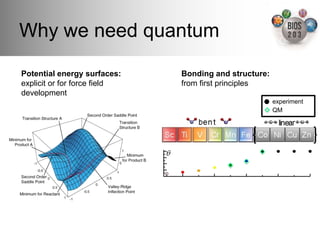
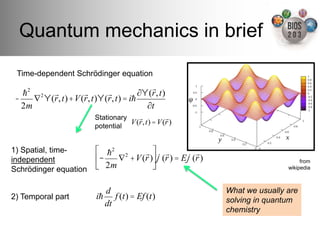
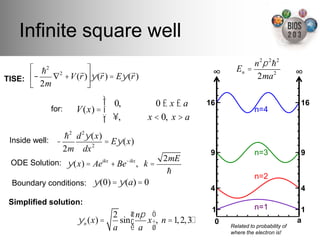
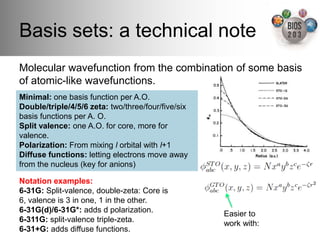
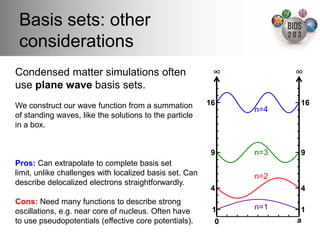
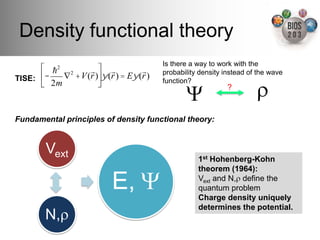
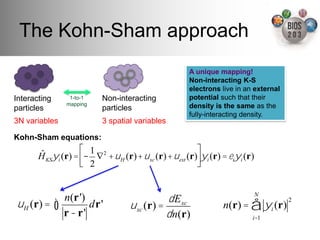
The document serves as an introduction to electronic structure theory, discussing the necessity of quantum mechanics in understanding phenomena like optical and magnetic properties, and the role of potential energy surfaces. It outlines key concepts such as the Schrödinger equation, Hartree-Fock equations, and Density Functional Theory (DFT), highlighting the challenges in calculating electron correlations and approximating energy states. Additionally, it provides references for further reading on quantum mechanics and electronic structure methods.







![Variational Principle!
ˆ | !#
"! | H
E[!] =
"! | !#
Energy of a trial wavefunction is greater Unless the trial wavefunction is
than the energy of the exact solution:! the exact solution:!
E[!] " E0 E[!] = E0
If we have the ground state energy, we have the ground
state wavefunction.!](https://image.slidesharecdn.com/bios203-lect2-130201201936-phpapp01/85/BIOS-203-Lecture-2-introduction-to-electronic-structure-theory-11-320.jpg)


![Hartree-Fock Equations!
With a Slater determinant wavefunction to represent our many-body
wavefunction:! ! ! !
! (r ) ! (r ) " ! (r )
! ! ! !
! !
"
!
1 ! (r ) ! (r ) " ! (r )
1 " 1 " 1
" 2 " 2 " 2
! ! (r , r ,…, r ) =
n!
1
"
2 n
" # "
! ! !
! (r ) ! (r ) " ! (r )
! " n " n " n
We may now obtain analogous Hartree-Fock equations:!
Standard notation! Bra-ket notation!
$ 1 2 ! !' ! Coulomb integral!
&! "i + #V ( RI ! ri ))! " (ri ) + 1-electron integrals! ˆ
Jij = ! i! j " ee ! i! j
% 2 I (
"i2 Exchange integral!
$ hi = ! i ! +Ve!N ! i
* ! 1 ! !' ! 2 ˆ
K ij = ! i! j " ee ! j! i
&# * ! µ (rj ) ! ! ! µ (rj )drj )! " (ri ) !
&µ
% rj ! ri )
(
$ N N!1 N
! 1 ! !' ! ! ˆ
ESlater [! ] = ! Slater H ! Slater = " hi + " " ( Jij ! K ij )
#& * ! µ* (rj ) ! !
rj ! ri
! " (rj )drj )! µ (ri ) = !" # (ri )
µ &
% )
( i=1 i=1 j=i+1
Pros: Anti-symmetrized, exchange is exact.!
Cons: Only correlation comes from anti-symmetrized Slater.!](https://image.slidesharecdn.com/bios203-lect2-130201201936-phpapp01/85/BIOS-203-Lecture-2-introduction-to-electronic-structure-theory-14-320.jpg)




![2nd Hohenberg-Kohn theorem!
A variational principle for DFT:"
! ! ! ! !
Ev [ ! '(r )] = F[ ! '(r )]+ ! vext (r )! '(r )dr " E0
Trial wavefunction
from trial density:" Our universal Energy of the
functional with an exact solution."
Ψ
ρ
initial guess."
BUT we still donʼt know what our functional form is!!](https://image.slidesharecdn.com/bios203-lect2-130201201936-phpapp01/85/BIOS-203-Lecture-2-introduction-to-electronic-structure-theory-22-320.jpg)
![Exc: Exchange & Correlation!
In principle, DFT is exact…"
" ! E xc
…but we need the dependence ! xc (r) =
of Exc with our density." ! n(r)
What is Exc?!
E xc [ ! (r)] = !T [ ! (r)] + !Vee [ ! (r)]
Correction to Non-classical
kinetic energy corrections to
from interacting electron-electron
nature of electrons" repulsion"](https://image.slidesharecdn.com/bios203-lect2-130201201936-phpapp01/85/BIOS-203-Lecture-2-introduction-to-electronic-structure-theory-24-320.jpg)
![Understanding our Exc!
Typically model exchange and correlation separately. !
!
Exchange-correlation hole is often fit in terms of model system. This is
the space whereby other electrons are excluded around a given electron.!
"
Local density approximation:"
!
Exchange modeled on HEG ! ! !Correlation on HEG!
!
1/3
! LDA 3" 3 % high limit! ! c = A ln(rs ) + B + rs (C ln(rs ) + D)
E x [ ! ] = ! $ ' ( ! (r)4/3 dr
! 4#" &
!
1 ! g0 g1 $
! low limit! ! c = # + 3/2 +... &
2 " rs rs %
Correlated quantum chemical techniques are used
to interpolate between these limits!](https://image.slidesharecdn.com/bios203-lect2-130201201936-phpapp01/85/BIOS-203-Lecture-2-introduction-to-electronic-structure-theory-25-320.jpg)


