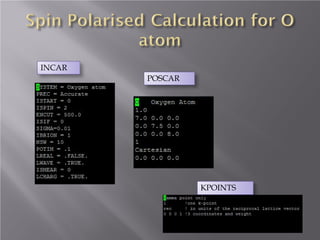
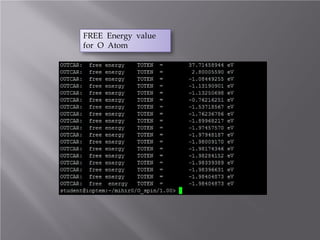
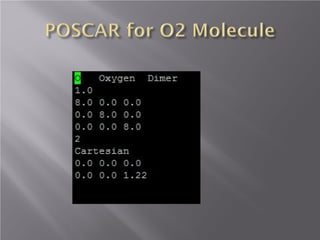
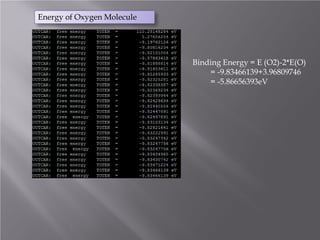
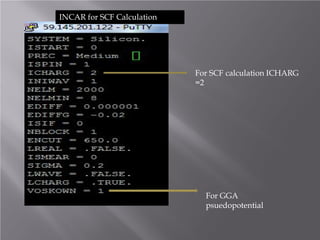
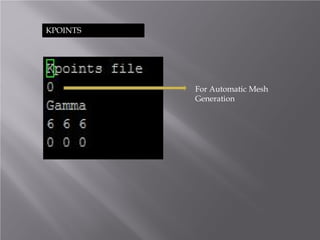
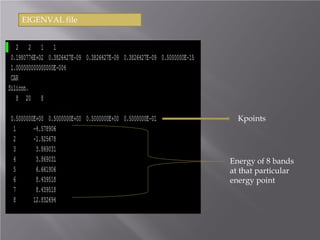
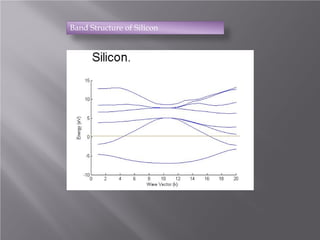
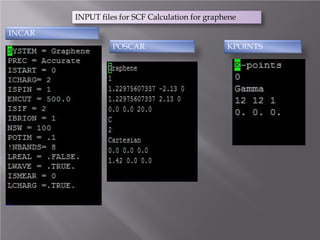
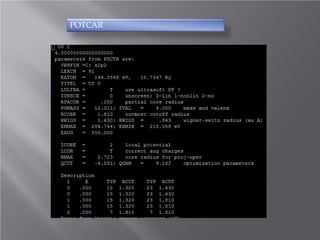
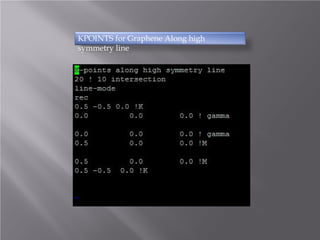
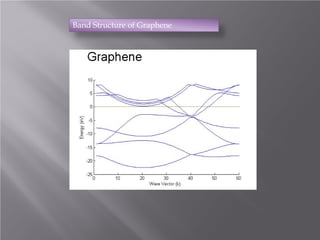
The document discusses density functional theory (DFT) and its implementation in the VASP software. It explains key concepts like the Kohn-Sham approach for approximating the many-body Schrodinger equation and the use of pseudopotentials and plane wave basis sets. It also summarizes some example calculations done in VASP like determining the binding energy of O2, equilibrium lattice constant of Cu, and band structures of Si and graphene. Key input and output files of VASP are also outlined.

1. Mihir
IIT,Bhubaneswar

3. Quantum Mechanical Wave Function gives all information about a
given system.
For a Hydrogen Atom, We can solve Schrodinger Equation exactly and
determine the allowed energy state of the System.
It is difficult to solve Schrodinger Equation for N- body System. We must
involve some approximation for the solution .

4. . It is a method of obtaining an approximate solution
to Schrodinger Equation for many body system.
. It is Primarily a theory of Electronic ground state
structure in terms of electronic density distribution
n(r).

5. The Time independent Schrodinger Equation
H𝞇𝞇 𝑥𝑥1 , 𝑥𝑥2 , … . . 𝑥𝑥 𝑁𝑁 . 𝑅𝑅1 . 𝑅𝑅2 … . . 𝑅𝑅 𝑀𝑀 = 𝐸𝐸𝐸𝐸 (𝑥𝑥1 , 𝑥𝑥2 , . 𝑥𝑥 𝑁𝑁 , 𝑅𝑅1 … … 𝑅𝑅 𝑀𝑀 )
Where H is the Hamiltonian for a system consisting of M
nuclei and N electrons.
1
1
1
2
2
𝐻𝐻 = −
� 𝞩𝞩 𝑖𝑖 −
� 𝞩𝞩𝑗𝑗 + �
2𝑚𝑚 𝑒𝑒
2𝑚𝑚 𝑛𝑛
2
𝑁𝑁
𝑖𝑖=1
𝑁𝑁 𝑀𝑀
𝑀𝑀
𝑗𝑗=1
𝑍𝑍𝑗𝑗 𝑒𝑒
1
+ �
−��
|𝑟𝑟𝑖𝑖 − 𝑟𝑟𝑘𝑘 | 2
𝑖𝑖=1 𝑗𝑗=1
2
𝑀𝑀
𝑗𝑗=1
𝑁𝑁
𝑖𝑖=1
𝑀𝑀
�
𝑤𝑤=1,𝑤𝑤≠𝑗𝑗
𝑁𝑁
�
𝑘𝑘=1,𝑖𝑖≠𝑘𝑘
𝑒𝑒 2
𝑟𝑟𝑖𝑖 − 𝑟𝑟𝑘𝑘
𝑍𝑍𝑗𝑗 𝑍𝑍 𝑤𝑤 𝑒𝑒 2
|𝑟𝑟𝑗𝑗 − 𝑟𝑟𝑤𝑤 |
𝐻𝐻 = 𝑇𝑇𝑒𝑒 + 𝑇𝑇𝑛𝑛 + 𝑉𝑉𝑒𝑒𝑒𝑒 + 𝑉𝑉𝑒𝑒𝑒𝑒 + 𝑉𝑉𝑛𝑛𝑛𝑛

6. First two terms of the above equation are Kinetic Energy of Electrons
and nuclei respectively.
Third term is electron- electron Potential Energy.
Fourth term is the Potential energy between electrons and nuclei.
Last term is nuclei-nuclei potential energy.

7. Born-Oppenheimer
Approximation
𝑚𝑚 𝑛𝑛 ≫ 𝑚𝑚 𝑒𝑒
Nuclei are much slower than electron.
Hence Nuclei Kinetic Energy is zero. 𝑇𝑇𝑛𝑛 = 0
Nuclei-Nuclei Interaction is Constant. 𝑉𝑉𝑛𝑛𝑛𝑛 = 𝐶𝐶𝐶𝐶𝐶𝐶𝐶𝐶𝐶𝐶𝐶𝐶𝐶𝐶𝐶𝐶
Hence we can eliminate the term 𝑇𝑇𝑛𝑛 𝑎𝑎𝑎𝑎𝑎𝑎 𝑉𝑉𝑛𝑛𝑛𝑛 from the
Hamiltonian.
Hence New Hamiltonian for many body system
𝐻𝐻 = 𝑇𝑇𝑒𝑒 + 𝑉𝑉𝑒𝑒 𝑒𝑒 + 𝑉𝑉𝑒𝑒 𝑒𝑒

8. 






All ground state properties are determined by ground
state density n(r).
The total energy of a many body system is a unique
functional of electron density.
Density 𝑛𝑛 𝑟𝑟 = ∫ 𝑑𝑑 3 𝑟𝑟2 ∫ 𝑑𝑑 3 𝑟𝑟3 … … ∫ 𝑑𝑑 3 𝑟𝑟 𝑁𝑁 |𝞇𝞇 𝑟𝑟, 𝑟𝑟2 , … 𝑟𝑟 𝑁𝑁 |2
n(r) uniquely determines 𝑉𝑉𝑒𝑒𝑒𝑒𝑒𝑒 .
𝑉𝑉𝑒𝑒𝑒𝑒𝑒𝑒 = ∫ 𝑣𝑣 𝑒𝑒𝑒𝑒𝑒𝑒 𝑟𝑟 𝑛𝑛 𝑟𝑟 𝑑𝑑𝑑𝑑
𝐸𝐸 𝑛𝑛 = 𝐹𝐹 𝑛𝑛 + ∫ 𝑣𝑣 𝑒𝑒𝑒𝑒𝑒𝑒 𝑟𝑟 𝑛𝑛 𝑟𝑟 𝑑𝑑𝑑𝑑
The total energy functional can be written as

9. 
Universal function F(n) is Independent of External
potential but it is unknown.

10. INPUT




INCAR
POSCAR
POTCAR
KPOINTS
OUTPUT









OUTCAR
OSCZICAR
CONTCAR
CHGCAR
EIGENVAL
WAVECAR
PROCAR
XDATCAR
DOSCAR

11. INCAR: Central Input file.
:Different parameters for different properties.
. POSCAR: Position of Ions
: Lattice Constant
.POTCAR : Psuedopotential from VASP
.KPOINTS: Kpoint meshes


12. 





For Binding Energy calculation, I have to
calculate single point Energy calculation.
I take Oxygen as an example.
Here I do spin Polarised calculation.
For single O atom, Input files are INCAR,
POSCAR, POTCAR, KPOINTS.
For O2 dimer, only POSCAR file is modified.
B.E =E(O2)-2*E(O)

13. INCAR
POSCAR
KPOINTS

14. POTCAR

15. FREE Energy value
for O Atom

16. 



Here all the Input files are same as those for
Oxygen Atom.
Only POSCAR File is slightly changed.
Here No. of atoms is 2
Hence two co-ordinate points are required for
describing the position of atoms in the
molecule.

18. Energy of Oxygen Molecule
Binding Energy = E (O2)-2*E(O)
= -9.83466139+3.96809746
= -5.86656393eV

19. Here I choose Cl2 dimer.

Input files : INCAR,POSCAR, POTCAR, KPOINTS

Open POSCAR file
Cl2 Molecule ! Comment line
1.00
!Length Unit in Angstrom
10.0 0.00 0.00
Lattice Vectors
0.00 10.0 0.00
0.00 0.00 10.0
2
No. of Atoms
Cartesian
0.00 0.00 0.00
Position of
Atoms
1.97 0.00 0.00


20. 





Now edit the POSCAR file and Change X-Co-ordinate of second
Cl atom to 1.99A
Save the file and run VASP
Record Energy value.
Repeat the Calculation for successive increase in bond length up
to 2.07A and record corresponding Energy values.
Plot the graph between Energy and bond Length.
The Length corresponds to minimum energy is the equilibrium
bond length.

21. 


Here I choose Cu atom in FCC phase.
Keep all INPUT files (INCAR,POSCAR,POTCAR,KPOINTS)
POSCAR File
Cu
3.55
0.5 0.5 0.0
0.0 0.5 0.5
0.5 0.0 0.5
1
Cartesian
000
Lattice vector in FCC
System

22. 




Edit POSCAR file and Change Lattice Constant to 3.60 A
Save the file and run the job and record energy
Repeat the calculation by successive increase in length up to 3.70A
and record all corresponding Energy values.
Plot the graph between energy with lattice constant.
The lattice constant corresponds to minimum energy is actual
lattice constant.

23. 



The silicon Crystal structure is FCC .
FCC primitive unit cell with 2 atoms in the
unit cell.
For band structure calculation first run selfconsistency calculation to get the charge
density.
Then fix the charge density and run a non self
consistency calculation for desired K points to
get band structure.

24. INCAR for SCF Calculation
For SCF calculation ICHARG
=2
For GGA
psuedopotential

25. POSCAR
For
FCC,
no. of
atoms
per
unit
cell

26. KPOINTS
For Automatic Mesh
Generation

27. 



POTCAR file is provided by VASP
Then run VASP
After job is completed, we get charge density in
CHGCAR file
To get band structure, run non-self consistence
calculation for each desired k points.

28. 



Input files are INCAR, POSCAR, POTCAR,
KPOINTS, CHGCAR.
INCAR and KPOINTS files will be modified.
In INCAR file, we change ICHARG=11
We modify KPOINTS file, to specify along
some high symmetry direction to calculate
energy.

29. Along each line, 10 kpoints
are calculated.
Reciprocal space

30. 




Run VASP
The above KPOINTS file instructs vasp to
calculate the Energy at each k point between L
point and Gamma point, gamma point and K
point.
Along each line 10 Kpoints are calculated.
In output, we find EIGENVAL file.
From this we find all information to plot band
structure.

31. EIGENVAL file
Kpoints
Energy of 8 bands
at that particular
energy point

32. 

Since energy of bands at each k points, we get
information about band structure.
I Plot band structure using MATLAB.

33. Band Structure of Silicon

34. 



Graphene is a 2-dimensional crystalline
allotrope of carbon.
In graphene, Carbon atoms are densely packed
in a regular hexagonal pattern.
It is one atom thick layer of graphite.
Input files INCAR, POSCAR, POTCAR,
KPOINTS

35. INPUT files for SCF Calculation for graphene
INCAR
POSCAR
KPOINTS

36. POTCAR

37. KPOINTS for Graphene Along high
symmetry line

38. Band Structure of Graphene

39. 


W.Kohn. L.J.Sham, physical rev.
140,A1133(1965)
H.J. Monkhrost and J.Pack, Phys. Rev.B
13,5188(1976)
W.Kohn,
A.D.Becke,R.G.Parr,J.Phys.Chem.1996, 100,
12974-12980